
1第八章傅里叶变换.188-1.傅里叶积分公式我们按照上面的分析方式(即令T→+cx-),由周期函数的傅里叶级数来推导非周期函数的傅里叶积分公式,这里只是形式推导,并不是严格的证明.有关严格证明可参考数学分析方面的相关教材将非周期函数f(t)看成是由周期函数(t)当T→×时转化米的,由(8.2)式与(8.3)式有f(t)= lim f-(t)fr(r)c mad)limFCL将间篇 a记为 Aw,节点 n。 记为 α,并由 T=2=,得wuAa1limf(t) =fr(t)ewdr.elaAu-2元/e这是一个和式的极限,按照积分定义,在一定条件下,上式可写为F() = J[f(r)e-mdt Jerda.(8.4)由此得到下面的定理定理8.2(傅氏积分定理)如果f(t)在(一α0,十0)上的任一有限区间满足秋氏条件,且在(一,十)上绝对可积(即If(t) /dt<十),则(8.4)式成立.在f()的间断点处,(8.4)式的左端应为[f(t+0)+ f(t-0)].称(8.4)式为傅里叶积分公式,简称傅氏积分。2.傅里叶变换从(8.4)式出发,令F(w) :f(t)e-mdt.(8.5)则有f(t) =I{*" F(o)erdo.(8. 6)2T
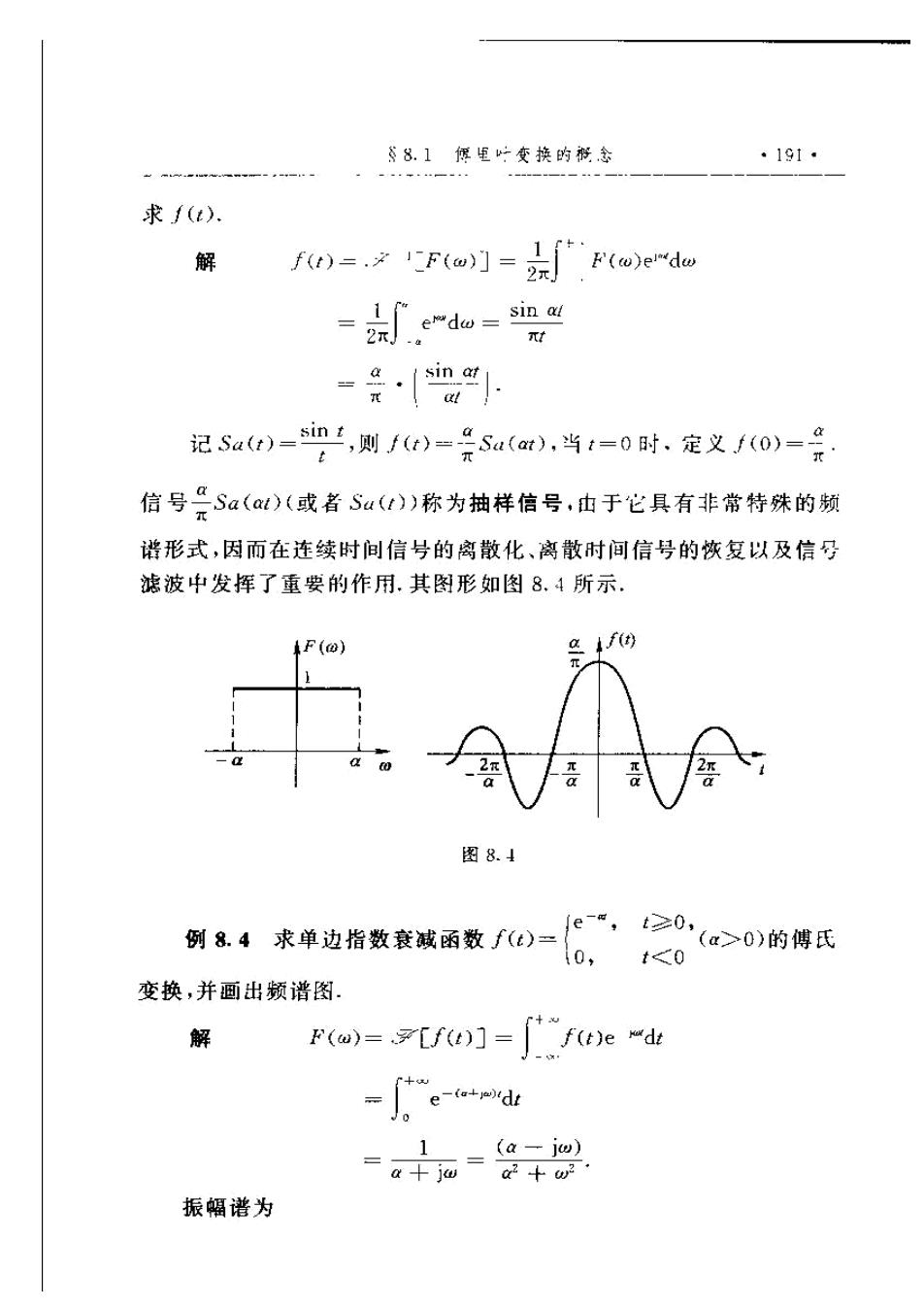
$8. 1您里听变换的概念.191.求f (t).f(1)=.21F(w)) =F(w)e"da)解sin αlemdw=2元元tin.esintaL,则f(t)二记Sa(t):Su(at),当t=0时,定义f(0)=t7信号~Sa(αt)(或者Su(t))称为抽样信号,由于它具有非常特殊的频谱形式,因而在连续时间信号的离散化、离散时间信号的恢复以及信号滤波中发挥了重要的作用,其图形如图8.4所示,αf(t)F(0)at02元元图8.4t0例8.4求单边指数衰减函数f()(α>0)的傅氏t<o10.变换,并画出频谱图解f(t)e mdtF(w)= Frf() =a+jadt(α - jo)1+jwa2+振幅谱为

:193:88.2单位脉冲函数(函数)x, x=0,(8. 8)p(r) = limp(r) =0,r0.显然,仅用(8.8)式这种“常规”的函数表述方式,并不能反映出质点本身的质量,必须附加一个条件p()d=m,为此我们需要引人一个新的函数,即所谓的单位脉冲函数,又称为狄拉克函数或者函数,38.2.1单位脉冲函数的概念及其性质依照上面的例子,我们可以简单地定义单位脉冲函数(t)是满足下面两个条件的函数:(1)当t#0时,8(t)=0;8(t)dt= 1.(2)这是由狄拉克给出一种直观的定义方式,按照此定义,则例8.5中的质点的密度函数为o(r)=mo()这里需要指出的是,上述定义方式在理$5e(0)论上是不严格的,它只是对函数的某种描述,事实上,函数并不是经典意义上的函数,而是一个广义函数,因此,关于函数的严格定义可参阅有关广义函数方面的书籍另外,函数在现实生活中也是不存在的,它是数学抽象的结果.有时入们将函数直观图8.6的理解为(t)=limo.(t),其中(t)是宽度为e高度为1/e的矩形脉冲函数(图8.6)下面我们不加证明地直接给出函数的几个基本性质,性质8.1设f(t)是定义在实数域R上的有界函数,且在1=0处连续,则?(t)f(t)dt=f(o),(8.9)一般地,若f(t)在t一点连续,则