
圆锥面方程 =±/x2+2cotα即2=α'(x+y2)(a = cotα)元a=时, cotα=1三α=4即圆锥面方程z2=x2+y(用得较多)vOz面上直线方程为y=zcotaZ绕y轴旋转所得曲面方程及图形y= ±/x2+z2 cotα即 = cot α(x +z)= a(x2+z) (a=cotα)17
圆锥面方程 cot 2 2 z = x + y 即 圆锥面方程 ( ) ( cot ) 2 2 2 2 即 z = a x + y a = a = 1时, cot = 1 4 = 2 2 2 z = x + y (用得较多) y = z cot 绕y轴旋转所得曲面方程及图形. cot ( ) 2 2 2 2 y = x + z ( ) 2 2 2 = a x + z (a = cot) y = cot 即 yOz 面上直线方程为 2 2 x + z O z x y
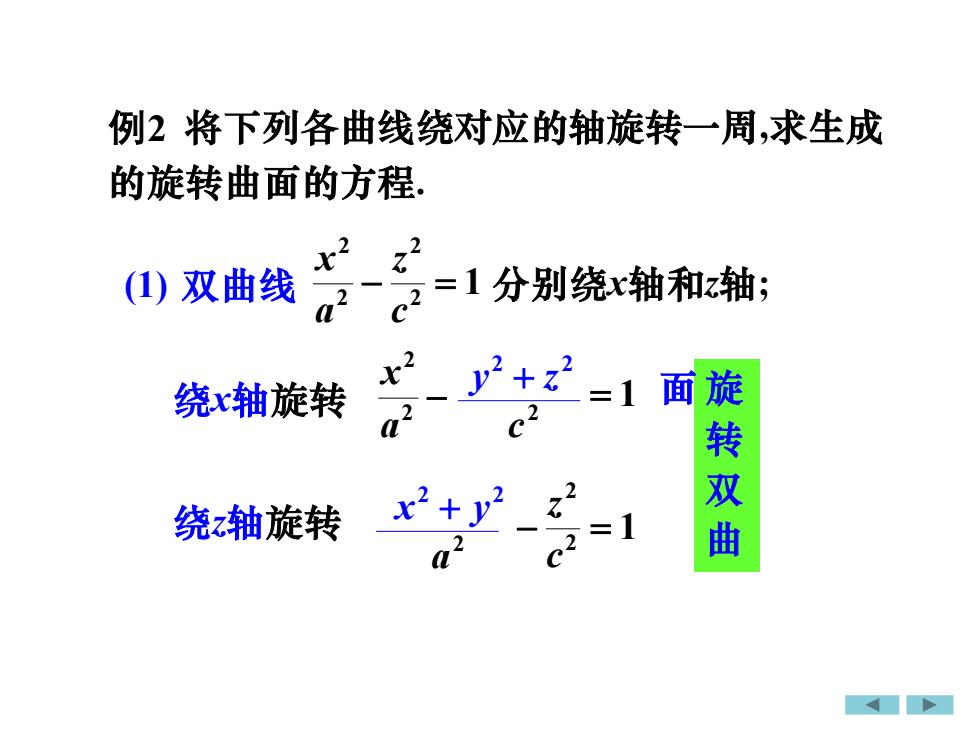
例2将下列各曲线绕对应的轴旋转一周,求生成的旋转曲面的方程22Nr1分别绕x轴和z轴(1) 双曲线2a2r+面旋转双曲绕x轴旋转22ca7绕轴旋转2Ca
将下列各曲线绕对应的轴旋转一周,求生成 的旋转曲面的方程. 1 2 2 − = c z 旋 转 双 曲 面 例2 (1) 双曲线 1 2 2 2 2 − = c z a x 分别绕x轴和z轴; 绕x轴旋转 绕z轴旋转 2 c 2 2 y + z −2 2 a x = 1 2 2 x + y 2 a

7.(2) yOz坐标面上的椭圆=1绕y轴和z轴;Ca+7旋转椭=1球绕y轴旋转面a27+绕轴旋转2(3)yOz坐标面上的抛物线2=2pz绕z轴x2 + y? = 2 pz旋转抛物面
绕y轴旋转 绕z轴旋转 1 2 2 2 2 2 = + + c x z a y 1 2 2 2 2 2 + = + c z a x y 旋 转 椭 球 面 x y 2 pz 2 2 + = 旋转抛物面 (2) 1 2 2 2 2 + = c z a y yOz坐标面上的椭圆 绕y轴和z轴; (3) yOz y 2 pz 2 坐标面上的抛物线 = 绕z轴

选择题方程(z-a)2=x2+y表示( B).(A)xOz平面上曲线(z-a)°=x绕y轴旋转所得曲面;(B)xOz平面上直线z一a=x绕z轴旋转所得曲面;(C)yOz平面上直线z一a=y绕y轴旋转所得曲面;(D)yOz平面上曲线(z-a)2= J"绕x轴旋转所得曲面
选择题 方程 B 2 2 2 (z − a) = x + y (A) xOz平面上曲线 绕y轴旋转所得曲面; 2 2 (z − a) = x (B) xOz平面上直线 z −a = x 绕z轴旋转所得曲面; (C) yOz平面上直线 z − a = y 绕y轴旋转所得曲面; (D) yOz平面上曲线 绕x轴旋转所得曲面. 2 2 (z − a) = y 表示( )