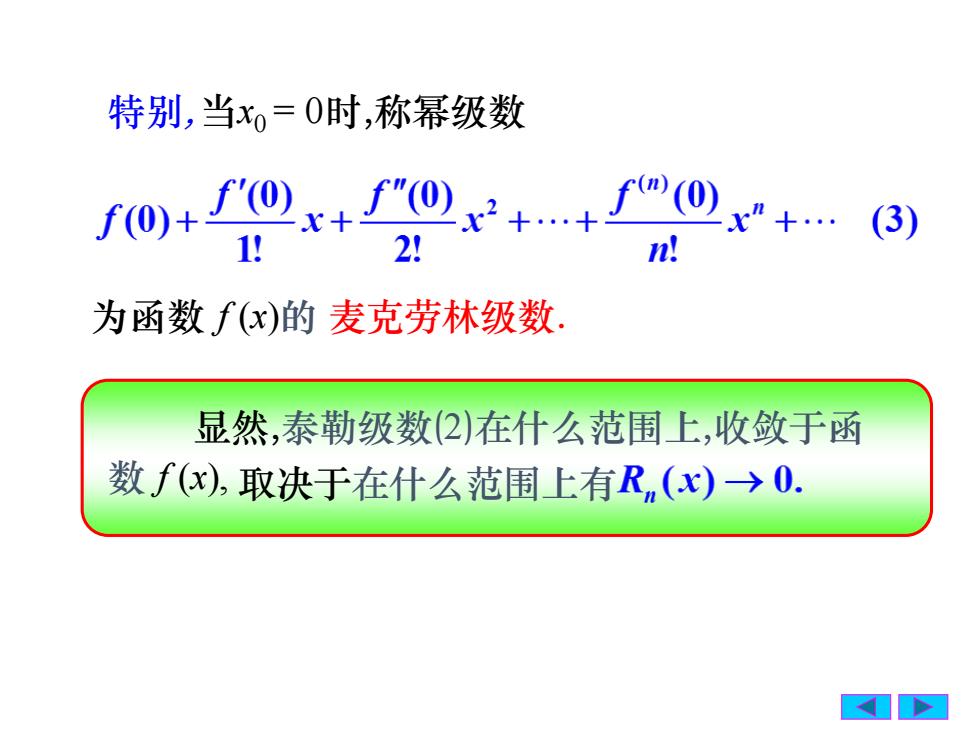
特别,当xo=0时,称幂级数f'(0)f"(0)(0)xn +...f(0)(3)X-1!2!n!为函数 f(x)的麦克劳林级数显然,泰勒级数2)在什么范围上,收敛于函数f(x),取决于在什么范围上有R,(x)→0
显然,泰勒级数(2)在什么范围上,收敛于函 数 f (x), 特别, 为函数 f (x)的 麦克劳林级数. 取决于在什么范围上有 当x0 = 0时,称幂级数

定理1 f(x)在点x,处泰勒级数在U(x)内收敛于f(x) 在U(x)内lim R,(x)=0.n-0证必要性设f(x)能展开为泰勒级数(xoN-x) + R,(x): f(x)=i!i=0: R,(x) = f(x)- Sn+i(x), : limSn+1(x) = f(x)n>00:. lim R,(x) =lim[f(x) - Sn+1(x) = 0 n→>0n→A
证 必要性 ( ) ( ) ! ( ) ( ) 0 0 0 ( ) x x R x i f x f x n i n i i = − + = ( ) ( ) ( ), Rn x = f x − sn+1 x 设f (x)能展开为泰勒级数, lim ( ) ( ) sn 1 x f x n + = → = → lim R (x) n n lim[ ( ) ( )] f x sn 1 x n + → − = 0; 定理1 f (x)在点x0 处泰勒级数在U(x0 )内 收敛于f (x) ( ) lim ( ) 0. 0 = → U x Rn x n 在 内

设 lim R,(x) = 0充分性n→: f(x) -Sn+i(x) = R,(x),:. lim[f(x) - Sn+(x)]= lim R, (x)= 0.n>n即 lim Sn+(x)= f(x),n>00::f(x)的泰勒级数收敛于f(x)
充分性 ( ) ( ) ( ), f x − sn+1 x = Rn x lim[ ( ) ( )] f x sn 1 x n + → − lim R (x) n n→ = = 0, lim ( ) ( ), sn 1 x f x n + = → 即 f (x)的泰勒级数收敛于 f (x). lim ( ) = 0 → R x n n 设

定理2(函数幂级数展开的唯一性如果函数f(x)在U(x)内可展为幂级数8f(x)=Eaan(x-xo)",n=0(n)(xo)则其系数(n = 0,1,2,..a11n规定: 0!=1, f(0)(x)= f(x)证由于幂级数在收敛区间内可逐项微分,于是f(x)=a, +a,(x-x.)+...+a,(x-x)" +..A
证 f (x) = a0 + a1 (x − x0 ) ++ an (x − x0 ) n + 由于幂级数在收敛区间内可逐项微分, 定理2(函数幂级数展开的唯一性) 如果函数f (x)在U(x0 )内可展为幂级数 则其系数 ( ) ( ) , 0 0 n n f x = an x − x = 于是 规定:0!= 1, ( ) ( ). 0 0 (0) f x = f x (n = 0,1,2, )

f'(x) = a, + 2az(x-x)+...+na,(x -x.)n-1 + .f"(x) = 2!az + 3.2as(x -x)+...+ n(n-1)a,(x -x.)n-2 + .f(n)(x) = n!a, +(n+1)n...3.2an+i(x-x,)+ :今即得x= Xo(n = 0,1,2, -)泰勒系数(xo)n!泰勒系数是唯一的,所以,f(β的展开式是唯一的
f (n) (x) = n!an + (n + 1)n3 2an+1 (x − x0 ) + , 令 x = x0 泰勒系数是唯一的, f (x) = a1 + 2a2 (x − x0 ) ++ nan (x − x0 ) n−1 + 泰勒系数 ( ) 2! 3 2 ( ) ( 1) ( ) , 2 f x = a2 + a3 x − x0 ++ n n − an x − x0 n− + 即得 所以, f (x)的展开式是唯一的