
2、单调性 Vx1,x2∈I,x1<x2时, 若f(x)<f(x2),称f(x)为I上的单调增函数, 若f(x)>f(x2),称f(x)为I上的单调减函数 南阳师范学院数学与统计学院高等数学教研室高等数学课件
2、 单调性 ,, 21 xx I 21 xx 时, ,)()( 1 2 若 xfxf 称 f x)( 为 I 上的 ,)()( 1 2 若 xfxf 称 f x)( 为 I 上的 单调增函数 ; 单调减函数 . 南阳师范学院数学与统计学院高等数学教研室高等数学课件
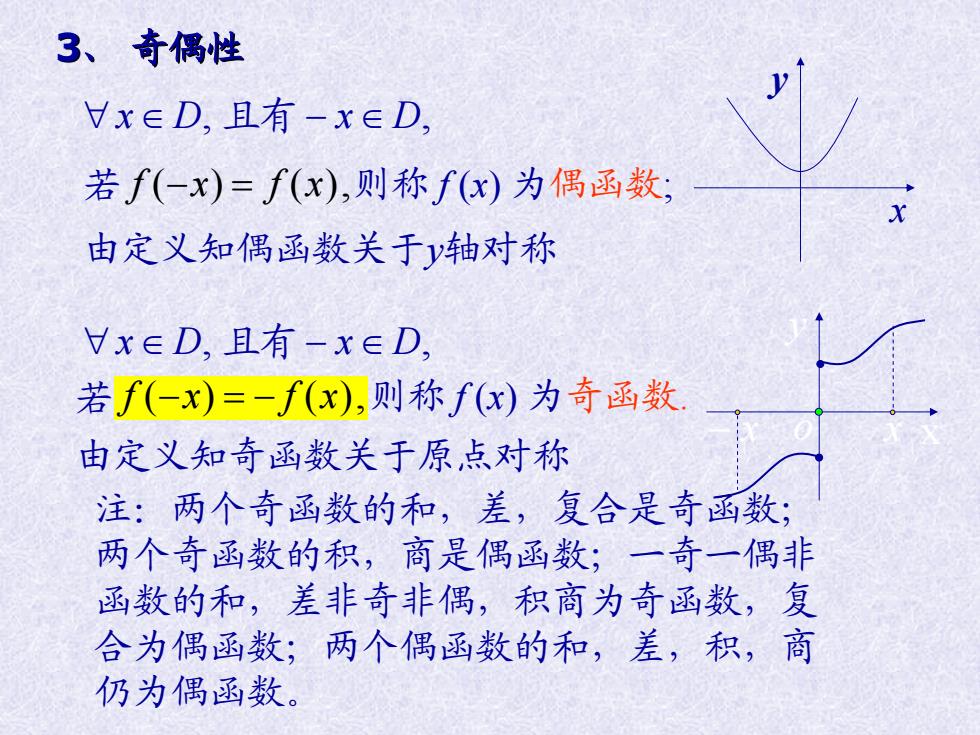
3、奇偶性 Vx∈D,且有-x∈D, 若f(-x)=f(x),则称f(x)为偶函数; 由定义知偶函数关于y轴对称 Hx∈D,且有-x∈D 若f(-x)=-f(x),则称f(x)为奇函数 由定义知奇函数关于原点对称 注:两个奇函数的和,差,复合是奇函数; 两个奇函数的积,商是偶函数;一奇一偶非 函数的和,差非奇非偶,积商为奇函数,复 合为偶函数;两个偶函数的和,差,积,商 仍为偶函数
x D, 且有 x D, 若 f x f x ,)()( 则称 f (x) 为偶函数; 若 f x f x ,)()( 则称 f (x) 为奇函数. x y x o x 3、 奇偶性 由定义知偶函数关于y轴对称 x y x D, 且有 x D, 由定义知奇函数关于原点对称 注:两个奇函数的和,差,复合是奇函数; 两个奇函数的积,商是偶函数;一奇一偶非 函数的和,差非奇非偶,积商为奇函数,复 合为偶函数;两个偶函数的和,差,积,商 仍为偶函数

4、周期性 设函数x)的定义域为D,如果存在一个正数1,使 得对于任一x∈D,有x±I∈D,且 f(x±)=∫(x)则称f(x)为周期函数,称1为周期 (一般指最小正周期) 注意:周期函数不一定存在最小正周期 例如:常数函数(x)=C 1,x为有理数 或狄里克雷函数f(x)= 0,x为无理数 注意:最小正周期是函数图象出现重复的最小距离 南阳师范学院数学与统计学院高等数学教研室高等数学课件
Dx ,有 lx D, f lx f x)()( 则称 xf )( 为周期函数 , 且 称 l 为周期 ( 一般指最小正周期 ). 注意: 周期函数不一定存在最小正周期 . f )( Cx 4、 周期性 设函数f(x)的定义域为D,如果存在一个正数l,使 得对于任一 例如:常数函数 狄里克雷函数 f x)( x 为有理数 x 为无理数 ,1 ,0 或 注意: 最小正周期是函数图象出现重复的最小距离. 南阳师范学院数学与统计学院高等数学教研室高等数学课件

(三)反函数与复合函数 1、反函数的概念及性质 若函数∫:D→f(D)为单射则存在逆映射 f广:f(D)-→D 称此映射f为f的反函数 习惯上,y=f(x),x∈D的反函数记成 y=(x),x∈f(D) 南阳师范学院数学与统计学院高等数学教研室高等数学课件
1、 反函数的概念及性质 若函数 f Df D)(: 为单射, 则存在逆映射 DDff )(: 1 习惯上, y f ,)( xx D 的反函数记成 )(,)(1 Dfxxfy 称此映射 1 f 为 f 的反函数 . (三) 反函数与复合函数 反函数与复合函数 南阳师范学院数学与统计学院高等数学教研室高等数学课件

性质: 1)y=f(x)单调递增(减)其反函数y=∫(x)存在 且也单调递增(减) 2)函数y=f(x)与其反函数 yy=f(x) y=∫(x)的图形关于直线 P=x Q(b,a) y=x对称 y=f(x) 如图: 指数函数y=e',x∈(-o,+∞) 互为反函数, 对数函数y=lnx,x∈(0,+oo) 它们都单调递增,其图形关于直线y=x对称 南阳师范学院数学与统计学院高等数学教研室高等数学课件
(减) 其反函数 (减) . 1) y=f (x) 单调递增 ,)( 1 xfy 存在 且也单调递增 2) 函数 y f x)( 与其反函数 )(1 xfy 的图形关于直线 xy 对称 . xfy )( )(1 xfy y x abQ ),( baP ),( x y o 如图: xey ),(, x 对数函数 y xx ),0(,ln 互为反函数 , 它们都单调递增, 其图形关于直线 xy 对称 . 指数函数 性质: 南阳师范学院数学与统计学院高等数学教研室高等数学课件