
94年 (1)己知A、B两个事件满足条件P(AB)=P(AB),且P(A)p, 则P(B)= 。(3分)》 (2)设相互独立的两个随机变量X,Y具有同一分布律,且X的分布律为 x01 P 22 则随机变量z=max{X,Y的分布律为 。(3分) (3)已知随机变量X,Y分别服从正态分布N1,32),N(0,42),且X,Y的相关系数 (1)求Z的数学期望EZ和方差DZ: (2)求X与Z的相关系数P: (3)问X与Z是否相互独立?为什么?(满分6分) 95年 (1)设X表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则X 的数学期望E(X2)=_ 2)设X,y为两个随机变量,且PX≥0,Y≥0)=,P(X≥0y=Py≥0)= 则P{max(X,Y≥0}= (3)设随机变量X的概率密度为 f()=fe x20 10,x<0 求随机变量Y=ex的概率密度了,(y)。(6分) 96年 1,设工厂A和工厂B的产品的次品率分别为1%和2%,现从由A厂和B厂的产品分 别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品是A 厂生产的概率是 _。(3分) 2.设5,7是两个相互独立且均服从正态分布N0,方)的随机变量,则B05-”》 。(3分)
94 年 (1)已知 A、B 两个事件满足条件 P(AB)=P( A B ),且 P(A)=p, 则 P(B)= 。(3 分) (2)设相互独立的两个随机变量 X Y, 具有同一分布律,且 X 的分布律为 X 0 1 P 1 2 1 2 则随机变量 z X Y = max , 的分布律为 。(3 分) (3)已知随机变量 X Y, 分别服从正态分布 2 2 N N (1,3 ) , (0,4 ) ,且 X Y, 的相关系数 1 2 xy = − ,设 3 2 X Y z = + , (1)求 Z 的数学期望 EZ 和方差 DZ ; (2)求 X 与 Z 的相关系数 xz ; (3)问 X 与 Z 是否相互独立?为什么?(满分 6 分) 95 年 (1)设 X 表示 10 次独立重复射击命中目标的次数,每次射中目标的概率为 0.4,则 2 X 的数学期望 2 E X( ) = 。 (2)设 X Y, 为两个随机变量,且 3 4 0, 0 , 0 0 7 7 P X Y P X P Y = = = , 则 P X Y max( , ) 0 = 。 (3) 设随机变量 X 的概率密度为 = − 0, 0 0 ( ) x e x f x x X 求随机变量 X Y = e 的概率密度 f (y) Y 。(6 分) 96 年 1. 设工厂 A 和工厂 B 的产品的次品率分别为 1%和 2%,现从由 A 厂和 B 厂的产品分 别占 60%和 40%的一批产品中随机抽取一件,发现是次品,则该次品是 A 厂生产的概率是 。(3 分) 2. 设 , 是两个相互独立且均服从正态分布 N(0, 2 1 )的随机变量,则 E(| − |) = 。(3 分)

3.设5,”是相互独立且服从同一分布的两个随机变量,已知的分布律为 P5=)=i=l2,3又设X=ma5,y=min5, (1)写出二维随机变量(X,Y)的分布律: 2 3 1 2 3 (2)求EX.(共6分) 97年 1.袋中有50个乒乓球,其中20个是黄球,30个是白球。今有两人依次随机地从袋 中各取一球,取后不放回,则第2个人取得黄球的概率是」 。(3分 2设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X-2Y的方差是 (A)8 (B)16 (C)28 (D)4413分1 3.从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是 相互独立的,并且概率都是子。设X为途中遇到红灯的次数,求随机变量X的分布律、分 布函数和数学期望。(7分) 4.设总体X的概率密度为 f)=0+Ir”0<r<1 0,其他 其中0>-1是未知参数X,X2,…,X是来自总体X的一个容量为n的简单随机样本,分 别用矩估计法和极大似然估计法求0的估计量。(5分) 98年 1.(3分)设A,B是两个随机事件,且0PM),P(BP0,P(B1A=PB1A),则必有 (A)P (AB)=P(A B) (B)P (AIB)#P(A [B) (C)P (AB)=P(A)P (B) (D)P (AB)#P(A)P(B) 2.(6分)设两个随机变量X、Y相互独立,且都服从均值为0、方差为的正态分 布,求XY的方差。 3.(4分)从正态总体N(3.4,62)中抽取容量为n的样本,如果要求其样本均值位于
3.设 , 是相互独立且服 从同一分布的两 个随机变量,已 知 的分布律为 1 ( ) , 1,2,3, max( , ), min( , ). 3 P i i X Y = = = = = 又设 (1) 写出二维随机变量(X,Y)的分布律; X Y 1 2 3 1 2 3 (2) 求 EX。(共 6 分) 97 年 1. 袋中有 50 个乒乓球,其中 20 个是黄球,30 个是白球。今有两人依次随机地从袋 中各取一球,取后不放回,则第 2 个人取得黄球的概率是 。(3 分) 2.设两个相互独立的随机变量 X 和 Y 的方差分别为 4 和 2,则随机变量 3X-2Y 的方差是 ( ) (A)8 (B)16 (C)28 (D)44 [3 分] 3. 从学校乘汽车到火车站的途中有 3 个交通岗,假设在各个交通岗遇到红灯的事件是 相互独立的,并且概率都是 5 2 。设 X 为途中遇到红灯的次数,求随机变量 X 的分布律、分 布函数和数学期望。(7 分) 4. 设总体 X 的概率密度为 + = 0, 其他 ( 1) 0 1 ( ) x x f x 其中 X X Xn 1 . , , , − 是未知参数 1 2 是来自总体 X 的一个容量为 n 的简单随机样本,分 别用矩估计法和极大似然估计法求 θ 的估计量。(5 分) 98 年 1.(3 分)设 A、B 是两个随机事件,且 0<P(A)<1, P(B)>0, P(B | A)=P(B | A ),则必有 (A)P(A | B)= P( A |B) (B)P(A | B)≠P( A |B) (C)P(AB)= P(A)P(B) (D)P(AB)≠P(A) P(B) 2.(6 分) 设两个随机变量 X、Y 相互独立,且都服从均值为 0、方差为 2 1 的正态分 布,求|X-Y|的方差。 3.(4 分) 从正态总体 (3.4,6 ) 2 N 中抽取容量为 n 的样本,如果要求其样本均值位于
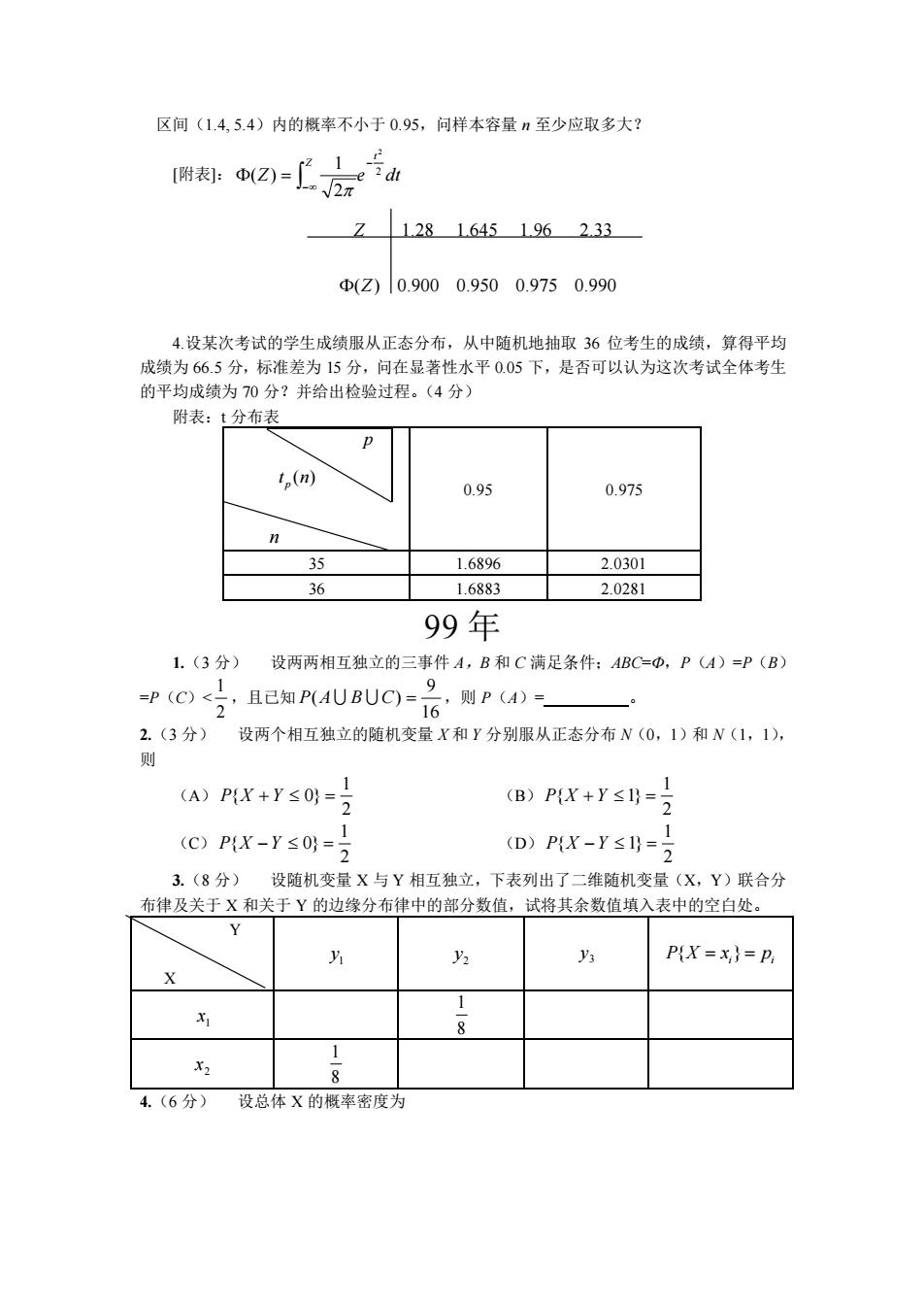
区间(1.4,5.4)内的概率不小于0.95,问样本容量n至少应取多大? 712816451962.33 d(Z)0.9000.9500.9750.990 4.设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均 成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为这次考试全体考生 的平均成绩为70分?并给出检验过程。(4分) 附表 t分布表 tn(n)) 0.95 0.975 1.689 2.030 36 1.6883 2.0281 99年 1.(3分) 设两两相互独立的三事件A,B和C满足条件:ABC=D,P(M)=P(B) =P(宁且已知4UBU=G则P- 2.(3分)设两个相互独立的随机变量X和y分别服从正态分布N(0,1)和N(1,1), (A)P(X+Y50)= 2 (B)P(X+Ys=1 CPr-rs明= (D)PX-Y≤I=2 3.(8分)设随机变量X与Y相互独立,下表列出了二维随机变量(X,Y)联合分 布律及关于X和关于Y的边缘分布律中的部分数值,试将其余数值填入表中的空白处 P(X=x)=P 1 x 8 8 4.(6分)设总体X的概率密度为
区间(1.4, 5.4)内的概率不小于 0.95,问样本容量 n 至少应取多大? [附表]: Z e dt t Z 2 2 2 1 ( ) − − = 1.28 1.645 1.96 2.33 ( ) 0.900 0.950 0.975 0.990 Z Z 4.设某次考试的学生成绩服从正态分布,从中随机地抽取 36 位考生的成绩,算得平均 成绩为 66.5 分,标准差为 15 分,问在显著性水平 0.05 下,是否可以认为这次考试全体考生 的平均成绩为 70 分?并给出检验过程。(4 分) 附表:t 分布表 p ( ) p t n n 0.95 0.975 35 1.6896 2.0301 36 1.6883 2.0281 99 年 1.(3 分) 设两两相互独立的三事件 A,B 和 C 满足条件;ABC=Ф,P(A)=P(B) =P(C)< 2 1 ,且已知 16 9 P(A B C) = ,则 P(A)= 。 2.(3 分) 设两个相互独立的随机变量 X 和 Y 分别服从正态分布 N(0,1)和 N(1,1), 则 (A) 2 1 P{X + Y 0} = (B) 2 1 P{X + Y 1} = (C) 2 1 P{X −Y 0} = (D) 2 1 P{X −Y 1} = 3.(8 分) 设随机变量 X 与 Y 相互独立,下表列出了二维随机变量(X,Y)联合分 布律及关于 X 和关于 Y 的边缘分布律中的部分数值,试将其余数值填入表中的空白处。 Y X 1 y 2 y 3 y { } P X x p = = i i 1 x 8 1 2 x 8 1 4.(6 分) 设总体 X 的概率密度为

o o. 0-x)0<x<0 其他 X,X2,,X是取自总体X的简单随机样本。 (1)求0的矩估计量0: (2)求0的方差D(⊙. 00年 1.(3分)设两个相互独立的事件A和B都不发生的概率为。,A发生B不发生的 概率与B发生A不发生的概率相等,则P(A)= 2.(3分)设二维随机变量(X,Y)服从二维正态分布,则随机变量 5=X+与n=X-Y不相关的充分必要条件为 (A)E(X)=E(Y) (B)E(X2)-[E(X)]2=E(Y2)-[E(Y)]2 (C)E(X2)=EY2) (D)E(X2)+[E(X)]2=EY2)+[EY) 3.(8分)某流水生产线上每个产品不合格的概率为风0<<1),各产品合格与否相互 独立,当出现一个不合格产品时即停机检修。设开机后第一次停机时已生产了的产品个数为 X,求E(X)和DX) 4.(6分) 设某种元件的使用寿命X的概率密度为 0)=f2e 0.x≤0 其中0为未知参数。又设x1,x2,,xn是X的一组样本观测值,求参数0的最大似然估计 值。 01年 13分) 将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数 则X和y的相关系数等于 (A)-1 (B)0 (D)1 [1
− = 其他 ( ) 0, ( ) 0 6 3 x x x f x X X Xn , , , 1 2 是取自总体 X 的简单随机样本。 (1) 求 θ 的矩估计量 ˆ ; (2) 求 ˆ 的方差 ˆ D( ) 。 00 年 1.(3 分) 设两个相互独立的事件 A 和 B 都不发生的概率为 9 1 ,A 发生 B 不发生的 概率与 B 发生 A 不发生的概率相等,则 P(A)= 。 2.(3 分) 设 二 维 随 机 变 量 ( X , Y ) 服 从 二 维 正 态 分 布 , 则 随 机 变 量 = X +Y与 = X −Y 不相关的充分必要条件为 (A) E(X ) = E(Y) (B) 2 2 2 2 E(X ) −[E(X)] = E(Y ) −[E(Y)] (C) ( ) ( ) 2 2 E X = E Y (D) 2 2 2 2 E(X ) +[E(X)] = E(Y ) +[E(Y)] [ ] 3.(8 分) 某流水生产线上每个产品不合格的概率为 p(0<p<1),各产品合格与否相互 独立,当出现一个不合格产品时即停机检修。设开机后第一次停机时已生产了的产品个数为 X,求 E(X)和 D(X)。 4.(6 分) 设某种元件的使用寿命 X 的概率密度为 = − − x e x f x x 0, 2 ( ; ) 2( ) 其中 θ>0 为未知参数。又设 x1 , x2 , , xn是X 的一组样本观测值,求参数 θ 的最大似然估计 值。 01 年 1.(3 分) 将一枚硬币重复掷 n 次,以 X 和 Y 分别表示正面向上和反面向上的次数, 则 X 和 Y 的相关系数等于 (A)-1 (B)0 (C) 2 1 (D)1 [ ]

2.(3分)设随机变量X的方差为2,则根据切比雪夫不等式有估计 PIX-E(X)E2}≤ 3.(7分)设总体X~N(4,σ2)(o>0),从该总体中抽取简单随机样本 XXk之2),其样术曲均货不-品空。束烧计# Y=立(X,+X-2y的数学期塑E(. 4.(7分)设某班车起点站上客人数X服从参数为(1>0)的泊松分布,每位乘客 在中途下车的概率为p0<P<),且中途下车与否相互独立。以y表示在中途下车的 人数,求: (1)在发车时有n个乘客的条件下,中途有m人下车的概率: (2)二维随机变量(X,)的概*分布。 02年 1.(3分)设随机变量X服从正态分布N(4,(g>0),且二次方程 y广+4y+X=0无实根的概率为则“= 2.(3分)设X,和X2是任意两个相互独立的连续型随机变量,它们的概率密度 分别为f(x)和时(x),分布函数分别为E(x)和E(x),则 (A)f(x)+f5(x)必为某一随机变量的概率密度: (B)f(x)·,(x)必为某一随机变量的概率密度: (C)F(x)+F(x)必为某一随机变量的分布函数: (D)F(x)·F()必为某一随机变量的分布函数 (I 3.(7分)设随机变量X的概率密度为 f)=os克0sx≤ 「1 01 其他 对X独立地重复观察4次,用Y表示观察值大于号的次数,求Y的数学期望
2.(3 分) 设 随 机 变 量 X 的 方 差 为 2 , 则 根 据 切 比 雪 夫 不 等 式 有 估 计 P{| X − E(X ) | 2} 。 3.(7 分) 设总体 ~ ( , )( 0) 2 X N , 从 该 总 体 中 抽 取 简 单 随 机 样 本 , , , ( 2) X1 X2 X2n n , 其 样 本 的 均 值 = = n i Xi n X 2 1 , 2 1 求统计量 = = + + − n i Y Xi X n i X 1 2 ( 2 ) 的数学期望 E(Y)。 4.(7 分)设某班车起点站上客人数 X 服从参数为 ( 0) 的泊松分布,每位乘客 在中途下车的概率为 p p (0 1) ,且中途下车与否相互独立。以 Y 表示在中途下车的 人数,求: (1)在发车时有 n 个乘客的条件下,中途有 m 人下车的概率; (2)二维随机变量 ( , ) X Y 的概率分布。 02 年 1.(3 分) 设随机变量 X 服 从 正 态 分 布 ( , )( 0) 2 N ,且二次方程 4 0 2 y + y + X = 无实根的概率为 2 1 ,则 = 。 2.(3 分) 设 X1和X2 是任意两个相互独立的连续型随机变量,它们的概率密度 分别为 ( ) ( ) 1 2 f x 和f x ,分布函数分别为 ( ) ( ) 1 2 F x 和F x ,则 (A) ( ) ( ) 1 2 f x + f x 必为某一随机变量的概率密度; (B) ( ) ( ) 1 2 f x • f x 必为某一随机变量的概率密度; (C) ( ) ( ) 1 2 F x + F x 必为某一随机变量的分布函数; (D) ( ) ( ) 1 2 F x • F x 必为某一随机变量的分布函数。 [ ] 3.(7 分) 设随机变量 X 的概率密度为 = 0 其他 , 0 2 cos 2 1 ( ) x x f x 对 X 独立地重复观察 4 次,用 Y 表示观察值大于 3 的次数,求 2 Y 的数学期望