
30 一、《高等数学》(第七版)上册习题全解 所以当x+0时,(1-cosx)2是比sin2x高阶的无穷小 四3当x一1时,无穷小1-x和(1)1-2,(2)(1-2)是否同阶,是否等价? 解(臣产+1+4+兮.同阶,不等价 1-x 1 1-x (2121+5+x1一1).同阶.等价 24.证明:当x→0时,有 (1)arctan x~x; (2)-1号 证(1)令x=tant,即t=arctan x,当x0时,t→0. 因为 所以 aretan x-x(x→0). (2)因为 (2si2. x sin2号 所以 ex-1-(0 四5.利用等价无穷小的性质,求下列极限: 2)为正数 (3)lman二n sin x -tan x sin x (4)+1)(1+n- 解(0=2经=2 0,n>m, e)急g÷ 1,n=m, lo.n<m

第一章函数与极限 x2 =子号 注在作等价无穷小的代换求极限时,可以对分子或分母中的一个或若干个因子 作代换,但不能对分子或分母中的某个加项作代换.例如,本题中若将分子中的nx、 six均换成x,那么分子成为0,得出极限为0,这就导致错误的结果。 sin a -tan x (4)+2-1)(+mx-1) 1- =im2 =-3. 6 四6.证明无穷小的等价关系具有下列性质: (1)a~a(自反性); (2)若a~B,则B~a(对称性); (3)若a~B,B-y,则a~y(传递性). 证(因为m名=1,所以a-a: (2)因为a~B,即m合=1,所以im8=1,即B-a: (3)因为a-B,8-y,即1m音=1,m号=1.所以 m号=im(合·)=imgm号=1,即ax 习题1-8 函数的连续性与间断点 四1.设y=(x)的图形如图1-11所示,试指出(x)的全部间断点,并对可去间断点 补充或修改函数值的定义,使它成为连续点 图1-11
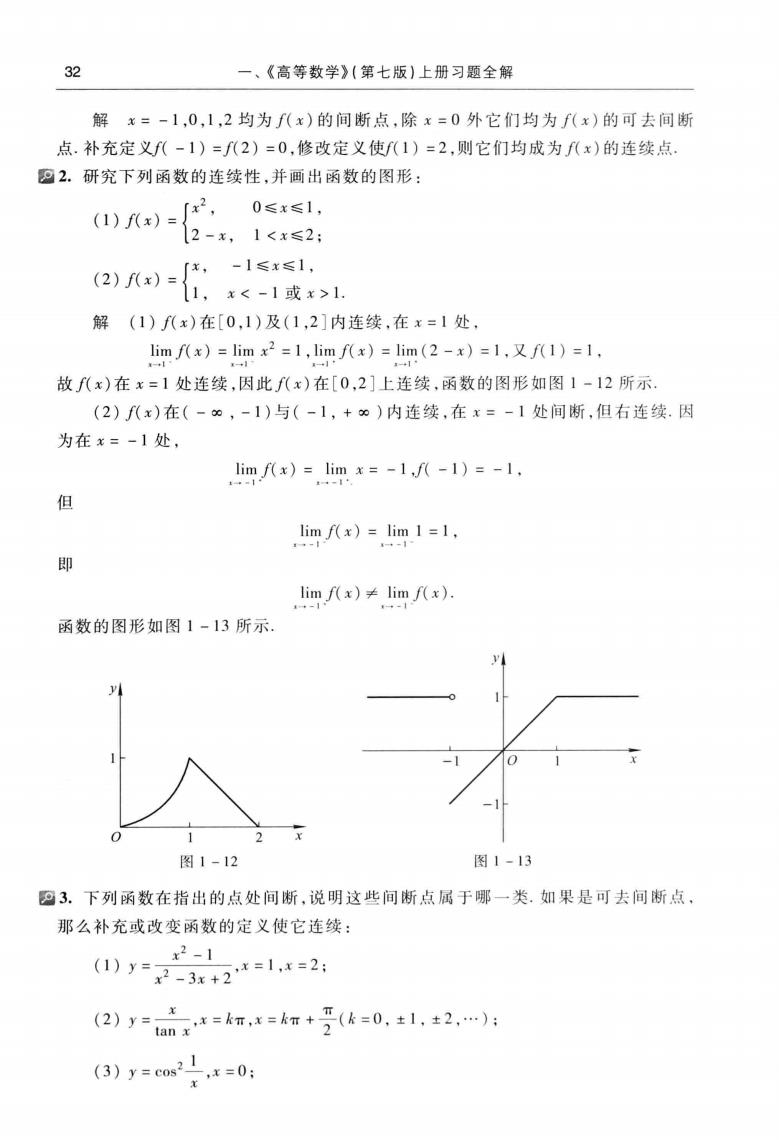
一、《高等数学》(第七版)上册习题全解 解x=-1,0,1,2均为f(x)的间断点,除x=0外它们均为f(x)的可去间断 点.补充定义f(-1)=八2)=0,修改定义使f(1)=2,则它们均成为f八x)的连续点. 22.研究下列函数的连续性,并画出函数的图形: 0≤x≤1, 12-x,1<x≤2: -1≤x≤1, 20=:1度 解(1)f八x)在[0,1)及(1,2]内连续,在x=1处. lim f(x)lim x2=1,lim f(x)lim(2-x)=1,f(1)=1, 故f(x)在x=1处连续,因此f(x)在[0,2]上连续,函数的图形如图1-12所示 (2)(x)在(-∞,-1)与(-1,+)内连续,在x=-1处间断,但右连续.因 为在x=-1处, limf八x)=limx=-l,f八-1)=-1. 但 lim/(x)=lim 1=1. 即 limf八x)≠limf(x). 函数的图形如图1-13所示. 图1-12 图1-13 ©3.下列函数在指出的点处间断,说明这些间断点属于娜一类.如果是可去间断点 那么补充或改变函数的定义使它连续: x2-1 0y-3+2=1=2 (2)ynx*=km,=km+受(k=0,±1,2,.:

第一章函数与极限 33 ( x=1. 解(1)对x=1,因为f(1)无定义,但 2-2 x2-1 所以,x=1为第一类间断点(可去间断点),重新定义函数: x2-1 ()=2-3x+21,2, 【-2, x=1, 则(x)在x=1处连续. 因为imf八x)=x,所以x=2为第二类间断点(无穷间断点). (2)对=0,因为0)无定义,=四支=1,所以=0为第一类间断点 (可去间断点),重新定义函数: (x)= 1, x=0 则(x)在x=0处连续. 对x=k知(k=士l,士2,.),因为im。=0,所以x=m(k=士1,士2,.)为 第二类间断点(无穷间断点). 对=如+受ke2,因为0,而函数在如+受处无定义,所以 m+牙(k∈Z)为第一类间断点(可去间断点),重新定义函数: lan x xkm,km+是 (x)= (k∈Z) 0,x=km+牙 则人(x)在x=m+(keZ)处连续。 (3)对x=0,因为mcms2及1imeo2均不存在,所以x=0为第二类间断点 (4)对x=1,因为1im/(x)=lim(3-x)=2,limf(x)=lim(x-1)=0,即左、右 极限存在,但不相等,所以x=1为第一类间断点(跳跃间断点). 注在讨论分段函数的连续性时,在函数的分段点处,必须分别考虑函数的左 连续性和右连续性,只有函数在该点既左连续,又右连续,才能得出函数在该点

一、《高等数学》(第七版)上册习题全解 连续, 4。讨论函数八)m的连续性,若有间断点,则判别其类型 袋 w尝-0 r-x,1x1>1, x,x<1. 在分段点x=-1处,因为 lim f(x)lim (-x)=1, lim八x)=limx=-l. limf(x)≠limf(x), 所以x=-】为第一类间断点(跳跃间断点). 在分段点x=1处,因为 limf八x)=limx=l, limf(x)lim(-x)=-1. limf(x)≠limf(x), 所以x=1为第一类间断点(跳跃间断点). ②5.下列陈述中,哪些是对的,哪些是错的?如果是对的,说明理由:如果是错的,试 给出一个反例 (1)如果函数f八x)在a连续,那么1f(x)I也在a连续: (2)如果函数1f(x)1在a连续,那么f(x)也在a连续. 解(1)对.因为 11f(x)1-lfa)ll≤1fx)-f(a)1→0(x一a) 所以If(x)1也在a连续. (2)错.例如 )={1,x≥0, 1-1,x<0, 则I八x)1在x=0处连续,而八x)在x=0处不连续, 四6.证明:若函数f八x)在点o连续且f八(xo)≠0,则存在x0的某一邻域U(x0),当 x∈U(xo)时,f八x)≠0. 证若/(o)>0,因为f(x)在连线,所以取e=(0)>0,38>0,当xe U(0,6)时,有x)-o)1<子0).即 0<2o)<x)<2o