
第五节 条件概率 一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式
一、条件概率 二、乘法定理 三、全概率公式与贝叶斯公式 第五节 条件概率

一、 条件概率 10引例 例1:将一枚硬币抛掷两次,观察正反两方面的情况,设 A:“至少有一次为正”,B:“两次掷出同一面”. 求已知事件A已经发生的条件下事件B发生的概率P(BA) 分析:样本空间为S={HH,HT,TH,TT} A-HH,HT,TH B=HH,TT,AB=(HH, P4=PAB)=B)-=2 新的样 事件A已经发生的条件下,所有可能的结果发A 本空间 尚方夹藏会式计不杂八利器 P(AB) P(A) 注意:P(B)=≠P(B1A)
3 ( ) , 4 P A = 例1: 将一枚硬币抛掷两次,观察正反两方面的情况,设 A: “至少有一次为正”, B:“两次掷出同一面”. 求已知事件A 已经发生的条件下事件B 发生的概率P(B|A). 分析: 事件A 已经发生的条件下, P B( ) 1 4 3 4 = ( ) ( ) P AB P A = 1 0 引例 一、条件概率 1 ( ) , 4 P AB = 1 = 2 P B A ( | ) 1 3 由古典概率公式计算得 P B A ( | ) = 所有可能的结果为A . 样本空间为S HH HT TH TT = , , , A HH HT TH = , , , B HH TT = , , AB HH = , 注意: 1 ( ) , 2 P B = 新的样 本空间
对于古典概型问题,设试验E的样本空间为S={e1,e2,.,en, 事件A的容量为m,AB的容量为k, 由古典概率得P(4-,P4B)-分 k P(BA)= A k B S P(BIA)= kk/n m m n P(AB) P(A)
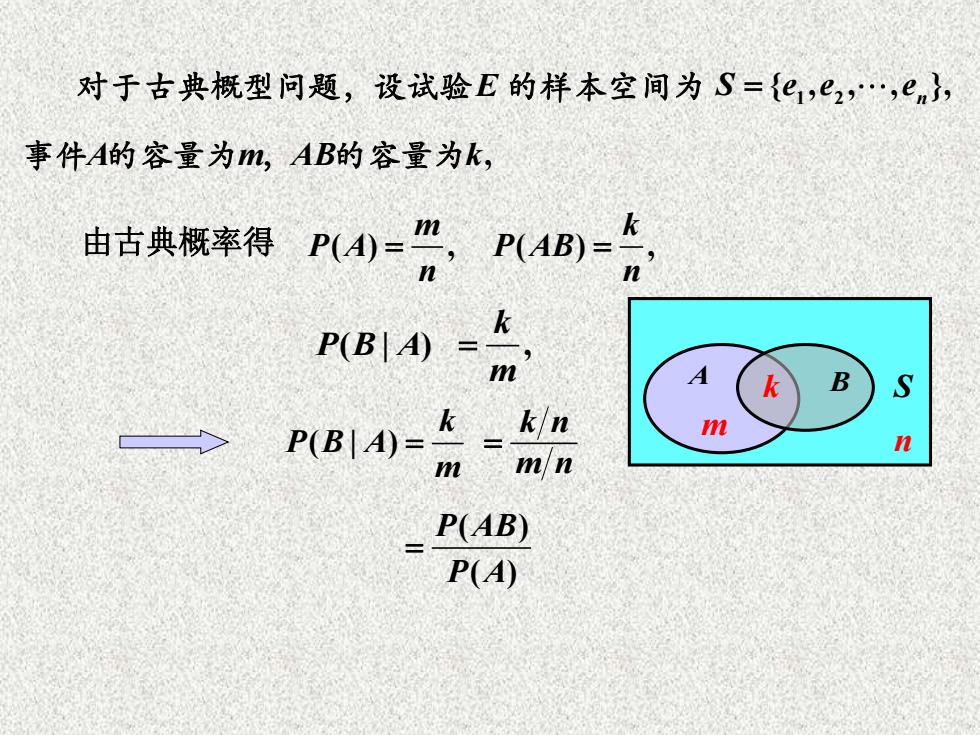
对于古典概型问题,设试验E 的样本空间为 1 2 { , , , }, S e e e = n 事件A m AB k 的容量为 , 的容量为 , A B S ( ) , m P A n = ( ) , k P AB n 由古典概率得 = ( | ) k P B A m = P B A ( | ) , k m = n m k ( ) ( ) P AB P A = k n m n =

2定义 设A,B是两个事件,且P(A)>0,称 P(B)=P(AB) P(A) 为在事件A发生的条件下事件B发生的条件概率 若P(B)>0,同样可称 P(41B)= P(AB) P(B) 为在事件B发生的条件下事件A发生的条件概率
2 0 定义 设 A B P A , , ( ) 0, 是两个事件 且 称 为在事件 A B 发生的条件下事件 发生的条件概率. 若P B( ) 0 ,同样可称 ( ) ( | ) ( ) P AB P A B P B = 为在事件B发生的条件下事件A发生的条件概率. ( ) ( ) ( ) P AB P B A P A =

P(BIA)= P(AB) 30性质 P(A) 条件概率P(~A)符合概率定义中的三个条件(可验证) 1°非负性:P(BA)≥0 2°规范性:P(S|A)=1 3°可列可加性:设B,B2,.是两两互不相容的事件,有 PUB1I=2PB1A 所以,概率具有的性质都适用于条件概率, 如:P(A|B)=1-P(A|B) P(AUA,B)=P(A B)+P(A,B)-P(AA,B)
条件概率P( |A)符合概率定义中的三个条件(可验证) 1° 非 负 性 : P B A ( | ) 0 2°规 范性 : P S A ( | ) 1 = 3°可列可加性 :设 1 2 B B, , 是两两互不相容的事件,有 1 1 ( | ) ( | ) i i i i P B A P B A = = = 3 0 性质 所以,概率具有的性质都适用于条件概率. 1 2 1 2 1 2 P A A P A P A P A A ( ) | | | B B B B = + − ( ( ) ( ) ) | 如:P A P A ( ) ( ) | | B B = −1 . ( ) ( | ) ( ) P AB P B A P A =