
当事件A与B互不相容时,AUB记作A+B: 7.对立(互逆):若A事件与事件B有且仅有一个发生, 即AUB=2且AB=·,则称事件A与事件B为对立事件或互逆事件,其 中事件B叫做事件A的逆事件,记作B=A,事件A叫做事件B的逆事 件,记作A=B 如在E,中,A与B互逆 8.运算规律: 1)AUB=BUA,A∩B=BnA· (2)(AUB)C=ACUBC,(AB)UC=(AUC)(BUC). (3)AUB=AnB,U4=∩4 (4)AnB=AUB,∩4=UA (5)A-B=A-AB=AB
当事件 A 与 B 互不相容时, A B 记作 A+ B . 8.运算规律: (1) A B = B A , A B = B A . (2) (A B)C = AC BC , (AB)C = (AC)(B C) . (3) AB = A B , . = = = 1 k 1 k k Ak A (4) AB = A B , . = = = 1 k 1 k k Ak A (5) A− B = A− AB = AB . 7.对立(互逆):若 事件与事件 有且仅有一个发生, 即 且 ,则 A B 称事件 与事件 为对立事件或互逆事件,其 中事件 叫做事件 的逆事件,记作 ,事件 叫做事件 的逆事 件,记作 . A B = AB = B A B A A B = A B A= B 如在 E2 中, A 与 B 互逆.

例某工人加工三个零件,设4,表示事件 “第i个零件是合格品”式=1,2,3),试用4243表示下列事件: (I)只有第一个零件是合格品: 2)只有一个零件是合格品: (3)至少有一个零件是合格品: (4)最多有一个零件是合格品. 解四个事件分别设为A,B,C,D,则有 (1)A=4424: (2)B=4424U4424,U44249 (3)C=4U4U4(C=AA4月 4)D=A443UB =4424U444U444U4424 或 D=A4 UA4 UA4
“第 个零件是合格品”( =1,2,3),试用 , , 表示下列事 件: 例 某工人加工三个零件,设 Ai 表示事件 i i A1 A2 A3 (1) 只有第一个零件是合格品; (2) 只有一个零件是合格品; (3) 至少有一个零件是合格品; (4) 最多有一个零件是合格品. 解 四个事件分别设为 A , B , C , D ,则有 (1) A = A1 A2 A3 ; (2) B = A1 A2 A3 A1 A2 A3 A1 A2 A3 ; (3) ( ) C = A1 A2 A3 C = A1 A2 A3 ; (4) D = A1 A2 A3 B 或 . = A1 A2 A3 A1 A2 A3 A1 A2 A3 A1 A2 A3 D = A1 A2 A1 A3 A2 A3

第二节概率的古典定义 在一个试验中,有许多随机事件。一个事件在一次试验中可能发生,也 可能不发生.有的事件发生的可能性大,有的事件发生的可能性小。概率就 是用来刻划事件发生的可能性大小的数量指标。 一、概率的统计定义 1.频率 定义1设A为试验E中的一个事件,把试验E在相同条件下重复进行次,如 果事件4发生的次数为”4,则称”4为事件A在n次试验中发生的频率,记为 fn(A),即 h n(4)=”4 设试验B的基本空间为2,A为E中的随机事件,4,42,,4为E中两两 互不相容的事件,则由定义1易知频率具有下述性质: 性质10≤fn(4小≤1. 性质2∫n(2)=1 性质3fn(4U4UU4n)=fn(4)+fn(4)++fn(4m)
在一个试验中,有许多随机事件.一个事件在一次试验中可能发生,也 可能不发生.有的事件发生的可能性大,有的事件发生的可能性小.概率就 是用来刻划事件发生的可能性大小的数量指标. 一、概率的统计定义 设试验 的基本空间为 , 为 中的随机事件, 为 中两两 互不相 E A E A1 , A2 , , Am E 容的事件,则由定义1易知频率具有下述性质: 性质1 0≤ ≤1 f n (A) . 性质2 f n ( ) = 1 . 性质3 f n (A1 A2 Am ) = f n (A1 ) + f n (A2 ) ++ f n (Am ) . 1.频率 定义1 设 A 为试验 E 中的一个事件,把试验 E 在相同条件下重复进行 n 次,如 果事件 发生的次数为 ,则称 为事件 在 次试验中发生的频率,记为 即 A A n n nA A n f (A) n . n n f A A n ( ) = , 第二节 概率的古典定义
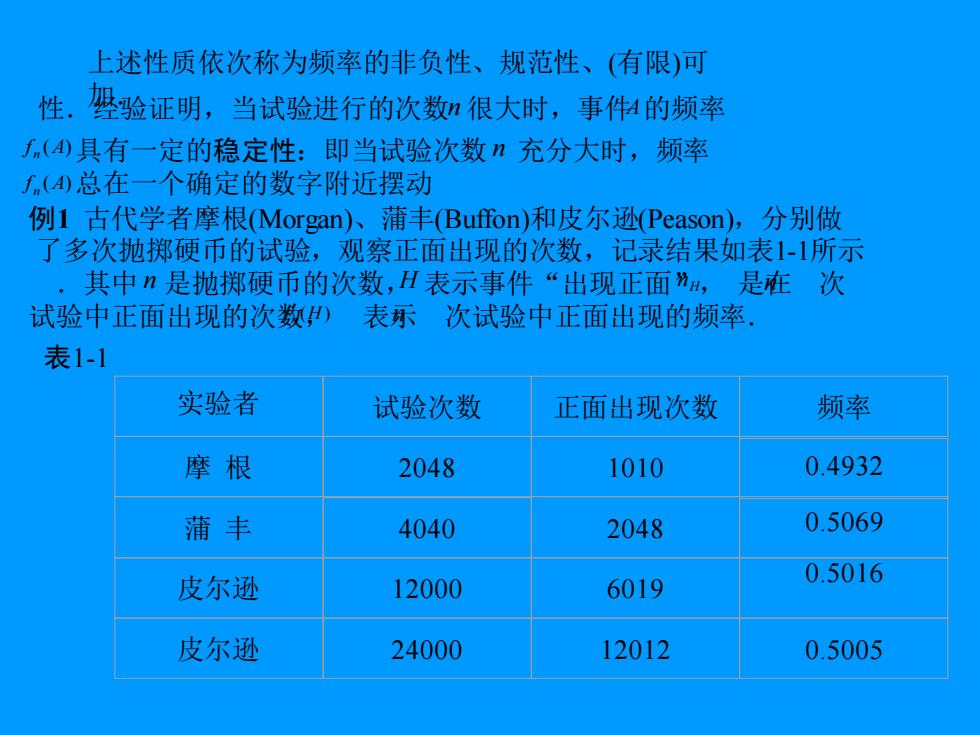
上述性质依次称为频率的非负性、规范性、(有限)可 性。堡验证明,当试验进行的次数很大时,事件利的频率 f(4)具有一定的稳定性:即当试验次数n充分大时,频率 (4)总在一个确定的数字附近摆动 例1古代学者摩根(Morgan)、蒲丰(Buffon)和皮尔逊(Peason),分别做 了多次抛掷硬币的试验,观察正面出现的次数,记录结果如表1-1所示 其中n是抛掷硬币的次数,H表示事件“出现正面”,是在次 试验中正面出现的次数)表乐次试验中正面出现的频率. 表1-1 实验者 试验次数 正面出现次数 频率 摩根 2048 1010 0.4932 蒲丰 4040 2048 0.5069 皮尔逊 0.5016 12000 6019 皮尔逊 24000 12012 0.5005
上述性质依次称为频率的非负性、规范性、(有限)可 性.加.经验证明,当试验进行的次数 n 很大时,事件 A 的频率 具有一定的稳定性:即当试验次数 充分大时,频率 f n (A) 总在一个确定的数字附近摆动 f n (A) n 例1 古代学者摩根(Morgan)、蒲丰(Buffon)和皮尔逊(Peason),分别做 了多次抛掷硬币的试验,观察正面出现的次数,记录结果如表1-1所示 .其中 是抛掷硬币的次数, 表示事件“出现正面”, 是在 次 试验中正面出现的次数, 表示 次试验中正面出现的频率. n H H n f n (H ) n n 表1-1 实验者 试验次数 正面出现次数 频率 摩 根 2048 1010 蒲 丰 2048 0.5069 皮尔逊 12000 6019 皮尔逊 24000 12012 0.5005 4040 0.5016 0.4932

从表1-1可以看到,当试验次数n很大以后,频 率fn()在0.5附近摆动,并逐渐稳定于0.5. 我们把频率,(A)围绕摆动的稳定值P,就叫做事件 A的概率,即有概率的统计定义如下: 2,概率的统计定义 定义2在相同的条件下重复进行n次试验,如果当n增大时, A事件的频率,()=”稳定地在某一常数p附近摆动, 则称常数P为事件A的概率,记P(A)三p 为根据这一定义,可以把由大量重复试验所得到的事件的频率作为事 件概率的近似值. 二、古典概型 1.等可能概型(也叫做古典概型):具有以下特点的试验称为 等可能概型: (①)只有有限个基本事件,即基本空间为有限空间, 2={01,023,0n};
从表1-1可以看到,当试验次数 很大以后,频 率 在0.5附近摆动,并逐渐稳定于0.5. n f (H ) n 我们把频率 围绕摆动的稳定值 ,就叫做事件 的概率,即有概率的统计定义如下: f (A) n p A 2.概率的统计定义 定义2 在相同的条件下重复进行 次试验,如果当 增大时, 事 件 的 频 率 n n A 稳 定 地 在 某 一 常 数 附近摆动, n n f A A n ( ) = p 则称常数 为事件 的概率,记 为 . p A P(A) = p 根据这一定义,可以把由大量重复试验所得到的事件的频率作为事 件概率的近似值. 二、古典概型 1.等可能概型(也叫做古典概型):具有以下特点的试验称为 等可能概型: (i) 只有有限个基本事件,即基本空间为有限空间, = {1 , 2 , , n };