
#农平4?理学院.2002ULTURAI第四章不定积分
第四章 不定积分

第一节不定积分的概念与性质原函数与不定积分的概念不定积分的性质基本积分公式■小结思考题
第一节 不定积分的概念与性质 ◼ 原函数与不定积分的概念 ◼ 不定积分的性质 ◼ 基本积分公式 ◼ 小结 思考题
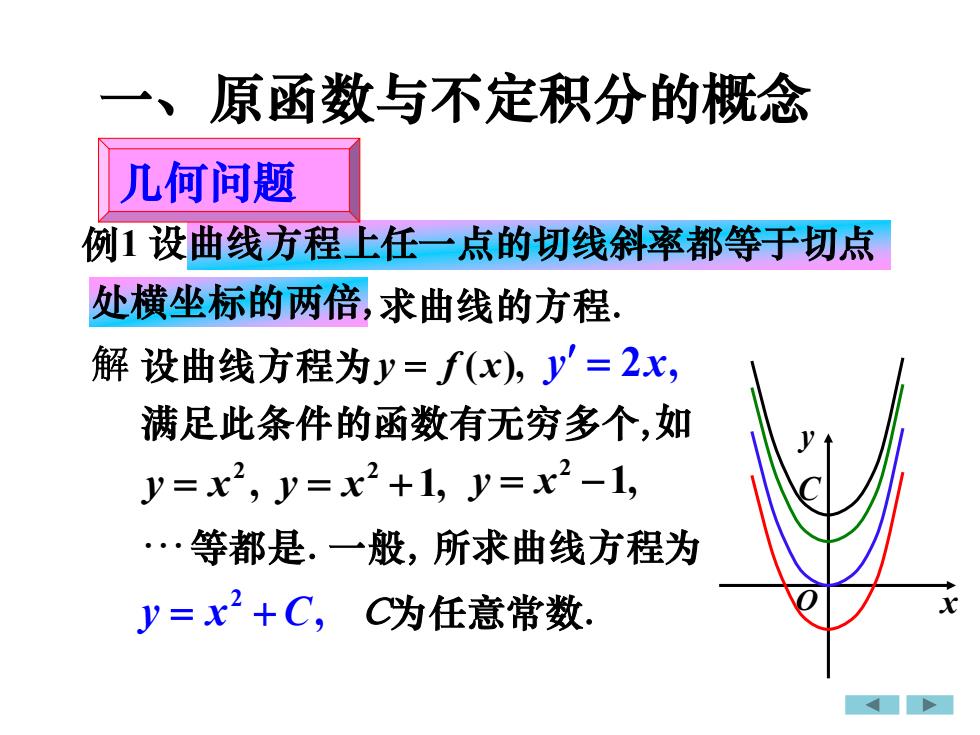
原函数与不定积分的概念一、几何问题例1设曲线方程上任一点的切线斜率都等于切点处横坐标的两倍求曲线的方程解设曲线方程为y=f(x),y=2x,满足此条件的函数有无穷多个,如y=x2, y=x2+1, y=x2-1,·等都是一般,所求曲线方程为x=x2+C,C为任意常数
一、原函数与不定积分的概念 几何问题 解 例1 设曲线方程上任一点的切线斜率都等于切点 处横坐标的两倍,求曲线的方程. 设曲线方程为 y = f (x), y = 2x, 满足此条件的函数有无穷多个,如 , 2 y = x 1, 2 y = x + 1, 2 y = x − 等都是. 一般, 所求曲线方程为 , 2 y = x + C C为任意常数. x y O C

1.原函数定义1或如果在区间I上,F'(x)= f(x)dF(x) = f(x)dx, 则称 F(x)为f(x)在I上的一个原函数如 (sin x)'=cosx 或由dsin x = cos xdx 知F(x)= sin x是f(x)= cos x在(-o0,+oo)上的一个(F(x)c= sinx+C也是 f(x)= cos x原函数的原函数,其中C为任意常数
定义1 如 (sin x) 1. 原函数 F( x) = f ( x) dF(x) = f (x)dx , 如果在区间I上, 则称 F(x)为f (x)在I上的 或 原函数. = cos x 一个 或由 dsin x = cos xdx 知 F(x) = sin x 是 f (x) = cos x在(− ,+ )上的一个 原函数. F(x) + C 也是 f (x) = cos x 的原函数,其中 C 为任意常数. C C = sin x +C

一般,若F(x)为f(x)的一个原函数 则F(x)+C亦为f(x)的原函数(C为任意常数)因[F(x)+C}' =F'(x) =f(x)一个函数如果有原函数,就有无穷多个如果F(x)是f(x)在区间I上的一个定理结论原函数,则f(x)在区间I上的任一原函数都可表为 F(x)+C 的形式,其中C为某一常数定理表明:形如F(x)+C的一整族函数是(x)的全部原函数
一般, 若F(x) F( x) 亦为f (x) 的原函数(C为任意常数). 因 [F(x) + C] = 一个函数如果有原函数,就有无穷多个. 如果F(x)是f (x) 在区间I上的一个 则 f (x) 在区间I上的任一原函数都 F(x) + C 其中C为某一常数. 则 定理 定理表明: F(x) + C 的一整族函数 F(x) = f ( x). 形如 + C 是f(x)的全部原函数. 为f (x)的一个原函数, 原函数, 结 论 可表为 的形式