第五章定积分习题课主要内容典型例题
第五章 定积分 主要内容 典型例题 习 题 课
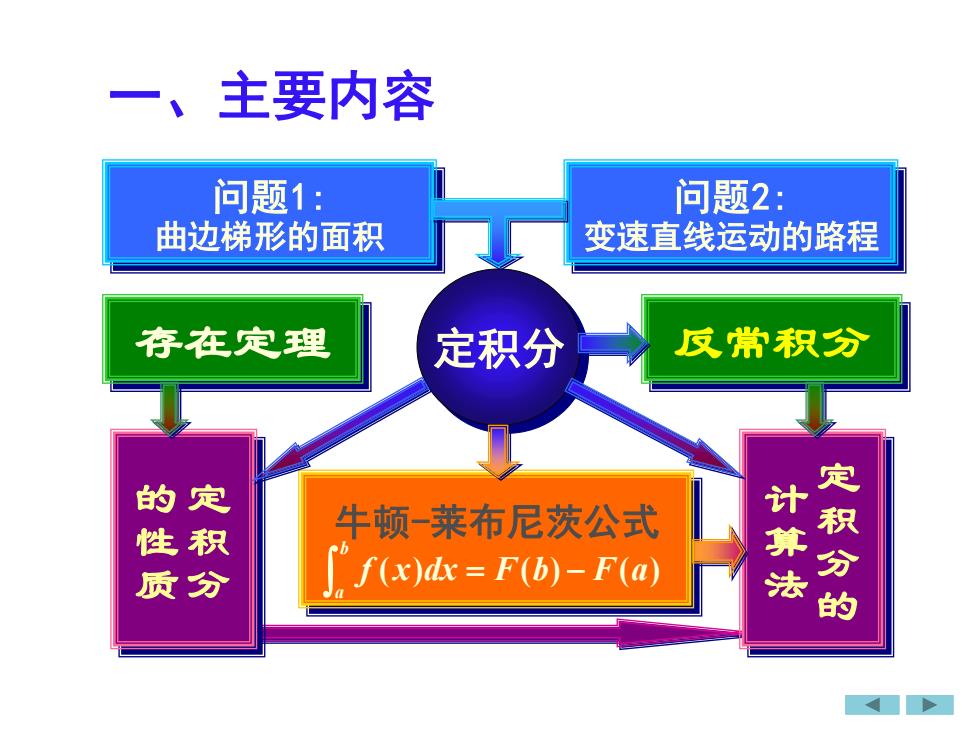
一、主要内容问题1:问题2:曲边梯形的面积变速直线运动的路程存在定理反常积分定积分定积分的的定计算法牛顿-莱布尼茨公式性积f(x)dx = F(b)-F(a)质分
问题1: 曲边梯形的面积 问题2: 变速直线运动的路程 存在定理 定积分 反常积分 定 积 分 的 性 质 定 积 分 的 计 算 法 牛顿-莱布尼茨公式 f ( x)dx F(b) F(a) b a = − 一、主要内容

1、问题的提出实例1(求曲边梯形的面积A)曲边梯形由连续曲线 y=f(x)(f(x)≥O)x轴与两条直线x=a、x=b所围成nEf(5)Ax;A = lim2→0i1
1、问题的提出 实例1 (求曲边梯形的面积A) i n i A = f i x = → lim ( ) 1 0 曲边梯形由连续曲线 y = f ( x)( f (x) 0)、 x轴与两条直线x = a 、x = b所围成

实例2(求变速直线运动的路程)设某物体作直线运动,已知速度v=v(t)是时间间隔[T,T,1上t 的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程SnEv(t,)At;s = lim2>0i=1方法:分割、求和、取极限
实例2 (求变速直线运动的路程) i n i i s = v t = → lim ( ) 1 0 设某物体作直线运动,已知速度v = v(t)是时间 间隔[ , ] T1 T2 上t 的一个连续函数,且v(t) 0, 求 物体在这段时间内所经过的路程 S. 方法:分割、求和、取极限

2、定积分的定义定义 设函数f(x)在[a,b]上有界,在[a,b]中任意若干若干个分点a=x,<x<x,<..<x-<x.=b把区间[a,b]分成n个小区间,[xo,xi],[xi,x,],...[xn-1,xn],各小区间的长度依次为△x,=x;一Xi-1,(i=1,2,)在各小区间上任取一点,(E△x,)
2、定积分的定义 设函数 f (x)在[a,b]上有界,在[a,b]中任意 若干若干个分点 a x x x x x b = 0 1 2 n−1 n = 把区间[a,b]分成n个小区间, 各小区间的长度依次为xi = xi − xi−1,(i = 1,2, ), 在各小区间上任取 一点 i ( i xi), 定义 [ , ],[ , ], [ , ], x0 x1 x1 x2 xn−1 xn