吉林大学：《高等数学》课程电子教案（PPT课件）第四章 多元函数微积分（习题课）

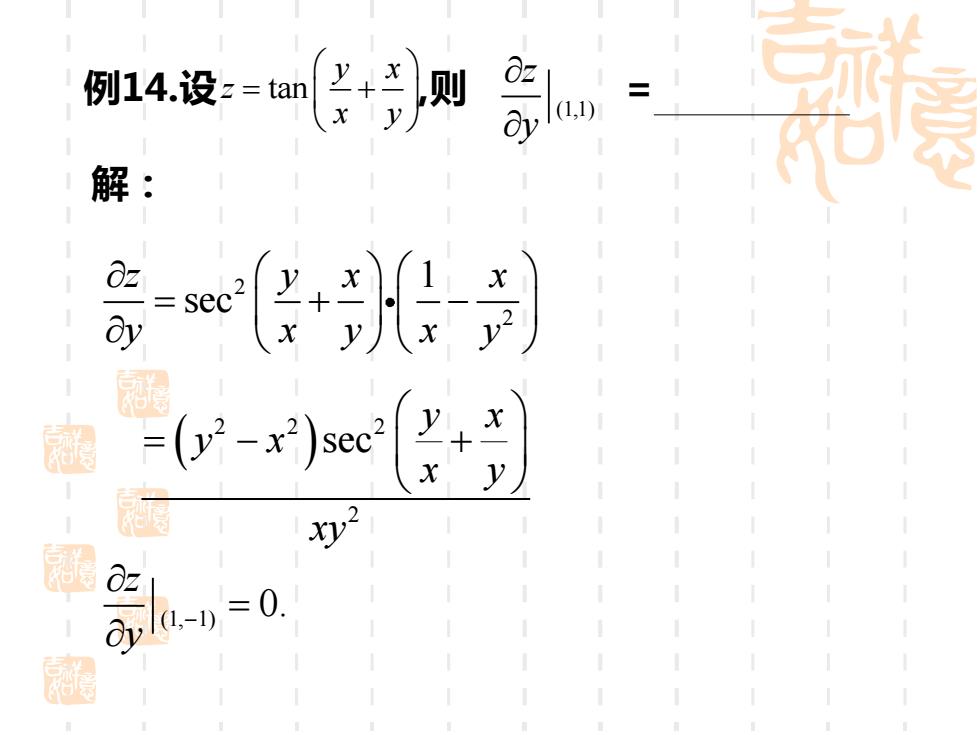
例14.设：=tan 则 解： sec 〔发到 y ≈0 la.-D

tan y x z x y   = +     例14. 设 , 则 (1,1) zy = 解： 2 2 1 sec z y x x y x y x y      = + −          ( ) 2 2 2 2 sec y x y x x y xy   = − +     (1, 1) 0. zy −  = 

例15.设z=x3y+x2y则 解： 3x2y+292=6xy+2

3 5 2 z x y x y = + 2 2zx 例15. 设 , 则 = 解： 2 2 5 5 2 3 2 , 6 2 z z x y xy xy y x x   = + = +  

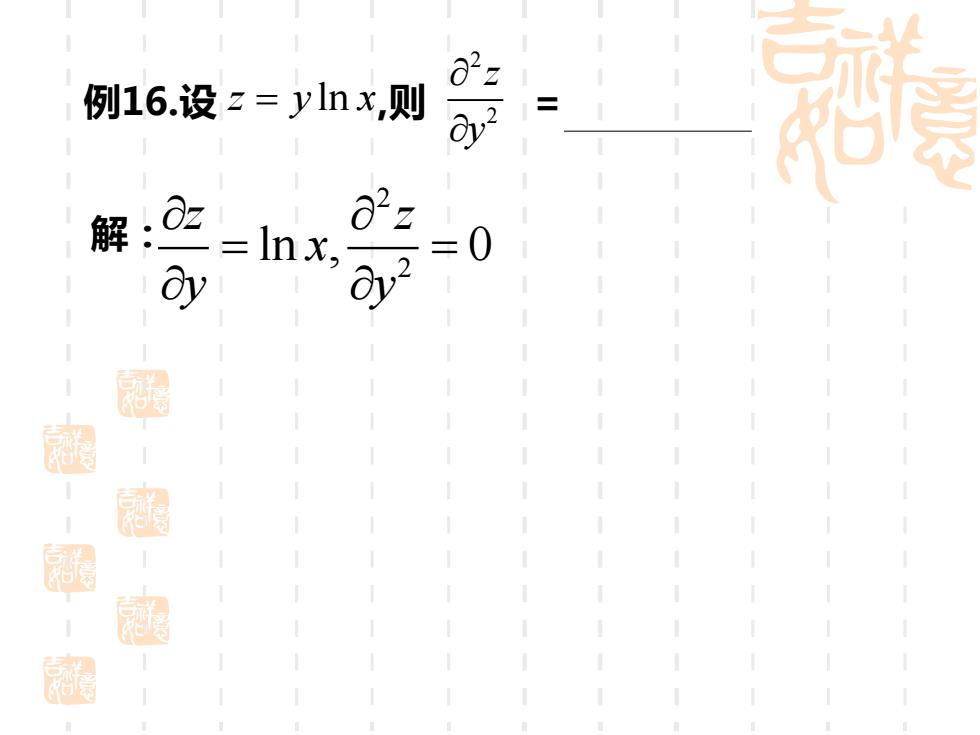
Oz 例16.设z=ylnx,则 -Ix. 解：

例16. 设 z y x = ln , 则 = 2 2zy 解： 2 2 ln , 0 z z x y y   = =  

大学 NIVERSTTY CHIM 1840 高等数兴 第九十六讲 多元品数微积分司题保 主讲教师： 总课时：124

主讲教师：高彦伟 总课时：124 第九十六讲 多元函数微积分习题课

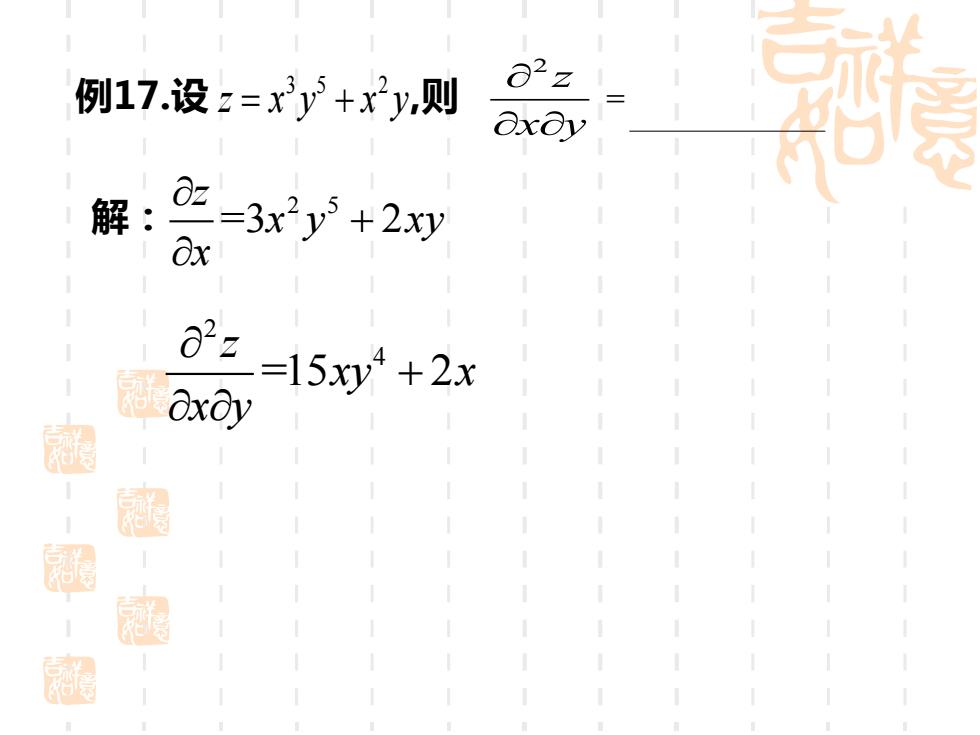
例17.设z=xy3+x2y,则 解：产-3xy+2y Ox 02z=15y2+2x @xdy 赵汉

例17. 设 z x y x y = + 3 5 2 , 则 2 z x y    = 解： 2 5 =3 2 z x y xy x +  2 4 =15 2 z xy x x y  +  