
证明 1).设<A,*>存在两个以上的么元,不妨假设e1, e2是A,*>的两个么元, e1=e1*e2=e2 可知e1=e2,即<A,*>的么元是唯一的。 2025/5/13 计算机与信息工程学院 16
2025/5/13 计算机与信息工程学院 16 证明 1).设<A, * >存在两个以上的幺元,不妨假设e1, e2是<A, * >的两个幺元, e1 =e1 *e2= e2 可知e1=e2,即<A, * >的幺元是唯一的

证明(续) 2).设e是<A,*>的么元,则由么元的定义知:使得对 /x∈A,都有:X*e=e*X=X, 即有:X*e=x与e*X=x, 所以:e既是<A,*>的左么元,又是<A,米>的右么元。 3).若e1、e是<A,*>的左、右么元, e=e1*er=er 可知e1=er,即左、右么元相等; 为此有:x个e=x=x个e1=e1个x,所以:e=e1。 2025/5/13 计算机与信息工程学院 17
2025/5/13 计算机与信息工程学院 17 证明(续) 2).设e是<A, * >的幺元,则由幺元的定义知:使得对 xA,都有:x * e=e * x=x, 即有:x * e=x与e * x=x, 所以:e既是<A, * >的左幺元,又是<A, * >的右幺元。 3).若el、er是<A, * >的左、右幺元, el=el * er =er 可知el=er,即左、右幺元相等; 为此有:x∧er =x=x∧el=el∧x,所以:e=el

定理设“*”是集合A上的二元运算。 1)若<A,*>存在零元,则该零元唯一; 2)若<A,*>存在零元,则该零元一定是左、右 零元; 3)若<A,*>存在左、右零元,则该左、右零元 一定相等,且是零元。 2025/5/13 计算机与信息工程学院 18
2025/5/13 计算机与信息工程学院 18 定理 设“*”是集合A上的二元运算。 1)若<A, * >存在零元,则该零元唯一; 2)若<A, * >存在零元,则该零元一定是左、右 零元; 3)若<A, * >存在左、右零元,则该左、右零元 一定相等,且是零元
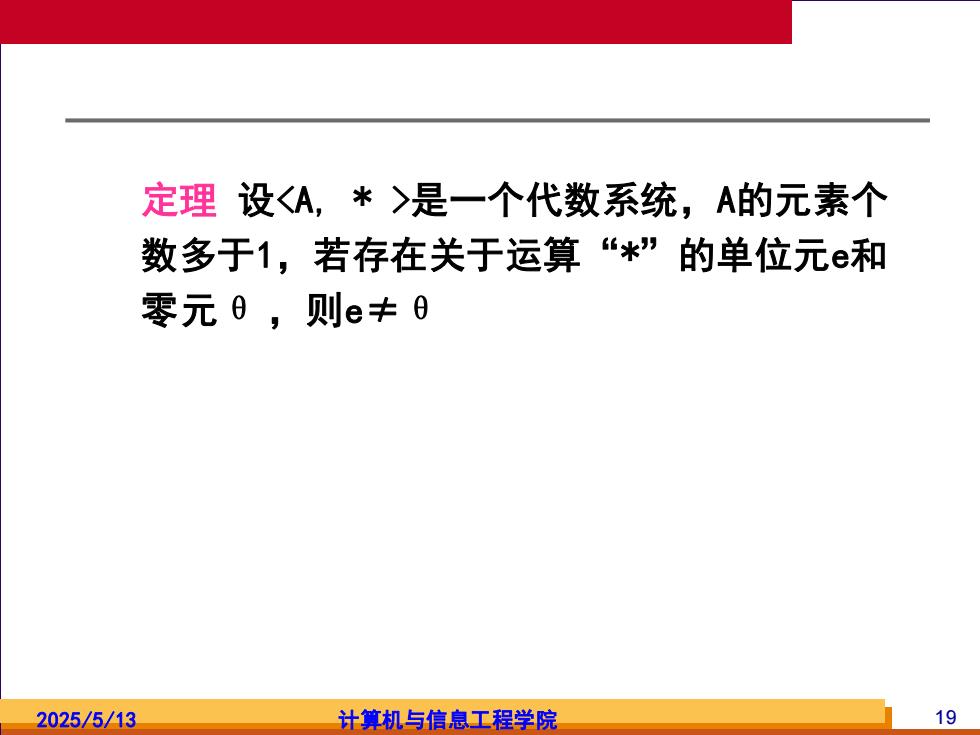
定理设<A,*>是一个代数系统,A的元素个 数多于1,若存在关于运算“*”的单位元e和 零元0,则e卡日 2025/5/13 计算机与信息工程学院 19
2025/5/13 计算机与信息工程学院 19 定理 设<A, * >是一个代数系统,A的元素个 数多于1,若存在关于运算“*”的单位元e和 零元θ ,则e≠θ

逆元性质 定理设“*”是集合A上的二元运算,〈A,米> 是一个代数系统,若“*”满足结合建且e是 <A,>的么元(即么元存在),则对VaeA, l)若a存在逆元,则该逆元唯一; 2)若a存在逆元,则该逆元一定是该元素的左、 右逆元; 3)若a存在左、右逆元,则该左、右逆元一定相 等,且是该元的逆元。 2025/5/13 计算机与信息工程学院 20
2025/5/13 计算机与信息工程学院 20 逆元性质 定理 设“*”是集合A上的二元运算,<A, * > 是一个代数系统,若“*”满足结合律且e是 <A,*>的幺元(即幺元存在),则对aA, 1)若a存在逆元,则该逆元唯一; 2)若a存在逆元,则该逆元一定是该元素的左、 右逆元; 3)若a存在左、右逆元,则该左、右逆元一定相 等,且是该元的逆元