《离散数学》课程教学资源（试卷习题）试卷（答案）19

离散数学考试题（十九）参考答案 一、填空20%（每空2分） 3 1、02、P→-Q:3、(PA)A(PA(0VS):4 5、自反性、对称性、传递性：6、UR'=R: 7、①运算*在A上封闭，②*在A上可结合，③*在A上存在么元，④A中每个元素都有逆元： 8、Va,b∈A,f(a+b)=f(a)⊕f(b),f(a·b)-f(a)⑧f(b) 9、v-e+r=2:10、e=v-1。 二、选择题10%（每小题2分） 1、A:2、C:3、D:4、B:5、D 三、解： 符号化：前提x(F(x)→G(x)AH(x),3x(F(x)AR(x) 结论3x(F(x)AR(x)AG(x》 推理演绎：(1)3x(F(x)AR(x》 (2)F(c)R(c) ES(1) (3)x(F(x)→G(x)AH(x》 P (4(F(c)→G(c)AH(c》 US(3) (⑤)F(d) TO) (6)G(c)H(c) T5)(41 (7)R(c) TO)I (8)Gc) T(61 (9)F(c)R(c)G(c) T5)7)(81 (10)3(F(x)AR(x)AG(x) EG(9) 四、解： 名

离散数学考试题（十九）参考答案 126 一、填空 20%（每空 2 分） 1、 0；2、 P → Q ；3、(P  Q)  (P  (Q  S)) ；4、 5、自反性、对称性、传递性；6、 +  = R = R i i  1 ； 7、①运算*在 A 上封闭，②*在 A 上可结合，③*在 A 上存在幺元，④A 中每个元素都有逆元； 8、a,b  A , f (a + b) = f (a)  f (b) , f (a b) = f (a)  f (b) 9、 v −e + r = 2 ； 10、e = v −1 。 二、选择题 10%（每小题 2 分） 1、A； 2、C； 3、D； 4、B； 5、D。 三、解： 符号化：前提 x(F(x) → G(x)  H(x)) , x(F(x)  R(x)) 结论 x(F(x)  R(x)  G(x)) 推理演绎：（1） x(F(x)  R(x)) P （2） F(c)  R(c) ES(1) (3) x(F(x) → G(x)  H(x)) P (4) (F(c) → G(c)  H(c)) US(3) (5) F(c) T(2)I (6) G(c)  H(c) T(5)(4)I (7) R(c) T(2)I (8) G(c) T(6)I (9) F(c)  R(c)  G(c) T(5)(7)(8)I (10) x(F(x)  R(x)  G(x)) EG(9) 四、解：

离散数学考试题（十九）参考答案 w4n4n4n-p<s}= a4u4u4u.-00<xs}-0<xs 五、解： (1)关系图为 0-2 xy+2-0与xy-2-0两直线将实平面划分 -2)-.(00)X2,0) 为三个区域xy+2>0,xy-2<0为包含 原点的狭长区域。 (0,-2 (2) ①R自反 任意实数x,Xx+2>0,Xx-2<0,所以直线yx上的点在区域内，即x,xER,故R 自反： ②R对称 若<x,y>ER有 8238. y-x+2=-(x-y-2)>0 所以R对称： ③因R自反且结点集非空，故R非反自反： ④因R对称且结点集非空，并非全是孤立点，故R不是反对称： ⑤由-y+3>0得-2≤y<+2所以<4>eR雨<1，-1tR 所以R4不是传递的。 六、解： 不是布尔代数。因s的最个元为1，最大元为24但2-兰-2,122r2≠24 vb且GCD2,2)=GCD2,24)=2≠1。 七、解： 用Kruskal算法，选一条权最小的边，逐一选取剩余的边中与已知边未构成回路且权数最小 127

离散数学考试题（十九）参考答案 127 （1）    = =           =   1 1 2 3 1 0 n n A A A x x （2）      = =            =   1 1 2 3 0 1 1 0 n x x n A A A x x 五、解： （1）关系图为 x-y+2=0 与 x-y-2=0 两直线将实平面划分 为三个区域 x-y+2>0 ， x-y-2<0 为包含 原点的狭长区域。 （2） ①R 自反 任意实数 x，x-x+2>0 ， x-x-2<0 , 所以直线 y=x 上的点在区域内，即 <x , x>  R , 故 R 自反； ②R 对称 若  x, y  R 有    − −  − +  2 0 2 0 x y x y 得    − − = − − +  − + = − − −  2 ( 2) 0 2 ( 2) 0 y x x y y x x y 即  y, x  R 所以 R 对称； ③因 R 自反且结点集非空，故 R 非反自反； ④因 R 对称且结点集非空，并非全是孤立点，故 R 不是反对称； ⑤由    − −  − +  2 0 2 0 x y x y 得 x − 2  y  x + 2 所以   R 4 1 1, 而  1,−1  R 所以 R4 不是传递的。 六、解： 不是布尔代数。因 S24 的最小元为 1，最大元为 24，但 12 2 24 2 = = ，LCM(2,12)=12  24， vb 且 GCD(2,2) = GCD(2,24) = 2  1 。 七、解： 用 Kruskal 算法，选一条权最小的边，逐一选取剩余的边中与已知边未构成回路且权数最小 （0，2） （2，0） （0，-2） （-2，0） （0，0）

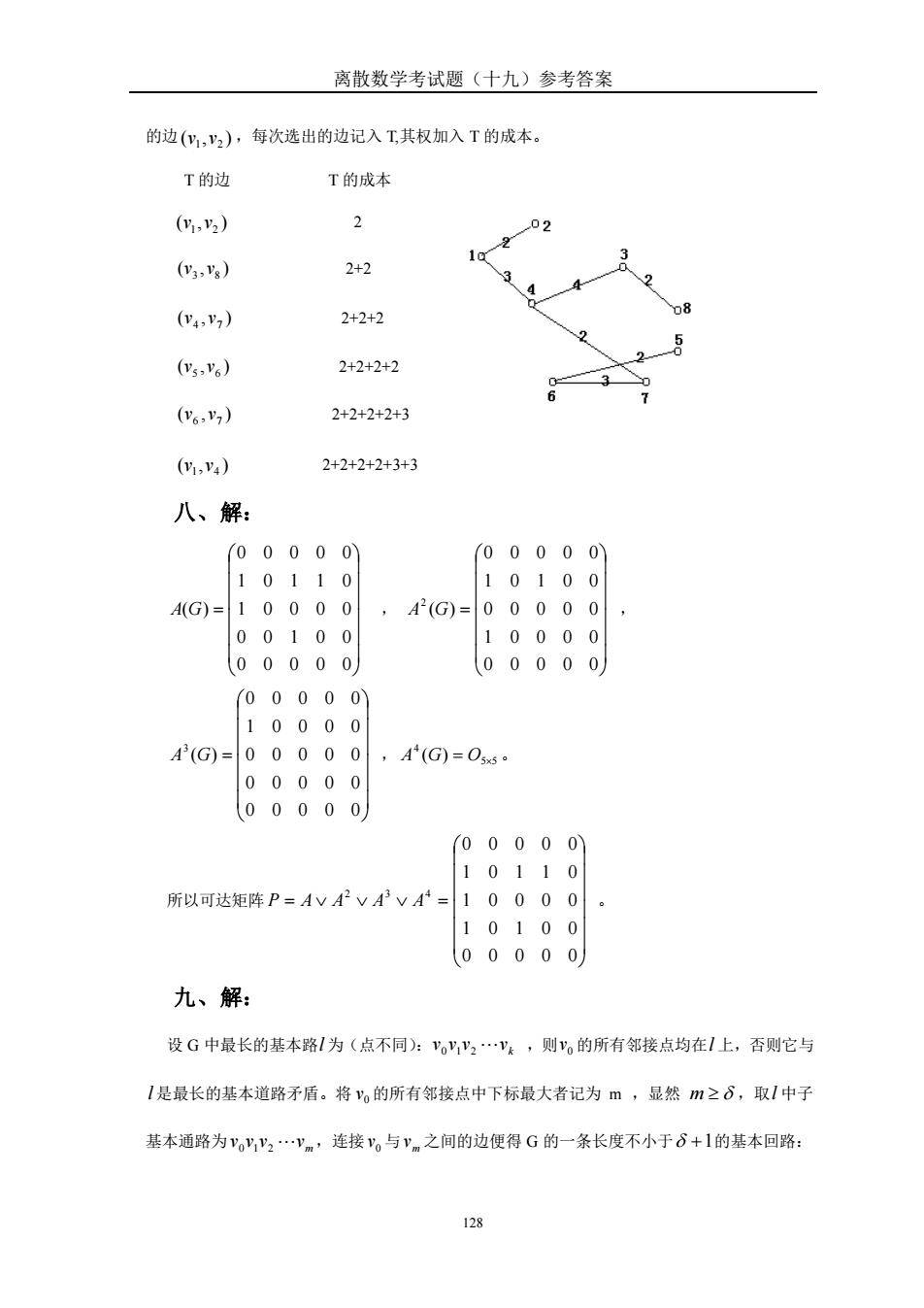
离散数学考试题（十九）参考答案 的边(，)，每次选出的边记入工其权加入T的成本 T的边 T的成本 (g,2) 02 (,g) 2+2 (v4,) 2+2+2 2 (y,) 2+2+2+2 3 (v6,) 2+2+2+2+3 (m,4) 2+2+2+2+3+3 八、解： (00000 (00000) 10110 10100 A(G)=10000 A2(G)=00000 00100 10000 00000 00000 (00000\ 10000 A(G)=00000,A(G=05. 00000 (00000 (00000 10110 所以可达矩阵P=AVAVAVA=10000。 10100 00000 九、解： 设G中最长的基本路I为（点不同）：，y2v,则。的所有邻接点均在1上，否则它与 1是最长的基本道路矛盾。将。的所有邻接点中下标最大者记为m,显然m≥δ，取1中子 基本通路为yy2.vm,连接。与v之间的边便得G的一条长度不小于6+1的基本回路：

离散数学考试题（十九）参考答案 128 的边 ( , ) 1 2 v v ，每次选出的边记入 T,其权加入 T 的成本。 T 的边 T 的成本 ( , ) 1 2 v v 2 ( , ) 3 8 v v 2+2 ( , ) 4 7 v v 2+2+2 ( , ) 5 6 v v 2+2+2+2 ( , ) 6 7 v v 2+2+2+2+3 ( , ) 1 4 v v 2+2+2+2+3+3 八、解：                 = 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 0 0 A(G) ，                 = 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 ( ) 2 A G ，                 = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 ( ) 3 A G ， 5 5 4 ( ) A G = O  。 所以可达矩阵                 =    = 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 0 0 2 3 4 P A A A A 。 九、解： 设 G 中最长的基本路 l 为（点不同）： k v v v v 0 1 2 ，则 0 v 的所有邻接点均在 l 上，否则它与 l 是最长的基本道路矛盾。将 0 v 的所有邻接点中下标最大者记为 m ，显然 m   ，取 l 中子 基本通路为 m v v v v 0 1 2 ，连接 0 v 与 m v 之间的边便得 G 的一条长度不小于  +1 的基本回路：

离散数学考试题（十九）参考答案 0

离散数学考试题（十九）参考答案 129 0 1 2 1 Q v v v v v =  m