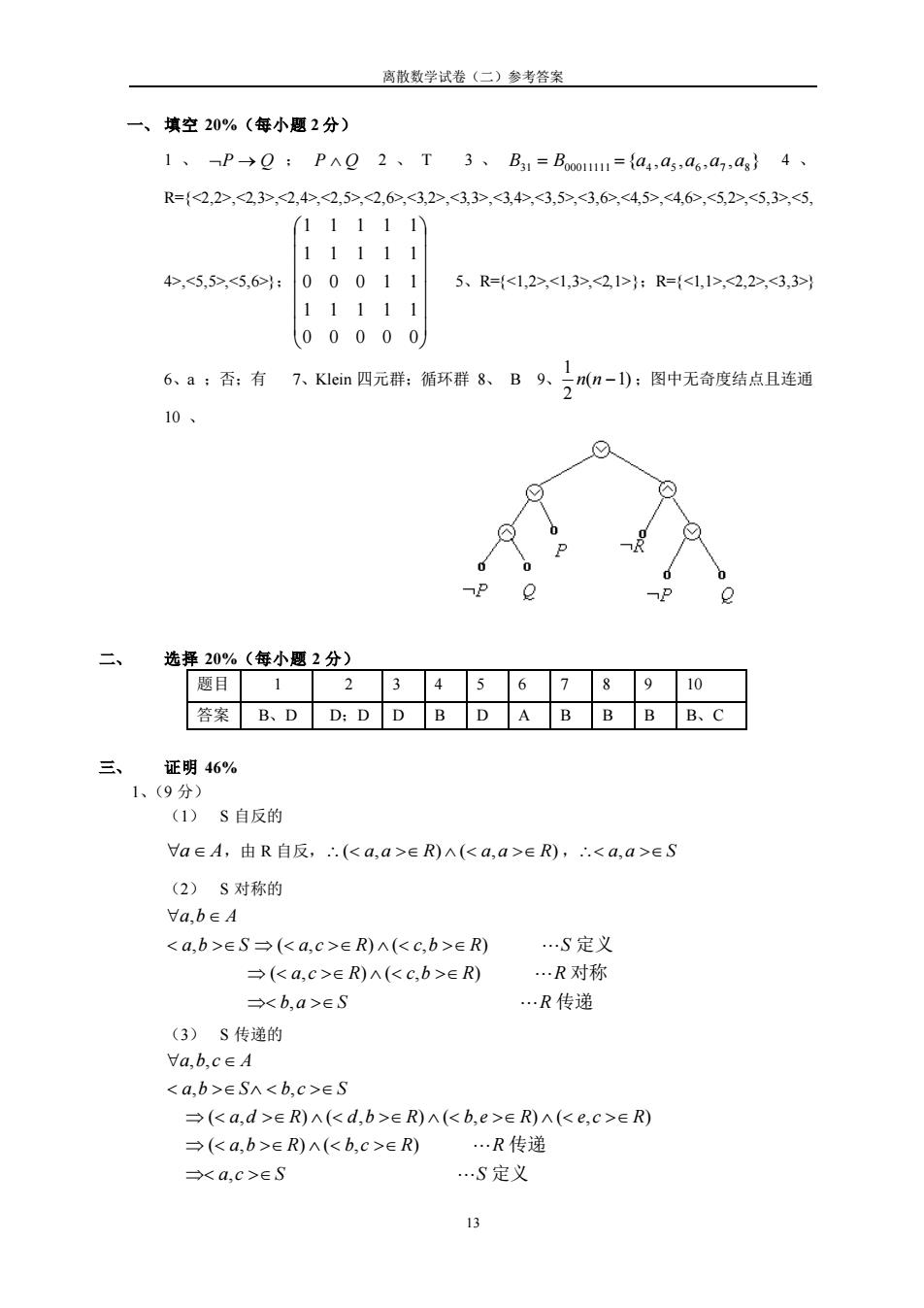
离散数学试卷(二)参考答案 一、填空20%(每小题2分) 1、P→:PA2、T3、B1=B0={a4,a5,a6,a,a}4 R={2,2>,<2,3>,<2,4>,<2,5>,<2,6,<32>,<33,<34,<3,5>,<3,6,<45>,<46,<52>,<5,3,<5, 11111 11111 4>,<5,5>,<5,6⊙ 00011 5、R=<1,2>,<1,3>,<21>:R=<1,1>,<2,2>,<3,3 11111 00000 6、a:否香:有7、Klein四元群:循环群8、B9、亏n-):图中无奇度结点且连通 10、 选择20%(每小思2分) 题目12345678910 答案B、DD:D DBDABBBB、C 三、证明46% 1、(9分) (1)S自反的 a∈A,由R自反,∴(ka,a>eR)A(ka,a>eR),∴<a,a>eS (2)S对称的 Va,beA <a,b>ES(<a,c>ER)A(<c,b>ER) ,S定义 (<a.c>ER)A(<c,b>ER) .R对称 <baES .R传递 (3)S传递的 ta,b,c∈A <a,b>ESA<b,c>ES (<a,d>ER)n(<d,b>ER)A(<b,e>ER)A(<e,c>ER) →(<a.b>ER)A(<b.c>∈R) .R传递 <a,c>ES .S定义
离散数学试卷(二)参考答案 13 一、 填空 20%(每小题 2 分) 1 、 P → Q ; P Q 2 、 T 3 、 { , , , , } B31 = B00011111 = a4 a5 a6 a7 a8 4 、 R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5, 4>,<5,5>,<5,6>}; 0 0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 5、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>} 6、a ;否;有 7、Klein 四元群;循环群 8、 B 9、 ( 1) 2 1 n n − ;图中无奇度结点且连通 10 、 二、 选择 20%(每小题 2 分) 题目 1 2 3 4 5 6 7 8 9 10 答案 B、D D;D D B D A B B B B、C 三、 证明 46% 1、(9 分) (1) S 自反的 a A ,由 R 自反, ( a,a R) ( a,a R) , a,a S (2) S 对称的 传递 对称 定义 b a S R a c R c b R R a b S a c R c b R S a b A , ( , ) ( , ) , ( , ) ( , ) , (3) S 传递的 定义 传递 a c S S a b R b c R R a d R d b R b e R e c R a b S b c S a b c A , ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) , , ,

离散数学试卷(二)参考答案 由(1)、(2、(3)得:S是等价关系。 2、11分 证明:设P(x):x是个舞蹈者:Qx):x很有风度:Sx):x是个学生:a:王华 上述句子符号化为: 前提:x(P(x)→Q(x)、S(a)AP(a)结论:3x(S(x)AQx》-3分 ①S(a)AP(a) ②x(P(x)→Q(x)》 ③Pa)→Qa) US② ④P(a) TOI ⑤Q(a) T③④I ⑥s(a) TOI ⑦S(a)nga) T⑤⑥1 ⑧3x(S(x)AQx) EG⑦ .11分 3、10分 证明:h,b2eB,(亿≠b)∫满射3a,a∈A 使f(a)=b,f(a2)=b2,且f(a)≠fa2),由于f提函数,∴.a1≠a2 又g(b)={x|(x∈A)A(f(x)=b)h,g(b)={x|(x∈A)A(f(x)=b2)} a∈g6ba∈gb)但a¥g(bba2Eg(b,)∴g(b)≠g(b) 由b,b,任意性知,g为单射。 4、8分 证明:设G中两奇数度结点分别为u和v,若山,v不连通,则G至少有两个连通分支 G、G,使得u和v分别属于G和G2,于是G1和G2中各含有1个奇数度结点,这与图论 基本定理矛盾,因而山,V一定连通。 5、8分 证明:证G中任何两结点之和不小于n 反证法:若存在两结点u,v不相邻且d()+d(v)≤n-1,令={仙,以,则G-V1是具 有n-2个结点的简单图,它的边数m≥(n-1n-2)+2-(m-),可得 m≥2n-2n-3)+1,这与G=G-V为m2个结点为简单图的题设矛盾,因而G中任何 14
离散数学试卷(二)参考答案 14 由(1)、(2)、(3)得;S 是等价关系。 2、11 分 证明:设 P(x):x 是个舞蹈者; Q(x) :x 很有风度; S(x):x 是个学生; a:王华 上述句子符号化为: 前提: x(P(x) → Q(x))、 S(a) P(a) 结论: x(S(x) Q(x)) .3 分 ① S(a) P(a) P ② x(P(x) → Q(x)) P ③ P(a) → Q(a) US② ④ P(a) T①I ⑤ Q(a). T③④I ⑥ S(a) T①I ⑦ S(a) Q(a) T⑤⑥I ⑧ x(S(x) Q(x) EG⑦ .11 分 3、10 分 证明 : , ,( ) b1 b2 B b1 b2 f 满射 a1 ,a2 A 1 1 2 2 1 2 1 2 使f (a ) = b , f (a ) = b , 且 f (a ) f (a ),由于f是函数, a a ( ), ( ) ( ), ( ) ( ) ( ) ( ) { | ( ) ( ( ) )}, ( ) { | ( ) ( ( ) )} 1 1 2 2 1 2 2 1 1 2 1 1 2 2 a g b a g b a g b a g b g b g b g b x x A f x b g b x x A f x b = = = = 但 又 由b1 ,b2任意性知 , g为单射。 4、8 分 证明:设 G 中两奇数度结点分别为 u 和 v,若 u,v 不连通,则 G 至少有两个连通分支 G1、G2 ,使得 u 和 v 分别属于 G1和 G2,于是 G1 和 G2 中各含有 1 个奇数度结点,这与图论 基本定理矛盾,因而 u,v 一定连通。 5、8 分 证明: 证 G 中任何两结点之和不小于 n。 反证法:若存在两结点 u,v 不相邻且 d(u) + d(v) n −1,令 { , } 1 V = u v ,则 G-V1 是具 有 n-2 个结点的简单图,它的边数 ( 1)( 2) 2 ( 1) 2 ' 1 m n − n − + − n − , 可 得 ( 2)( 3) 1 2 ' 1 m n − n − + ,这与 G1=G-V1 为 n-2 个结点为简单图的题设矛盾,因而 G 中任何
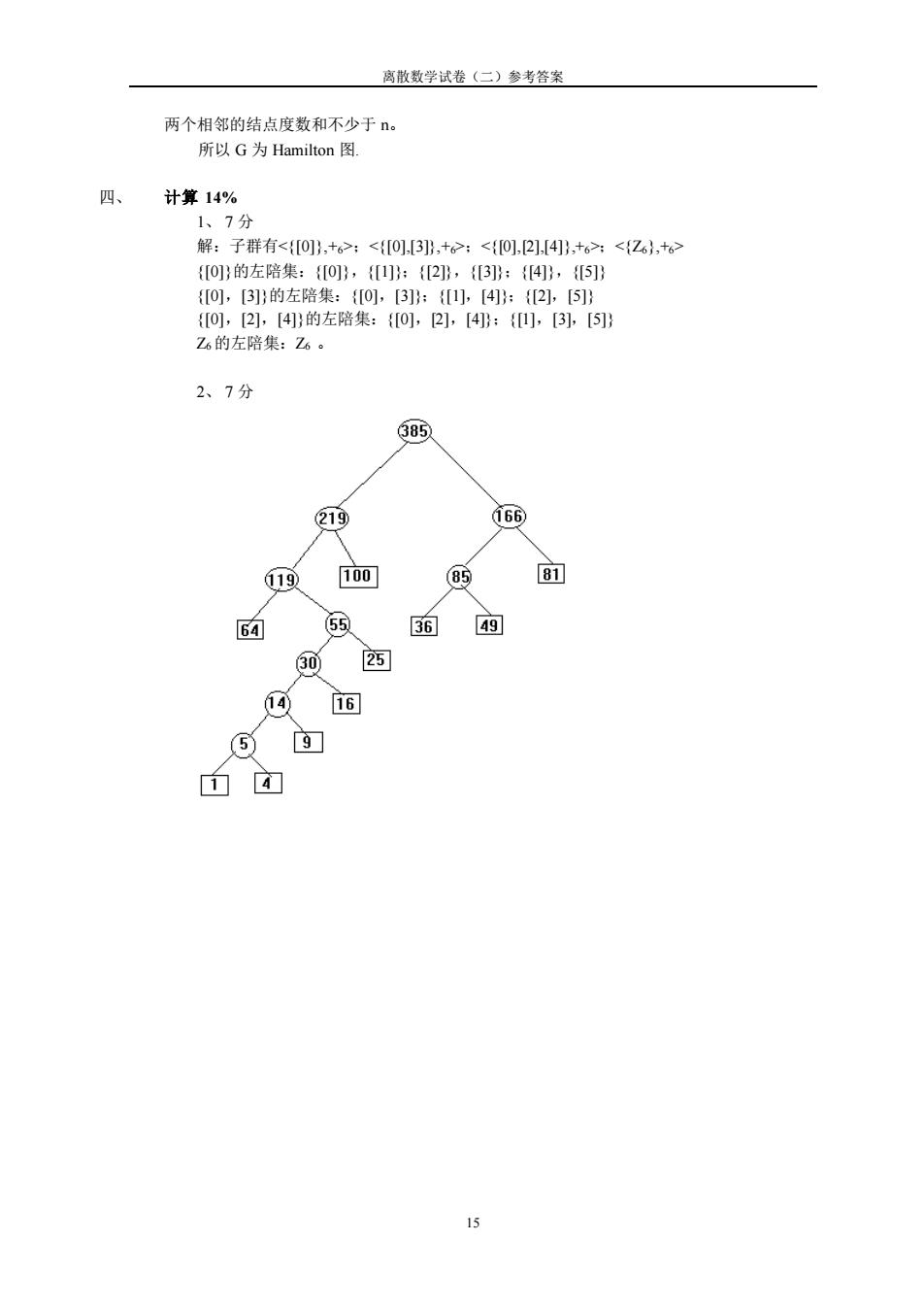
离散数学试卷(二)参考答案 两个相邻的结点度数和不少于n。 所以G为Hamilton图. 四、 计算14% 1、7分 解:子群有<{[0],+6>;<{[0,[3]},+。⊙;<{[0],2],[4],+6>:<{Z6},+6> {[0]}的左陪集:{[0]},{1]}:{[2]},{[3]}:{[4},5} {[0,[3]}的左陪集:{[0],[3]:{[1],[4}:{[2],[5]} {[0,[2],[4]}的左陪集:{[0],2],[4}:{[1,[3],[5} Z6的左陪集:Z6。 2、7分 385 219 166 119 100 85 81 64 55 36 49 30 25 1④ 16 5 9 4
离散数学试卷(二)参考答案 15 两个相邻的结点度数和不少于 n。 所以 G 为 Hamilton 图. 四、 计算 14% 1、 7 分 解:子群有<{[0]},+6>;<{[0],[3]},+6>;<{[0],[2],[4]},+6>;<{Z6},+6> {[0]}的左陪集:{[0]},{[1]};{[2]},{[3]};{[4]},{[5]} {[0],[3]}的左陪集:{[0],[3]};{[1],[4]};{[2],[5]} {[0],[2],[4]}的左陪集:{[0],[2],[4]};{[1],[3],[5]} Z6 的左陪集:Z6 。 2、 7 分