《离散数学》课程教学资源（试卷习题）试卷（答案）16

离散数学试卷（十六）参考答案 一、填空20%（每小题2分） 1 题目 (1)(2)(3)(4)(5) 答案Y NN N N 二、8% (3x(P(x)v(Oy》→(y)Ry) 台(3xPx)v(Qy》v(y)Ry) (-(x)P(x)-(VyX(Q(y)v(Vy)R(y) ((Vx)-P(x)(Q(y))v(Vy)R(y) ((Vx)-P(x)(y-Q(y))v(V=)R(=) 台(x)3y:(-P(x)A-Qy》vR(e) 前束析取范式 台(x3y:(-P(x)vR(=)A(-Qy)vR(E》 前束合取范式 三、8% (01000 00110 关系矩阵：M=00000 00001 (00000 关系图 a b d 传递闭包：(R)=UR'=-UR

离散数学试卷（十六）参考答案 104 一、填空 20%（每小题 2 分） 题目 1 2 3 4 5 6 （1） （2） （3） （4） （5） 答案 Y N N N Y Y N Y N Y 二、8% 前束合取范式 前束析取范式 ( )( )( )(( ( ) ( )) ( ( ) ( )) ( )( )( )(( ( ) ( )) ( )) (( ) ( ) ( ( )) ( ) ( ) (( ) ( ) ( ( )) ( ) ( ) ( ( ) ( ) ( )( ( )) ( ) ( ) (( ( ) ( ( )) ( ) ( ) (( )( ( ) ( ( )) ( ) ( ) x y z P x R z Q y R z x y z P x Q y R z x P x y Q y z R z x P x y Q y y R y x P x y Q y y R y x P x yQ y y R y x P x yQ y y R y                                                    →  三、8% 关系矩阵：                 = 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 M R 关系图： 传递闭包：   5 1 1 ( ) =  = = = i i i i t R R R

离散数学试卷（十六）参考答案 (01000(01000)00110 0011000110 00001 Me=MeMR=0000000000=00000 0000100001 00000 (00000(00000 (00000 (00110)01000)(00001） 0000100110 00000 M=MeMR=0000000000=00000 0000000001 00000 00000(00000(00000 (00001)01000)(00000) 000000011 0 00000 Me=MpoMR=0000000000-00000=M 0000000001 00000 0000000000 (00000 (01111) 00111 M+M+M+M+M=000 00 00001 00000 t(R)-(<a,b>.<ac,<ad>,<a.e>,<b,c>,<b,d>,<b,e>,<d,e>j. 四、10% 证明：对<G,>中任意元素a和b a3*b3=(a*b)3,.a*(a3*b3)*b-1=a1*(a*b)3*b,即a2*b2=(a*b)2 同理：由a*b4=(a*b)可得a3*b3=(b*a)3 由a3*b5=(a*b)3可得a*b=(b*a) 因此(a3*b3)*(b*a)=(b*a)=a*b即b4*a=a*b 同样可得(a2*b2)*(b*a)=(b*a)3=a3*b3即b3*a=a*b (a*b)*b3=a*b=b+a=b*(b3+a)=b*(a*b)=(b*a)*b 故a*b=b*a 所以<G,>是阿贝尔群 105

离散数学试卷（十六）参考答案 105                 =                                 = = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 2   M R M R M R                 =                                 = = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 3 2   M R M R M R 4 3 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 M R M R M R M R =                 =                                 =  =                   + + + + = 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 1 2 3 4 5 M R M R M R M R M R t (R)={< a , b > , < a, c> , < a, d> , < a ,e > , < b , c > , < b , d > , < b , e > , < d , e > }。 四、10% 证明：对<G,*>中任意元素 a 和 b a b b a a b b a b b a b b a b a b b a b a b b a b a a b b a a b a b b a b a a b b a a b a b a b a b b a a b a b a b b a a b a b a a b b a a b b a b a b * * ( * ) * * * *( * ) *( * ) ( * ) * ( * ) *( * ) ( * ) * * * ( * ) *( * ) ( * ) * * * * ( * ) * ( * ) : * ( * ) * ( * ) * ( * ) , *( * ) * *( * ) * * ( * ) 3 4 4 3 3 3 2 2 3 3 3 3 3 3 3 4 4 4 4 4 5 5 5 4 4 4 4 4 4 3 3 3 3 3 3 1 3 3 1 1 3 1 2 2 2 = = = = = = = = = = = = = = = = =  = = − − − − 故 由于 同样可得 即 因此 即 由 可得 同理 由 可得  ，即 所以<G,*>是阿贝尔群

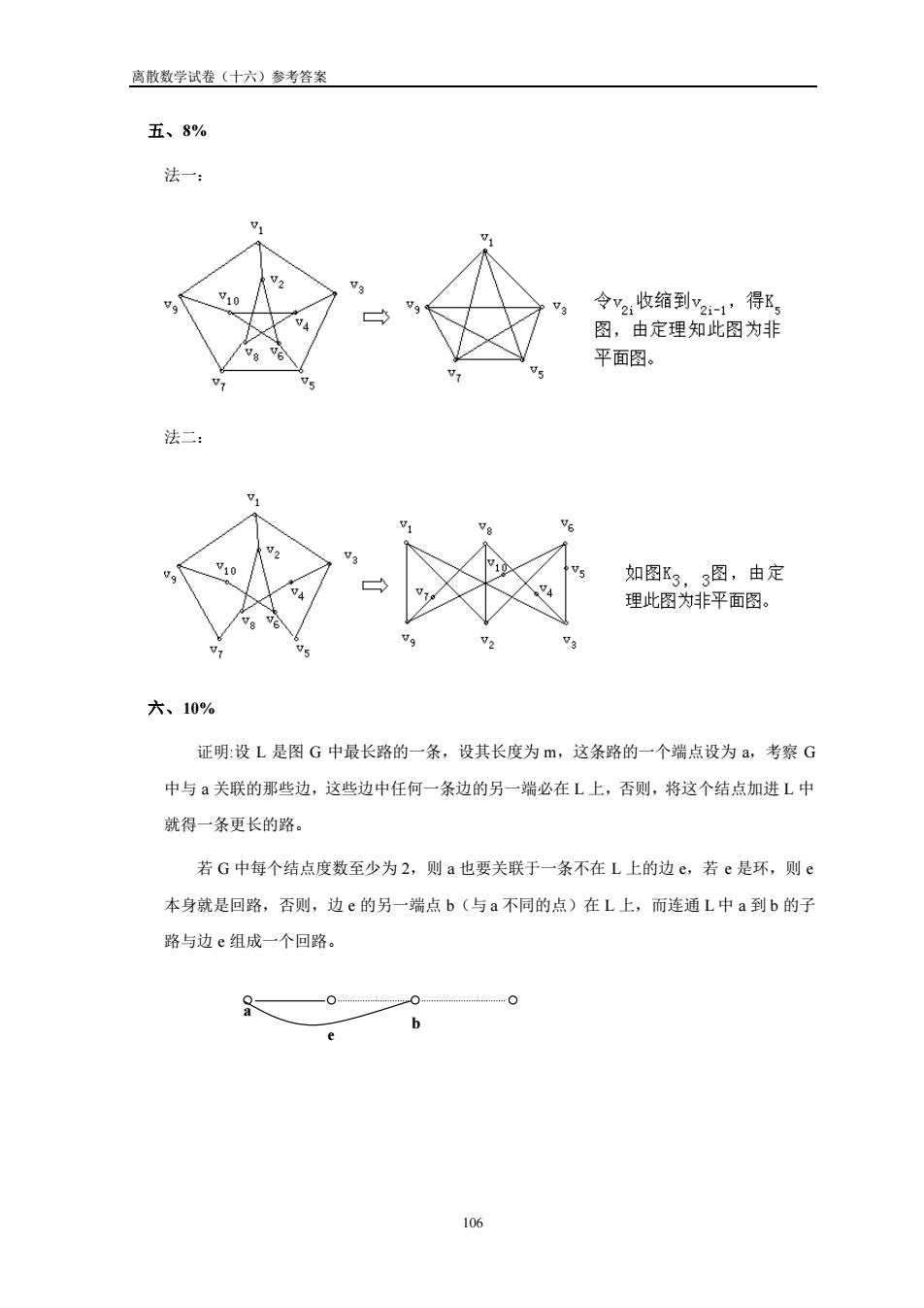
离散数学试卷（十六）参考答案 五、8% 法一： 收缩到v2s 得 图，由定理知此图为非 平面图。 如图K3,3图，由定 理此图为非平面图。 六、10% 证明：设L是图G中最长路的一条，设其长度为m,这条路的一个端点设为a,考察G 中与a关联的那些边，这些边中任何一条边的另一端必在L上，否则，将这个结点加进L中 就得一条更长的路。 若G中每个结点度数至少为2，则a也要关联于一条不在L上的边e,若e是环，则e 本身就是回路，否则，边e的另一端点b(与a不同的点)在L上，而连通L中a到b的子 路与边e组成一个回路。 -0. h

离散数学试卷（十六）参考答案 106 五、8% 法一： 法二： 六、10% 证明:设 L 是图 G 中最长路的一条，设其长度为 m，这条路的一个端点设为 a，考察 G 中与 a 关联的那些边，这些边中任何一条边的另一端必在 L 上，否则，将这个结点加进 L 中 就得一条更长的路。 若 G 中每个结点度数至少为 2，则 a 也要关联于一条不在 L 上的边 e，若 e 是环，则 e 本身就是回路，否则，边 e 的另一端点 b（与 a 不同的点）在 L 上，而连通 L 中 a 到 b 的子 路与边 e 组成一个回路。 a b e

离散数学试卷（十六）参考答案 七、12%（每小题6分） 1、 ①P ②-RVP P ③-R T①②1 ④(SAQ)→R P ⑤R→-(SA) T④E ⑥-(SΛQ) T③⑤I ⑦-SvQ T⑥E ⑧S P(附加前提) ⑨-Q T⑦⑧I ⑩s→Q 2 ①(Gx)P(x) P(附加前提 ②P(e) ESD ③(xXP(x)→O(x)》 ④Pe)→Qe US3 ⑤Q(e) T②④L ⑥(3x)2(x) EG⑤ ⑦(Ex)P(x)→(3x)Q(x) CP o

离散数学试卷（十六）参考答案 107 七、12%（每小题 6 分） 1、 ① P P ② R  P P ③ R T①②I ④ (S  Q) → R P ⑤ R → (S  R) T④E ⑥ (S  Q) T③⑤I ⑦ S  Q T⑥E ⑧ S P(附加前提) ⑨ Q T⑦⑧I ⑩ S → Q CP 2、 ① (x)P(x) P（附加前提） ② P(e) ES① ③ (x)(P(x) → Q(x)) P ④ P(e) → Q(e) US③ ⑤ Q(e) T②④I ⑥ (x)Q(x) EG⑤ ⑦ (x)P(x) → (x)Q(x) CP

离散数学试卷（十六）参考答案 八、12% )(Gx)P(x)→(x(P(x)VQ(x)→R(x)》P (②(Ex)Px) P 3)(x(P(x)vQ(x)→R(x ④P(e) ES② ((Ex)0(x) P ⑥Qd) ES(5) ((P(d)vQd)→R(d US( (Q(d)P(d) T6I (9R(d) T7X81 P(e)R(d) T(4X9)I aD(EyP(e)ARy》 EGQ0 m(Gx(3y(P(x)AR(y》 EGOD 九、12% (1)自反性：(x)eX,由于x+y=x+,故<(xy),(x,)>ER (2)对称性：(x,片，(x2,2)∈X,当<(x,片)，(x2,2)>∈R时 即+乃2=x2+片亦x+片=x+有<（化2乃），(：，片)>∈R (3)传递性：(x,(x2),()∈X, 当<(x,y,x2,乃2)>eR<(x2,2),(x,)>eR时 108

离散数学试卷（十六）参考答案 108 八、12% ⑴ (x)P(x) → (x)((P(x)  Q(x)) → R(x)) P ⑵ (x)P(x) P ⑶ (x)((P(x)  Q(x)) → R(x)) T⑴⑵I ⑷ P(e) ES⑵ ⑸ (x)Q(x) P ⑹ Q(d) ES⑸ ⑺ (P(d)  Q(d)) → R(d) US⑶ ⑻ Q(d)  P(d) T⑹I ⑼ R(d) T⑺⑻I ⑽ P(e)  R(d) T⑷⑼I ⑾ (y)(P(e)  R( y)) EG⑽ ⑿ (x)(y)(P(x)  R( y)) EG⑾ 九、12% （1）自反性： (x, y) X,由于x + y = x + y,故 (x, y),(x, y) R (2) 对称性： (x1 , y1 ),(x2 , y2 ) X,当 (x1 , y1 ),(x2 , y2 ) R时 即x1 + y2 = x2 + y1 亦 x2 + y1 = x1 + y2有 (x2 , y2 ),(x1 , y1 ) R （3）传递性： ( , ),( , ),( , ) ,  x1 y1 x2 y2 x3 y3  X 当 (x1 , y1 ),(x2 , y2 )  R, (x2 , y2 ),(x3 , y3 )  R时