离散数学试卷(二十一)参考答案 一、解 愿号 2 3 4 5 答案 二、解: 结合律 交换律 么元(含左 0(右么 右么元) 0 元) 零元(含左 0 石无) 三、解: (0010 (1101) 1021 0011 A= =2101 1101 1021 3212 1000 0010 1101 (3212 4=4313 3153 由到长度为4的有向路径的条数为3条。 1021 四、解: 两有向图点集的同构映射为 f:→2,2→,→4,→y,→v5 所以两有向图是同构的。 五、解: 设该树有t片树叶,总结点数为∑d(w)=2×2+3×3+4×4+1=29+1 总边数为e=v-1=2+3+4+1-1=8+1 所以,29+=2-(8+0)即13。该树有13片树叶。 六、解: 139
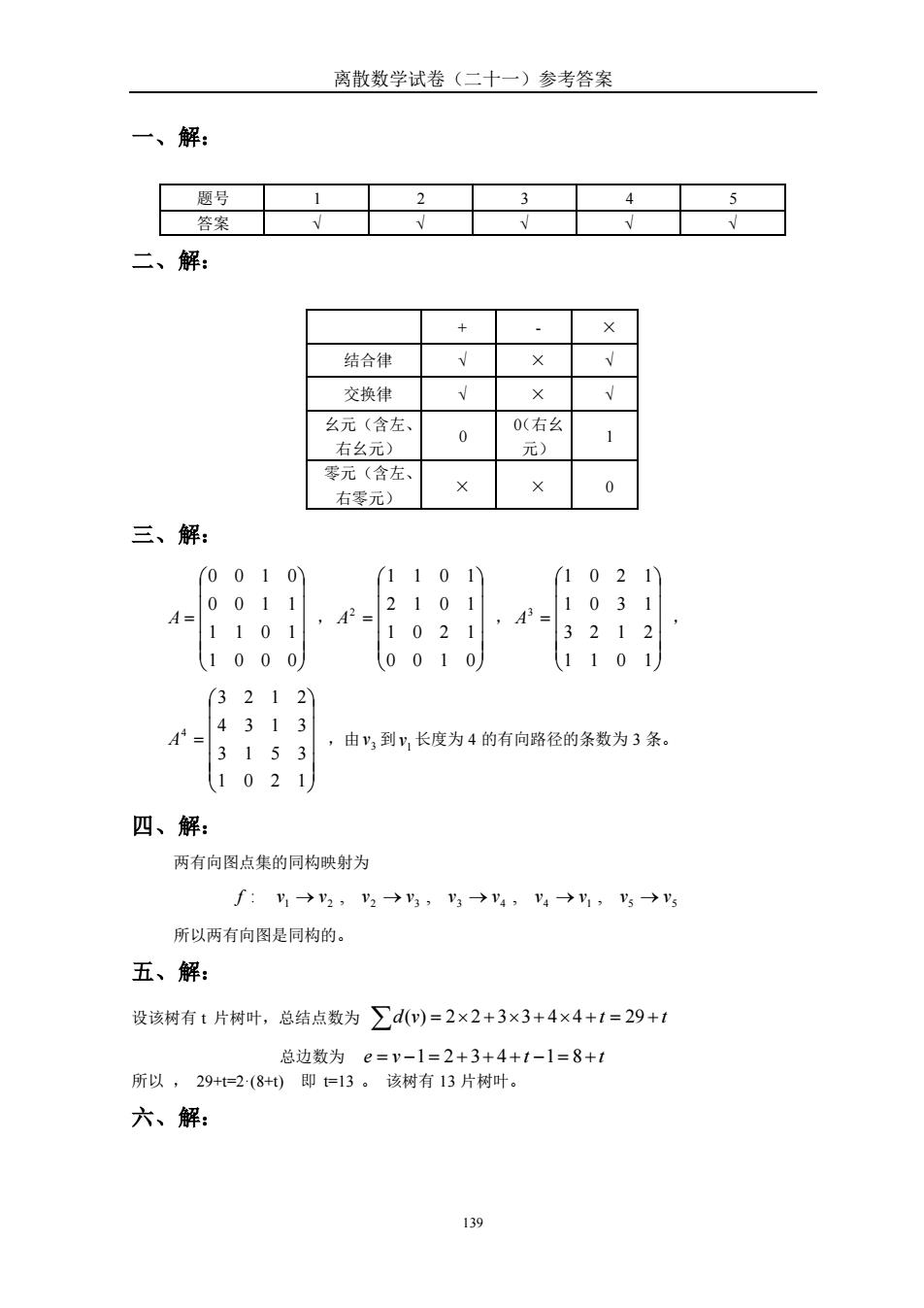
离散数学试卷(二十一)参考答案 139 一、解: 题号 1 2 3 4 5 答案 √ √ √ √ √ 二、解: + - × 结合律 √ × √ 交换律 √ × √ 幺元(含左、 右幺元) 0 0(右幺 元) 1 零元(含左、 右零元) × × 0 三、解: = 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 A , = 0 0 1 0 1 0 2 1 2 1 0 1 1 1 0 1 2 A , = 1 1 0 1 3 2 1 2 1 0 3 1 1 0 2 1 3 A , = 1 0 2 1 3 1 5 3 4 3 1 3 3 2 1 2 4 A ,由 3 v 到 1 v 长度为 4 的有向路径的条数为 3 条。 四、解: 两有向图点集的同构映射为 f : 1 2 2 3 3 4 4 1 5 5 v → v , v → v , v → v , v → v , v → v 所以两有向图是同构的。 五、解: 设该树有 t 片树叶,总结点数为 d(v) = 22 + 33+ 44 + t = 29 + t 总边数为 e = v −1= 2+3+ 4+t −1= 8+t 所以 , 29+t=2·(8+t) 即 t=13 。 该树有 13 片树叶。 六、解:

离散数学试卷(二十一)参考答案 2 七、解: ①g是<R,+>上的同态映射 m,=(a1+b2),m2=(a2+b2√2)∈R gm1+m)=g(a+bV2+a2+b2V2)=g(a,+a2)+(6,+b2)W2)=(a+a2)-(+b2)V2 =(a,-bV2)+(a2-b22)=g(m,)+g(m2) ②g是<R,+>上的满射 m=(a+bN2)∈R,3m'=a-bN2∈R使 g(m)=g(a-b2)=a-(-b)2=a+b2=m所以g是<R,+>上的满射. ③g是<R,+>上的单射 m=(a,+bV2),m2=(a,+bV2)eR,且m,≠m2 则g(m,)=a,-bV2,g(m,)=a-bV2,如果g(m)=g(m) 则(a-a2)-(6-b2)W2=0,∴.必有a,=a2,6=b2这与m≠m2矛盾。 故g(m)≠g(m)。由①,②,③知g是从<R,+>到<R,+>的自同构映射。 八、解: ①G有一个3阶子群 因为在G中除©外,G中元素的阶不可能都为2,否则G是交换群[事实上: x∈G,x2=e,∴x1=x,a*b=(a*b)=b*a=b*a,所以任取两个非么元元素 a,b,则{c,a,b,ab;是G的一个子群,其阶数为4,而4不能整除6,得出矛盾。 于是,g∈G,使g≠e且g*g≠e,从而g的周期为3或6。若g的周期为3,则 (g)是3阶子群。若g的周期为6,则(g)的阶数为3,即得证G有一个3阶子群。 ②G只有一个3阶子群 若G有两个三阶子群H和H,则HOH'是H和H得子群,那么HH的阶只可能为 1和 (i)若H⌒H的阶为3,则H=H: (i)若HnH的阶为1,即HOH'={e 10
离散数学试卷(二十一)参考答案 140 七、解: ① g 是<R ,+ >上的同态映射 ( 2) m1 = a1 + b1 , m2 = (a2 + b2 2) R ( 2) ( 2) ( ) ( ) ( ) ( 2 2) (( ) ( ) 2) ( ) ( ) 2 1 1 2 2 1 2 1 2 1 1 2 2 1 2 1 2 1 2 1 2 a b a b g m g m g m m g a b a b g a a b b a a b b = − + − = + + = + + + = + + + = + − + ② g 是<R ,+ >上的满射 m = (a + b 2) R ,m = a −b 2 R 使 g(m ) = g(a − b 2) = a − (−b) 2 = a + b 2 = m 所以 g 是<R ,+ >上的满射。 ③ g 是<R ,+ >上的单射 ( 2) m1 = a1 + b1 , m2 = (a2 + b2 2) R ,且 m1 m2 则 g(m1 ) = a1 − b1 2 , g(m2 ) = a2 − b2 2 , 如果 ( ) ( ) g m1 = g m2 则 1 2 1 2 1 2 1 2 (a − a ) − (b − b ) 2 = 0 , 必有a = a , b = b 这与 m1 m2 矛盾。 故 ( ) ( ) g m1 g m2 。 由①,②,③知 g 是从<R ,+ >到<R ,+ >的自同构映射。 八、解: ① G 有一个 3 阶子群 因为 在 G 中除 e 外,G 中元素的阶不可能都为 2,否则 G 是交换群[事实上: x G x = e x = x a b = a b = b a = b a 2 −1 −1 −1 −1 , , , ( ) ] ,所以任取两个非幺元元素 a , b,则 {e , a , b , ab}是 G 的一个子群,其阶数为 4,而 4 不能整除 6,得出矛盾。 于是, g G ,使 g e 且 g g e ,从而 g 的周期为 3 或 6。若 g 的周期为 3,则 (g)是 3 阶子群。若 g 的周期为 6,则(g2 )的阶数为 3,即得证 G 有一个 3 阶子群。 ② G 只有一个 3 阶子群 若 G 有两个三阶子群 H 和 H/ ,则 H H 是 H 和 H/ 得子群,那么 H H 的阶只可能为 1 和 3。 (i)若 H H 的阶为 3,则 H = H/ ; (ii)若 H H 的阶为 1,即 H H ={e}

离散数学试卷(二十一)参考答案 :.H,H1=HnH H HT =HH1=3×3=9≥6=lG 这里HH'-{ab|aeH且beH=UaH'sG得出矛盾.。 ac 由①,②知命题成立
离散数学试卷(二十一)参考答案 141 H H G H H H H H H = = = = = 3 3 9 6 这里 H H ab a H b H aH G a H = = { 且 } 得出矛盾。 由①,②知命题成立