
一、填空20%(每小题2分) 1、{0,1,2,3,4,6:2、(B⊕C)-A:3、1:4、(-PVSVR)A(Pv-SvR) 5、1:6、{<1,1>,<1,3>,2,2>,2,4:7、{a.b>,<a,心,<a,d,<b,d,<c,dUh:8、 9、a:a,b,c,d:a,d,c,d:10、c 二、选择20%(每小题2分) 愿目 12 34567890 答案CDB、CC A D C A D BA 三、证明26% 1、证: “→”a,b,ceX若<a,b>,<a,c>eR由R对称性知<b,a>,<c,a>∈R 由R传递性得<b,c>∈R “-”若<a,b>eR,<a,c>∈R有<b,c>eR任意a,beX,因<a,a>∈R 若<a,b>∈R<b,a>∈R所以R是对称的 若<a,b>∈R,<b,c>∈R则<b,a>eRA<b,c>eR∴<a,c>eR即R 是传递的。 2、证a,beC,有f(a)=g(a,fb)=gb),又fb)=-f(b),g(b)=g'(b) ∴fb-)=-(b)=g(b)=gb-) fa★b-)-f(a)*f-(b)-g(a)*g(b-)-g(a★b-) .a★b-eC <C,★>是<G1,★>的子群。 3、证: 6
60105dfca3d04de78d0fae2fb259d7ed.doc 6 一、填空 20% (每小题 2 分) 1、{0,1,2,3,4,6}; 2、(B C) − A ;3、1; 4、(P S R) (P S R) ; 5、1;6、{<1,1>, <1,3>, <2,2>, <2,4> };7、{<a.b>,<a,c>,<a,d>,<b,d>,<c,d>} IA ;8、 9、a ;a , b , c ,d ;a , d , c , d ;10、c; 二、选择 20% (每小题 2 分) 题目 1 2 3 4 5 6 7 8 9 10 答案 C D B、C C A D C A D B A 三、证明 26% 1、 证: “” a,b,c X 若 < a,b >,< a,c > R 由 R 对称性知 < b,a >,< c,a R , 由 R 传递性得 < b, c >R “ ” 若 < a, b > R ,< a, c > R 有 < b, c >R 任意 a,b X ,因 < a, a > R 若 < a, b > R < b,a > R 所以 R 是对称的。 若 < a, b > R , < b, c > R 则 < b,a > R b,c R < a,c > R 即 R 是传递的。 2、 证 a,b C ,有 f (a) = g(a), f (b) = g(b) ,又 ( ) ( ), ( ) ( ) 1 1 1 1 f b f b g b g b − − − − = = ( ) ( ) ( ) ( ) −1 −1 −1 −1 f b = f b = g b = g b f (a ★ b ) f (a)* f (b) g(a)* g(b ) g(a 1 1 1 = = = − − − ★ ) −1 b a ★ b C −1 < C , ★> 是 < G1 , ★>的子群。 3、 证:
①设G有r个面,则2e=立d)2k,即r≤2。面v-e+r=2故 2=-e+r5-e+华即得e52.(8分 k-2 3微得南国为=5=1v=0,送:5不之 所以彼得森图非平面图。(3分) 二、逻辑推演16% 1、证明: ①A P(附加前提)》 ②AVB TOI ③AVB→CAD p ④CAD T②③】 ⑤D T④I ©DVE T⑤I ⑦DVE→F ⑧F T⑥⑦1 ⑨A→F CP 2、证明 ①rPx) P(附加前提) ②P(c) US① ③x(P(x)→Qx》p ④P(c)→Q(c) US③
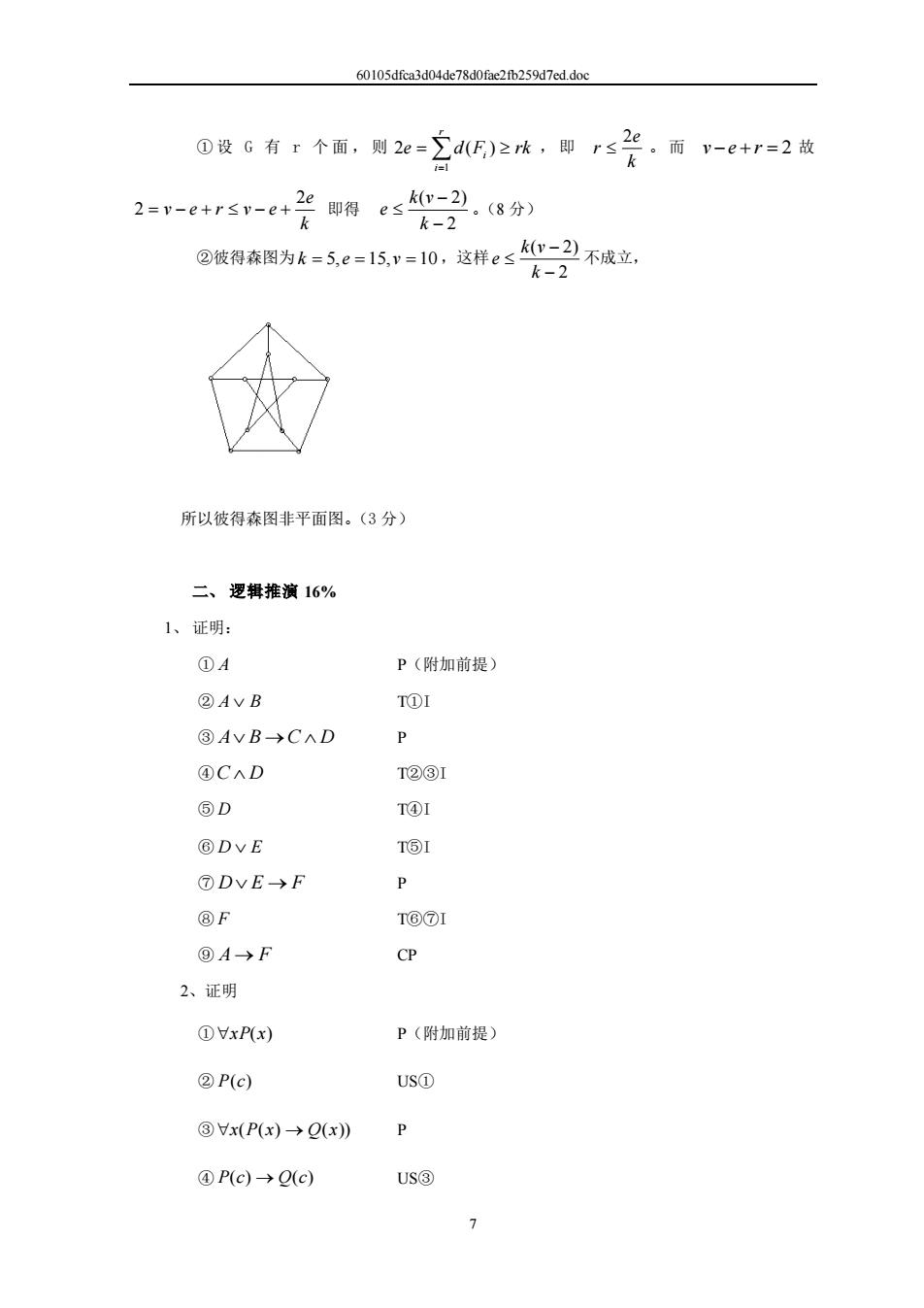
60105dfca3d04de78d0fae2fb259d7ed.doc 7 ① 设 G 有 r 个面,则 e d F rk r i = i =1 2 ( ) , 即 k e r 2 。 而 v −e + r = 2 故 k e v e r v e 2 2 = − + − + 即得 2 ( 2) − − k k v e 。(8 分) ②彼得森图为 k = 5,e = 15,v = 10,这样 2 ( 2) − − k k v e 不成立, 所以彼得森图非平面图。(3 分) 二、 逻辑推演 16% 1、 证明: ① A P(附加前提) ② A B T①I ③ A B →C D P ④ C D T②③I ⑤ D T④I ⑥ D E T⑤I ⑦ D E → F P ⑧ F T⑥⑦I ⑨ A → F CP 2、证明 ① xP(x) P(附加前提) ② P(c) US① ③ x(P(x) → Q(x)) P ④ P(c) → Q(c) US③

60105dfca3d04de78d0fae2fb259d7ed.doc ⑤Q(c) T②④I ⑥xQx) UG⑤ ⑦VxPx)→VxQ(x) CP 三、计算18% 1、解: 010 0 1010 101 0 0101 MR= 0 00 1 Me =MRoMR= 0000 0000 0000 0101 1010 Me=MeMR= 0000 000 0 1010 1111 0101 1111 Me =MRoMR= 0000 MI(R)=MR+Me +Me+Me 0001 0000 0000 .t(R)={<a,a>,<a,b>,<a,>,<a,d>,<b,a>,<b,b>,<b,c.>, <b,d>,<c,d>} 2、解:用库斯克(Kruskal)算法求产生的最优树。算法略。结果如图: 1 2 23 V6 9 9W3 V7 5174 树权C(T=23+1+4+9+3+17=57即为总造价。 8
60105dfca3d04de78d0fae2fb259d7ed.doc 8 ⑤ Q(c) T②④I ⑥ xQ(x) UG⑤ ⑦ xP(x) → xQ(x) CP 三、 计算 18% 1、 解: = 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 M R , = = 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 M R 2 M R M R = = 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 M R 3 M R 2 M R , = = 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 M R 4 M R 3 M R = + + + = 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 3 4 Mt(R) M R M R M R M R t (R)={<a , a> , <a , b> , < a , c> , <a , d > , <b , a > , < b ,b > , < b , c . > , < b , d > , < c , d > } 2、 解: 用库斯克(Kruskal)算法求产生的最优树。算法略。结果如图: 树权 C(T)=23+1+4+9+3+17=57 即为总造价