
握手定理 在无向图G=<V,E>中,则所有结点的度数的总和等于边 数的两倍,即: ∑deg(v))=2m; VeV 2.在有向图G=<V,E>中,则所有结点的引出度数之和等 于所有结点的引入度数之和,所有结点的度数的总和 等于边数的两倍,即: ∑deg*(w)=∑deg(w)=m, v deg(v)->deg"(v)+deg (v)=2m. 2025/5/13 计算机与信息工程学院
2025/5/13 计算机与信息工程学院 11 握手定理 在无向图G=<V,E>中,则所有结点的度数的总和等于边 数的两倍,即: deg(v) 2m; v V = deg (v) deg (v) m, v V v V = = − + 2. 在有向图G=<V,E>中,则所有结点的引出度数之和等 于所有结点的引入度数之和,所有结点的度数的总和 等于边数的两倍,即: deg(v) deg (v) deg (v) 2m。 v V v V v V = + = − +

推论 在图G=<V,E>中,其V={V1,v2,3,Vn},E= {e1,e2,em},度数为奇数的结点个数为偶数。 证明设V={vlvEVJ且deg(w)=奇数},V2={vlveV.且 deg(v)=偶数}。显然,V1∩V2=Φ,且V1UV2=V,于是 有: ∑degv)=∑deg(v)+∑deg(v)=2mo vEV vEV? 由于上式中的2m和(偶数之和为偶数)均为偶数,因而也 为偶数。于是IV1l为偶数(因为V,中的结点v之degw)都 为奇数),即奇度数的结点个数为偶数。■ 2025/5/13 计算机与信息工程学院 12
2025/5/13 计算机与信息工程学院 12 推论 在图G=<V,E>中,其V={v1,v2,v3,.,vn},E= {e1,e2,.,em},度数为奇数的结点个数为偶数。 证明设V1={v|vV且deg(v)=奇数},V2={v|vV且 deg(v)=偶数}。显然,V1∩V2=Φ,且V1∪V2=V,于是 有: deg(v) deg(v) deg(v) 2m。 v V v V1 v V2 = + = 由于上式中的2m和(偶数之和为偶数)均为偶数,因而也 为偶数。于是|V1|为偶数(因为V1中的结点v之deg(v)都 为奇数),即奇度数的结点个数为偶数。■
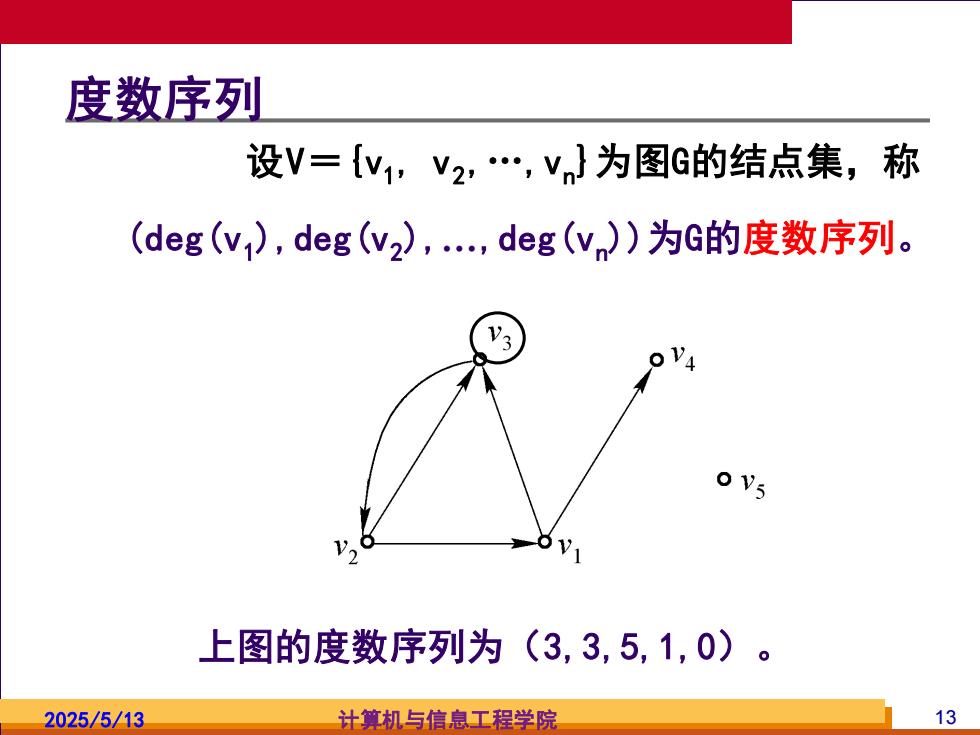
度数序列 设V=V1,V2,.,vn}为图G的结点集,称 (deg(v),deg(v2),deg(v)为G的度数序列。 ● 0V5 上图的度数序列为(3,3,5,1,0)。 2025/5/13 计算机与信息工程学院 13
2025/5/13 计算机与信息工程学院 13 度数序列 设V={v1 , v2 , .,vn }为图G的结点集,称 (deg(v1 ),deg(v2 ),.,deg(vn ))为G的度数序列。 上图的度数序列为(3,3,5,1,0)

例 (3,3,2,3),(5,2,3,1,4)能成为图的度数序列吗? 为什么? 解由于这两个序列中,奇数的个数均为奇数,由握手 定理的推论知,它们都不能成为图的度数序列。 2025/5/13 计算机与信息工程学院 14
2025/5/13 计算机与信息工程学院 14 (3,3,2,3),(5,2,3,1,4)能成为图的度数序列吗? 为什么? 例 解 由于这两个序列中,奇数的个数均为奇数,由握手 定理的推论知,它们都不能成为图的度数序列

子图与补图 定义6.7设有图G=<V,E>和图G'=<V,E>。 若V'∈V,E'∈E,则称G'是G的子图,记为G'∈G。 若V'=V,E'cE,则称G'是G的生成子图。 2025/5/13 计算机与信息工程学院 15
2025/5/13 计算机与信息工程学院 15 子图与补图 定义6.7 设有图G=<V,E>和图G'=<V',E'>。 若V'V,E'E,则称G'是G的子图,记为G'G。 若V'=V,E'E,则称G'是G的生成子图