
图的分类(按边的重数) 在有向图中,两个结点间(包括结点自身间)若有同始点 和同终点的几条边,则这几条边称为平行边, 在无向图中,两个结点间(包括结点自身间)若有几条边, 则这几条边称为平行边; 两结点v1,v间相互平行的边的条数称为边(v1,v)或<v, v>的重数; 含有平行边的图称为多重图; 非多重图称为线图; 无自回路的线图称为简单图。 2025/5/13 计算机与信息工程学院 6
2025/5/13 计算机与信息工程学院 6 在有向图中,两个结点间(包括结点自身间)若有同始点 和同终点的几条边,则这几条边称为平行边, 在无向图中,两个结点间(包括结点自身间)若有几条边, 则这几条边称为平行边; 两结点vi,vj间相互平行的边的条数称为边(vi,vj)或<vi, vj>的重数; 含有平行边的图称为多重图; 非多重图称为线图; 无自回路的线图称为简单图。 图的分类(按边的重数)
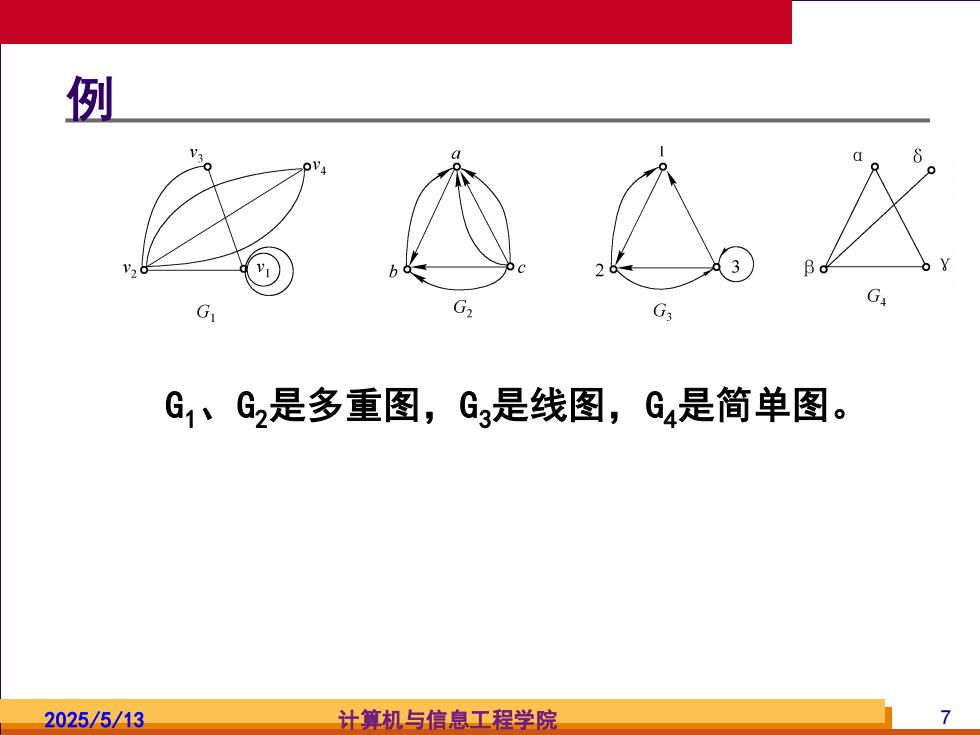
例 G G G1、G2是多重图,G是线图,G4是简单图。 2025/5/13 计算机与信息工程学院
2025/5/13 计算机与信息工程学院 7 例 G1、G2是多重图,G3是线图,G4是简单图

图的分类(按权) 定义6.5赋权图G是一个三元组<V,E,g>或四元组 N,E,f,g>,其中V是结点集合,E是边的集合,f是从V到 非负实数集合的函数,g是从E到非负实数集合的函数。 非赋权图称为无权图。 50 9 6 6 40 8 9 10 70 35 G G2 2025/5/13 计算机与信息工程学院 8
2025/5/13 计算机与信息工程学院 8 定义6.5 赋权图G是一个三元组<V,E,g>或四元组 <V,E,f,g>,其中V是结点集合,E是边的集合,f是从V到 非负实数集合的函数,g是从E到非负实数集合的函数。 非赋权图称为无权图。 图的分类(按权)

2结点的度数 在无向图G=<W,E>中,与结点v(vEV)关联的边的条(有 环时计算两次),称为该结点的度数,记为deg(w); 在有向图G=<W,E>中,以结点v为始点引出的边的条数, 称为该结点的出度,记为deg(v);以结点v为终点引 入的边的条数,称为该结点的入度,记为deg(v);而 结点的引出度数和引入度数之和称为该结点的度数, 记为deg(v),即deg(w)=deg*(v)+deg(v); 对于图G=<N,E>,度数为1的结点称为悬挂结点,它所 关联的边称为悬挂边。 在图G=<V,E>中,称度数为奇数的结点为奇度数结点, 度数为偶数的结点为偶度数结点。 2025/5/13 计算机与信息工程学院
2025/5/13 计算机与信息工程学院 9 在无向图G=<V,E>中,与结点v(vV)关联的边的条(有 环时计算两次),称为该结点的度数,记为deg(v); 在有向图G=<V,E>中,以结点v为始点引出的边的条数, 称为该结点的出度,记为deg+(v);以结点v为终点引 入的边的条数,称为该结点的入度,记为deg-(v);而 结点的引出度数和引入度数之和称为该结点的度数, 记为deg(v),即deg(v)=deg+(v)+deg-(v); 对于图G=<V,E>,度数为1的结点称为悬挂结点,它所 关联的边称为悬挂边。 在图G=<V,E>中,称度数为奇数的结点为奇度数结点, 度数为偶数的结点为偶度数结点。 2 结点的度数
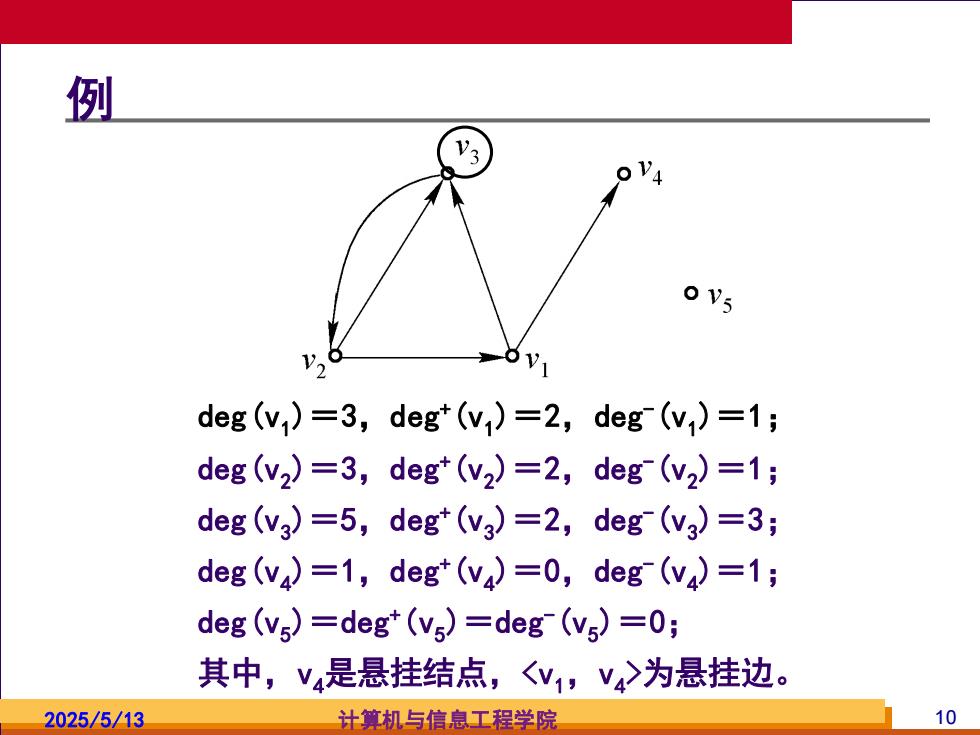
例 o vs 1V deg (v)=3,deg*(v)=2,deg(v)=1; deg(v2)=3,deg*(v2)=2,deg(v2)=1; deg(g)=5,deg*(v3)=2,deg(v3)=3; deg(v4)=1,deg(v4)=0,deg(v4)=1; deg (vs)=deg*(vs)=deg-(vs)=0; 其中,V4是悬挂结点,V1,V4>为悬挂边。 2025/5/13 计算机与信息工程学院 10
2025/5/13 计算机与信息工程学院 10 deg(v1 )=3,deg+(v1 )=2,deg-(v1 )=1; 例 deg(v2 )=3,deg+(v2 )=2,deg-(v2 )=1; deg(v3 )=5,deg+(v3 )=2,deg-(v3 )=3; deg(v4 )=1,deg+(v4 )=0,deg-(v4 )=1; deg(v5 )=deg+(v5 )=deg-(v5 )=0; 其中,v4是悬挂结点,<v1,v4 >为悬挂边