例 Q G G G 在如图中,给出了图G以及它的子图G'和 生成子图G“。 显然,每个图都是它自身的子图。 2025/5/13 计算机与信息工程学院 16
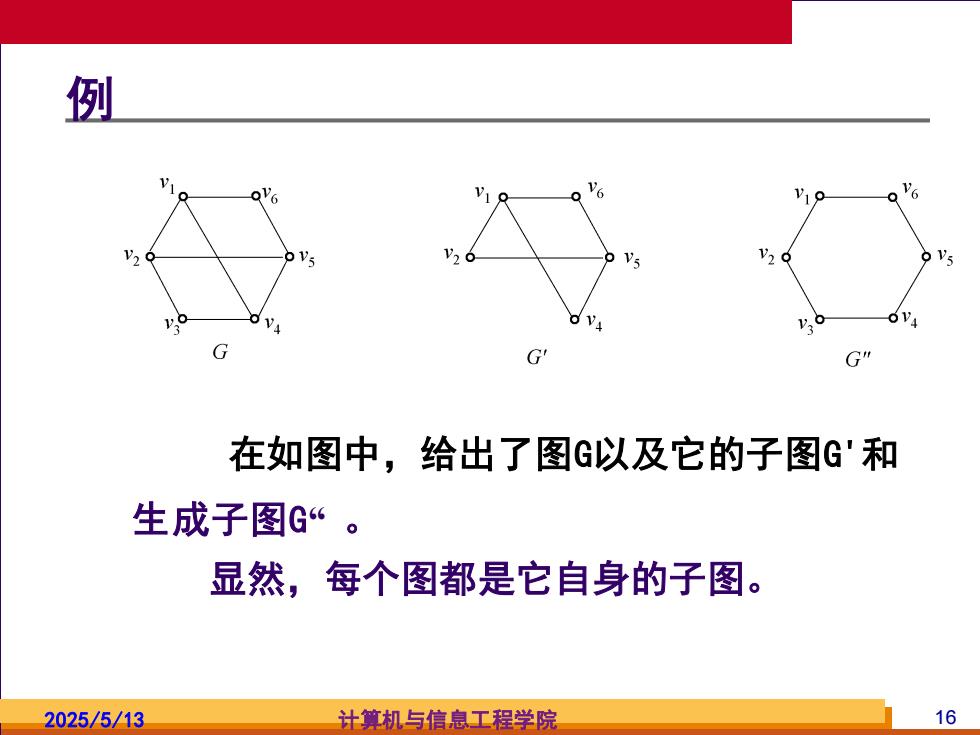
2025/5/13 计算机与信息工程学院 16 例 在如图中,给出了图G以及它的子图G'和 生成子图G“ 。 显然,每个图都是它自身的子图

完全图 设G=<W,E>为一个具有n个结点的无向简单图, 如果G中任一个结点都与其余-1个结点相邻 接,则称G为无向完全图,简称G为完全图, 记为K。 设G=<W,E>为一个具有n个结点的有向简单图, 若对于任意u,veV(uw),既有有向边<u,v>, 又有有向边<v,u>,则称G为有向完全图,在 不发生误解的情况下,也记为K 无向完全图K的边数为c2=二n(n-1),有向完全 图K的边数为P=n(n-1)。 2025/5/13 计算机与信息工程学院 17
2025/5/13 计算机与信息工程学院 17 完全图 设G=<V,E>为一个具有n个结点的无向简单图, 如果G中任一个结点都与其余n-1个结点相邻 接,则称G为无向完全图,简称G为完全图, 记为Kn。 设G=<V,E>为一个具有n个结点的有向简单图, 若对于任意u,vV(uv),既有有向边<u,v>, 又有有向边<v,u>,则称G为有向完全图,在 不发生误解的情况下,也记为Kn。 无向完全图Kn的边数为 = n(n-1),有向完全 图Kn的边数为 Pn 2 = n(n-1)。 2 Cn 2 1
例 无向的简单完全图K,K4,K和有向的简单 完全图K3 2025/5/13 计算机与信息工程学院 18
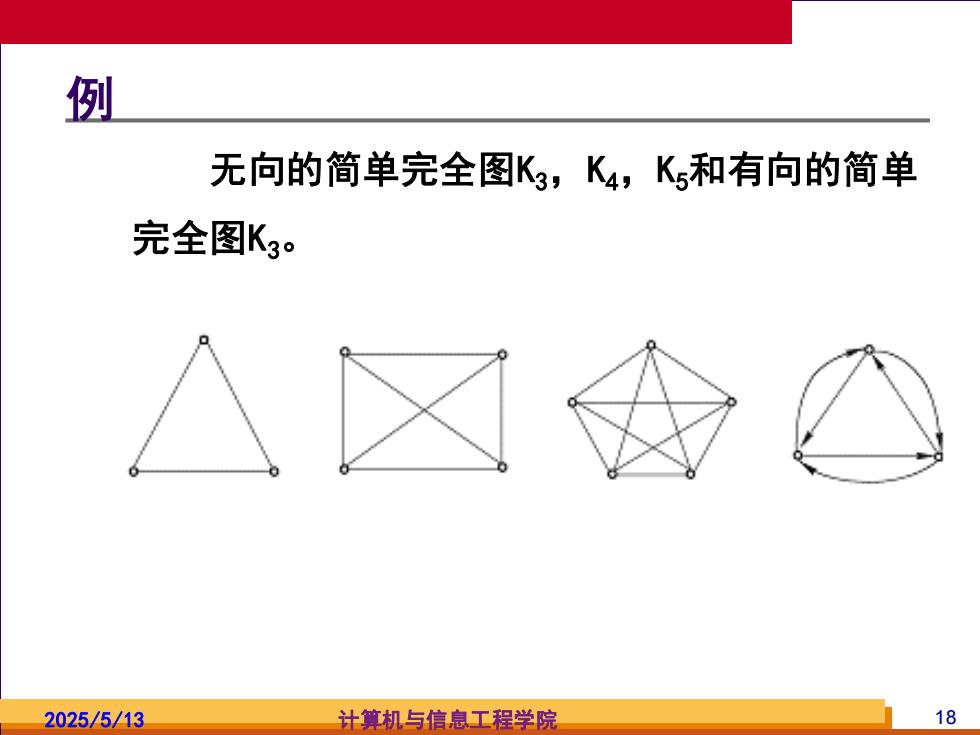
2025/5/13 计算机与信息工程学院 18 例 无向的简单完全图K3,K4,K5和有向的简单 完全图K3

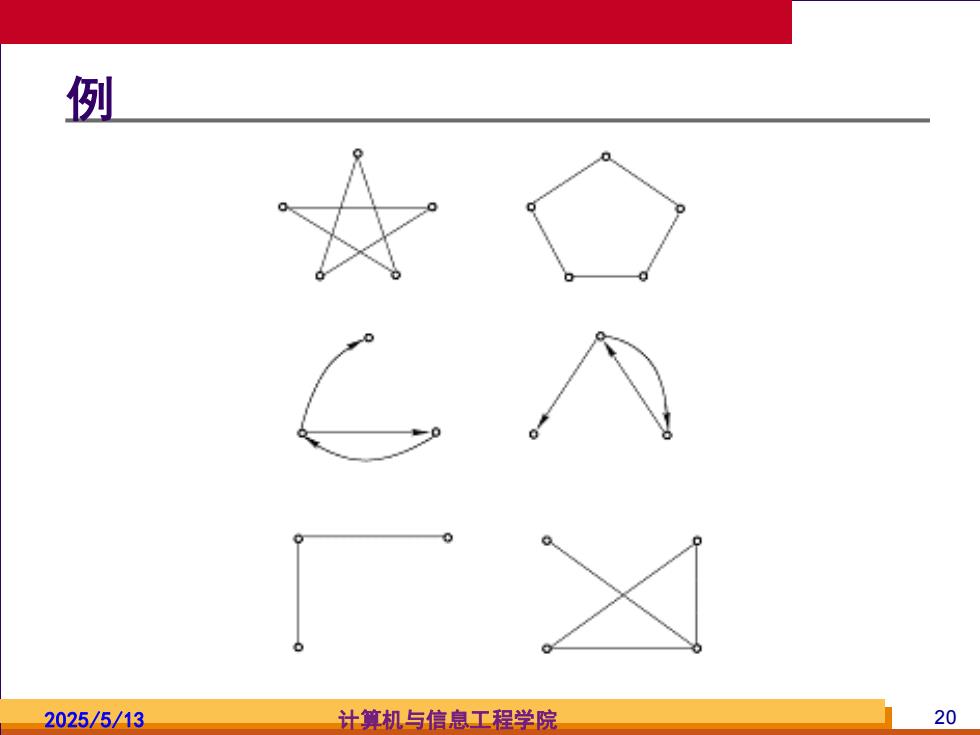
定义补图 设G=<W,E>为具有n个结点的简单图, 从完全图K中删去G中的所有边而得到的图 称为G相对于完全图K的补图,简称G的补 图,记为G。 这里,当G为有向图时,则K为有向完 全图:当G为无向图时,则K为无向完全图 显然,G与G互为补图,即G=G。 2025/5/13 计算机与信息工程学院 19
2025/5/13 计算机与信息工程学院 19 定义补图 设G=<V,E>为具有n个结点的简单图, 从完全图Kn中删去G中的所有边而得到的图 称为G相对于完全图Kn的补图,简称G的补 图,记为G。 这里,当G为有向图时,则Kn为有向完 全图:当G为无向图时,则Kn为无向完全图 显然,G与G互为补图,即G=G
例 2025/5/13 计算机与信息工程学院 20
2025/5/13 计算机与信息工程学院 20 例