
O00001无穷小R人邮教育有限个无穷小的代数和是无穷小性质1.1注无穷多个无穷小的代数和不一定是无穷小12n中每一项均为无穷小,tLn2+n+1n2+n+2n2+n+n121n但lim(FLX2+n+l+n+2n+n+nNRn21110ae1limnc+L +n? +2pn?+np 0n??2+pen
注 6 无穷多个无穷小的代数和不一定是无穷小. 中每一项均为无穷小, 但 . 01 无穷小 性质1.1 有限个无穷小的代数和是无穷小
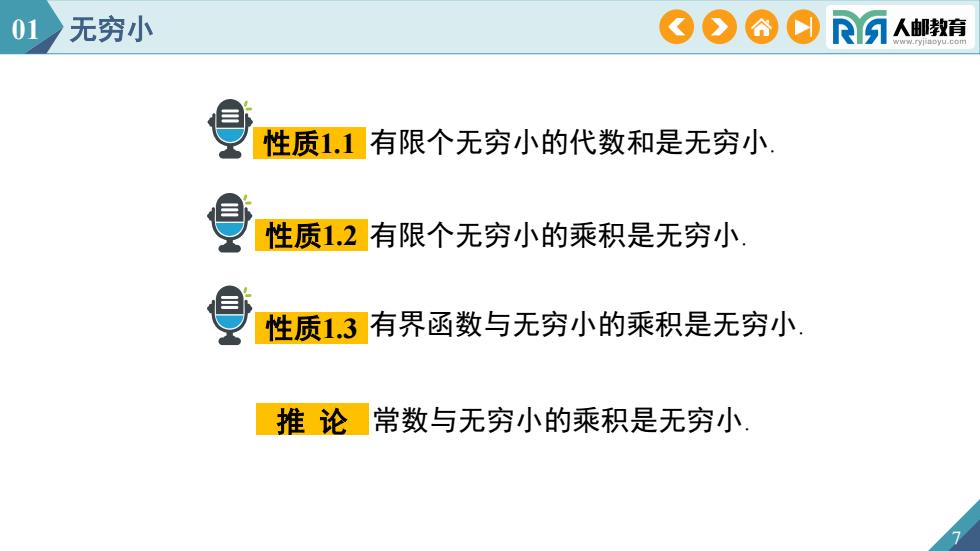
无穷小CO001R人邮教育有限个无穷小的代数和是无穷小性质1.1性质1.2有限个无穷小的乘积是无穷小有界函数与无穷小的乘积是无穷小性质1.3推论常数与无穷小的乘积是无穷小
性质1.1 性质1.2 性质1.3 推 论 7 有限个无穷小的代数和是无穷小. 有限个无穷小的乘积是无穷小. 有界函数与无穷小的乘积是无穷小. 常数与无穷小的乘积是无穷小. 01 无穷小

CO001无穷小人邮教育RA例3求极限limxSin -X?0x由于解O1, x1 0,sin故sin一在x=0的任意去心邻域内是有界的而x2是x?0时x的无穷小,由性质1.3可知,x2sin二是x0时的无穷小,即x1limx sin = = 0.x?0x
8 求极限: 解 由于 例 3 01 无穷小 故 在 的任意去心邻域内是有界的. 而 是 时 的无穷小,由性质1. 3 可知, 是 时的无穷小,即

O0ARA人邮教育思考:sinx1.limXR?x2. lim x sinXR?x13.lim x sin -x0x
9 思考:

R人邮教育本讲内容w.yjinaoyu.cc01无穷小量02无穷大量03无穷小量的比较04等价无穷小代换
01 无穷小量 02 无穷大量 03 无穷小量的比较 04 等价无穷小代换 本 讲 内 容