
u= f(x,y),例2设函数u(x)由方程组g(x,y,z) = 0.h(x,z) = 0.ahogdu所确定,且#0, 求±0Ozoydx分析变量4个,方程3个独立自变量1个.由题意选x为独立自变量.则u=u(x),y= (x),z= z(x)解 法一方程组各方程两边微分,得du = f,dx + f,dydx + g,dz)gdx + g,dy + g,dz = 0= dy =gyh.dx + h.dz = 0hdx.dz川D
= = = ( , ) 0. ( , , ) 0, ( , ), ( ) h x z g x y z u f x y 设函数 u x 由方程组 解 例2 法一 方程组各方程两边微分, 得 u f x f y d = xd + yd gxdx + gydy + gzdz = 0 hxdx + hzdz = 0 d dx. h h z z x = − ( d d ) 1 d g x g z g y x z y = − + 分析 变量4个,方程3个, 则u = u(x), y = y(x),z = z(x) , 0, 0, z h y g 所确定 且 . d d x u 求 独立自变量1个.由题意 选x为独立自变量.

u= f(x,y),得法二方程组各方程两边对x求导,g(x, y,z)= 0dudy(1)h(x,z)=0.XLdxdxdzdy(2)0gx+gy+gzdxdxdz(3)h0xdxdy_g,·hxhydzgx代入(2)得由(3)得dxg,·hzgydxMS,g,-h.dufy'gx代入(1)得?dxg,-h,gy
= x u d d 由(3)得 代入(2)得 代入(1)得 法二 = = = ( , ) 0. ( , , ) 0, ( , ), h x z g x y z u f x y 方程组各方程两边对x求导, 得 gx hx , d d z x h h x z = − , d d y x y z z x g g g h g h x y − = . d d y z y z x y y x x g h f g h g f g f x u + = − x f x y f y d d + (1) x y gy d d + x z gz d d + = 0 (2) x z hz d d + = 0 (3)
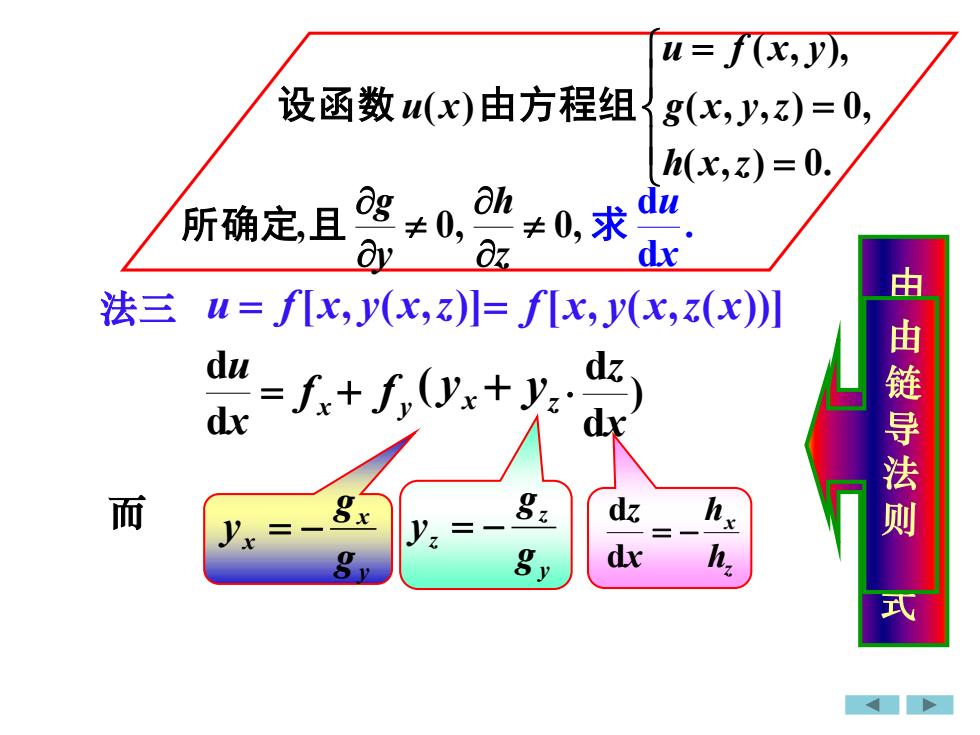
u= f(x,y),设函数u(x)由方程组g(x, y,z) = 0h(x,z) = 0.ahduag#0,求所确定,且±0.az.avdx由日由链导法则法三u= f[x, y(x,z)]= f[x, y(x,z(x)duf+ f,(yx+ y)dxdxg.gx而hdzxVVZX公dxg911式
法三 u = f[x, y(x,z)]= f[x, y(x,z(x))] = x u d d 而 y x x g g y = − y z z g g y = − z x h h x z = − d d y + f z + y = = = ( , ) 0. ( , , ) 0, ( , ), ( ) h x z g x y z u f x y 设函数 u x 由方程组 , 0, 0, z h y g 所确定 且 . d d x u 求 x f x ( y ) d d x z