
(4)均值: 1)简单平均x N 2)加权平均x-三x,其中Σ了,=1 N 3)调和平均H” 三 公为 4)加权调和平均 H 5几何平均G,=XXX 返回
返回 (4)均值: 1)简单平均 2)加权平均 3)调和平均 4)加权调和平均 5)几何平均 N X X N i i 1 , 1 N i i X i X f 1 1 N i i f N i X M i N H 1 1 N i Xm N i i M i i m H 1 1 N GM X1X2XN 其中
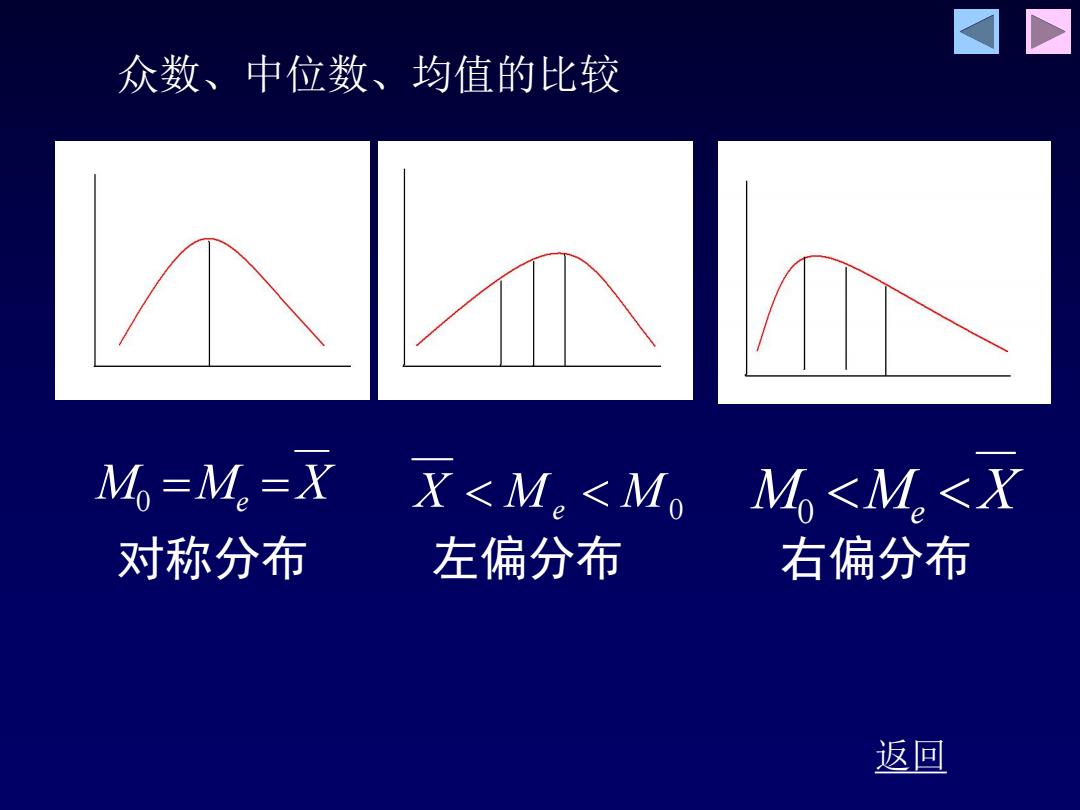
众数、中位数、均值的比较 Mo=M.=X X<M。<M。M<M<X 对称分布 左偏分布 右偏分布 返回
返回 众数、中位数、均值的比较 对称分布 左偏分布 右偏分布 M0 Me X X Me M0 M0 Me X

2、分布的离散程度: (1)平均离差 M- 三x,-7 N (2) 样本方差 立(x-x N-1 (3)样本标准差 x-列 =1 N-1 (4)极差 maxX,-minX 返回
返回 2、分布的离散程度: (1) (2) 平均离差 N X X M N i i D 1 样本方差 2 2 1 1 1 N i i n X X N (3) 样本标准差 2 1 1 1 N i i n X X N (4)极差 Xi m Xi max in

例:求1,2,3,4,5的样本均值,样本方差。 解: X= +2+3+4+5 =3, 5 g=1-3+2-3+3-3}+4-3}+5-3y 5-1 =2.5 返回
返回 例:求1,2,3,4,5的样本均值,样本方差。 2 2 2 2 2 2 1 2 3 4 5 3, 5 (1 3) (2 3) (3 3) (4 3) (5 3) 5 1 2.5 X 解:

第2.1节离散型随机变量及其分布 随机变量(random variables)概念 试验 考察 可能的结果 抛掷一枚硬币100次 正面出现的次数 0,1,2,..,100 家餐馆营业一天 顾客数 0,1,2, 抽查一批电子元件 使用寿命(小时) [0,+0o) 新建一座住宅楼 半年完成百分比 [0,100] 销售一辆汽车 顾客性别 男性为0,女性为1 t 记为5 {传=是一个随机事件。 返回
返回 试验 考察 可能的结果 抛掷一枚硬币100次 一家餐馆营业一天 抽查一批电子元件 新建一座住宅楼 销售一辆汽车 正面出现的次数 顾客数 使用寿命(小时) 半年完成百分比 顾客性别 0,1,2, …,100 0,1,2, … [0, ) [0, 100] 男性为0,女性为1 一 、随机变量 概念 记为 { k}是一个随机事件。 第2.1节 离散型随机变量及其分布