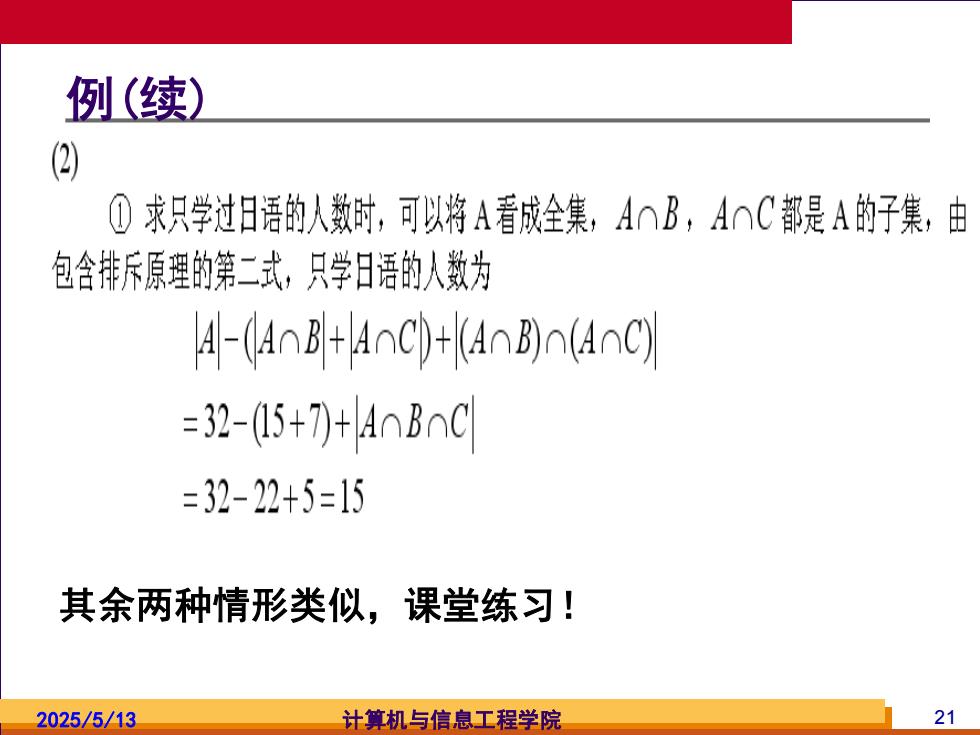
例(续) (2) ①求只学过日语的人数时,可以将A看成全集,AnB,AAC都是A的子集,由 包含排斥原理的第二式,只学日语的人数为 -(4n3+4nc)+(403)0(nC) =32-15+7)+AoBoC =32-22+5=15 其余两种情形类似,课堂练习! 2025/5/13 计算机与信息工程学院 21
2025/5/13 计算机与信息工程学院 21 例(续) 其余两种情形类似,课堂练习!

(3)对(AnB),(A∩C,(BAC)用包含排斥原理的第一式,得至少学过两种语言 的人数为 (40B)(4nC)(BoC) 40+4nC+Boc-340B0C+4nBnc =7+15+10-3x5+5=22 4)由于A∩B∩C是(AnB),(AnC)和(B∩C)的子集。所以只学过日语和法语、 日语和英语、法语和英语的人数分别为 40B-40BoC=7-5=2 40C-40BoC=15-5=10 BoC-4nBnC =7-5=2 可考虑文氏图方法解决。 2025/5/13 计算机与信息工程学院 22
2025/5/13 计算机与信息工程学院 22 可考虑文氏图方法解决

3笛卡儿积与关系 一、序偶与笛卡尔积 1、序偶的定义 定义3.3.1由两个元素x,y按照一定的次序 组成的二元组称为序偶,记作<x,y>,其中x为 第一个元素,y为第二个元素。 2025/5/13 计算机与信息工程学院 23
2025/5/13 计算机与信息工程学院 23 3 笛卡儿积与关系 一、序偶与笛卡尔积 1、序偶的定义 定义3.3.1 由两个元素x,y按照一定的次序 组成的二元组称为序偶,记作<x,y>,其中x为 第一个元素,y为第二个元素

1.序偶<x,y>中的两个元素不一定来自同一集合 2.序偶中的两个元素具有确定的次序。即 <a,b>≠<b,a>但是{a,b}={b,a}. 定义3.3.2两个序偶相等,<x,y>=<u,v>当且 仅当x=u,y=V。 2025/5/13 计算机与信息工程学院 24
2025/5/13 计算机与信息工程学院 24 定义3.3.2 两个序偶相等,<x,y>=<u,v>当且 仅当x=u,y=v。 1. 序偶<x,y>中的两个元素不一定来自同一集合 2. 序偶中的两个元素具有确定的次序。即 <a,b>≠<b,a>但是{a,b}={b,a}

2、笛卡尔乘积 定义设A,B是两个集合,称下述集合: AXB={Kx,y>|(x∈A)∧(y∈B)} 为由A,B构成的笛卡尔乘积。 例1已知A={0,1,2},B={a,b},计算AXB和B×A。 解:AXB={<0,a>,<1,a>,<2,a>,<0,b>,<1,b>,2,b>} B×A={Ka,0>,<a,1>,<a,2>,<b,0>,<b,1>,<b,2>} 显然有 AXB≠BXA 2025/5/13 计算机与信息工程学院 25
2025/5/13 计算机与信息工程学院 25 2、笛卡尔乘积 定义设A,B是两个集合,称下述集合: A×B={<x,y>|(x∈A)∧(y∈B)} 为由A,B构成的笛卡尔乘积。 例 1 已知A={0,1,2},B={a,b},计算A×B和B×A。 解:A×B={<0,a>,<1,a>,<2,a>,<0,b>,<1,b>,<2,b>} B×A={<a,0>,<a,1>,<a,2>,<b,0>,<b,1>,<b,2>} 显然有 A×B≠B×A