
例 1)设A={2,4,6,8},B={xk是正偶数}, C={xx是整数},则有A∈B,BC, AcC,并且AcB,BcC,AcC。 2)A如上定义,A有几个子集? 2025/5/13 计算机与信息工程学院 6
2025/5/13 计算机与信息工程学院 6 1) 设A={2,4,6,8} ,B= {x|x是正偶数}, C={x|x是整数},则有A B,B C, AC,并且A B,B C,A C 。 2) A如上定义, A有几个子集? 例

重要结论 1)对任意集合A,有ACA。 2)空集是任意集合的子集,且空集是唯一的。(如何 证明?) 3)对于任意两个集合A、B,A=B的充要条件是ACB 且BcA。 4)集合与集合之间是包含与否,元素与集合之间是属 于与否。 2025/5/13 计算机与信息工程学院
2025/5/13 计算机与信息工程学院 7 1)对任意集合A, 有A A。 2)空集是任意集合的子集,且空集是唯一的。(如何 证明?) 3)对于任意两个集合A、B,A=B的充要条件是AB 且BA。 4)集合与集合之间是包含与否,元素与集合之间是属 于与否。 重要结论

有限集、幂集power set 称含有限个元素的集合为有穷集。用A表示A中 的元素个数。若A=n,则称A为n元集。(集合元 素个数也叫基数、势) n元集合的k元子集有几个? 设A为一个集合,称A的全部子集组成的集合为 的幂集,P(A)或2A n元集合A的幂集有多少元素? 2025/5/13 计算机与信息工程学院 8
2025/5/13 计算机与信息工程学院 8 有限集、幂集power set 称含有限个元素的集合为有穷集。用|A|表示A中 的元素个数。若|A|=n,则称A为n元集。(集合元 素个数也叫基数、势) n元集合的k元子集有几个? 设A为一个集合,称A的全部子集组成的集合为 的幂集, P(A) 或 2 A n元集合A的幂集有多少元素?

例 例5.1.1设A={☑},0,1},计算A的幂集。 解:P(A)={☑, {☑},{0},{1}, {0,{☑},{1,{0},{0,1}, {☑},0,1}} 例5.1.2证明AcB的充要条件P(A)cP(B)。 证明: 充分性。 Vx∈A,有{x}cA。由P(A)cP(B)有{x}CB,所以x∈B, 即AcB。 必要性。 VC∈P(A),有CcA。因为AcB,所以CcB。因此C∈P(B)。 即P(A)cP(B)。 2025/5/13 计算机与信息工程学院 9
2025/5/13 计算机与信息工程学院 9 例 例5.1.1 设A={{},0,1},计算A的幂集。 解:P(A)= {, {{}},{0},{1}, {0,{}},{1,{}},{0,1}, {{},0,1} } 例5.1.2 证明AB的充要条件P(A)P(B)。 证明: 充分性。 xA,有{x}A。由P(A)P(B)有{x}B,所以xB, 即 AB。 必要性。 CP(A),有CA。因为AB,所以CB。因此CP(B)。 即 P(A)P(B)
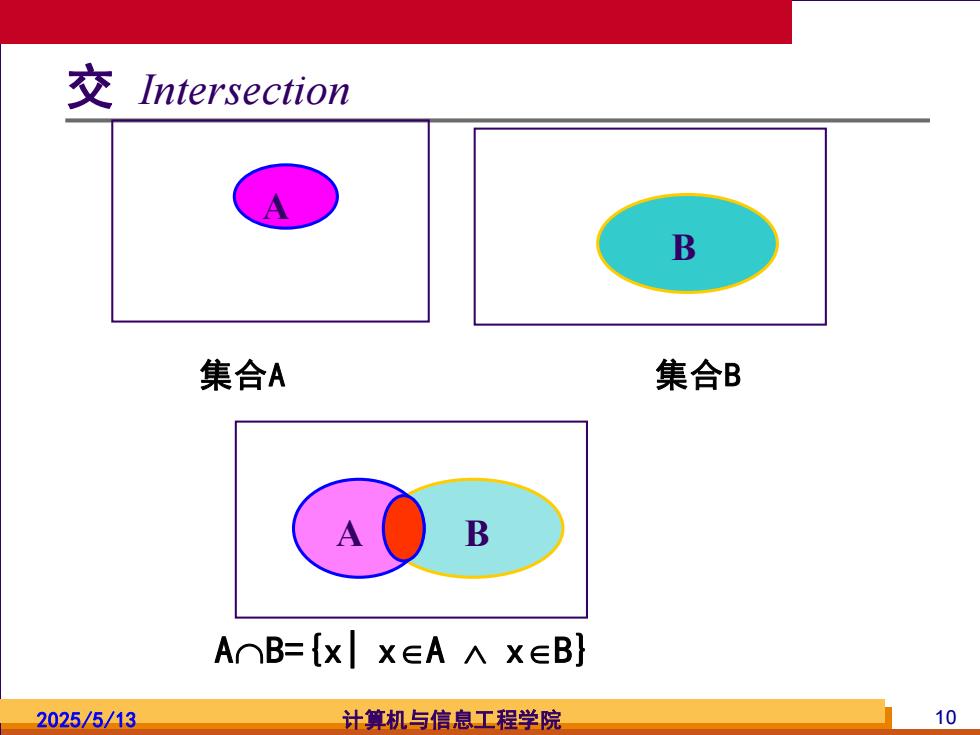
交 Intersection B 集合A 集合B B AOB={xX∈AAX∈B} 2025/5/13 计算机与信息工程学院 10
2025/5/13 计算机与信息工程学院 10 交 Intersection AB={x| xA xB} A B A B 集合A 集合B