割线与切线 第二章 一元函数微分学及其应用 设曲线C:y=f(x),x∈I,在曲线C上取点M(,)及点N(x,y), 连接N,则N为过点M的割线,割线的倾角为p(见图2-6). 则割线MN的斜率为 tano=>-f(x)-f(x) y=f(x N x-Xo x-Xo M 图2-6 导数的几何意义 6
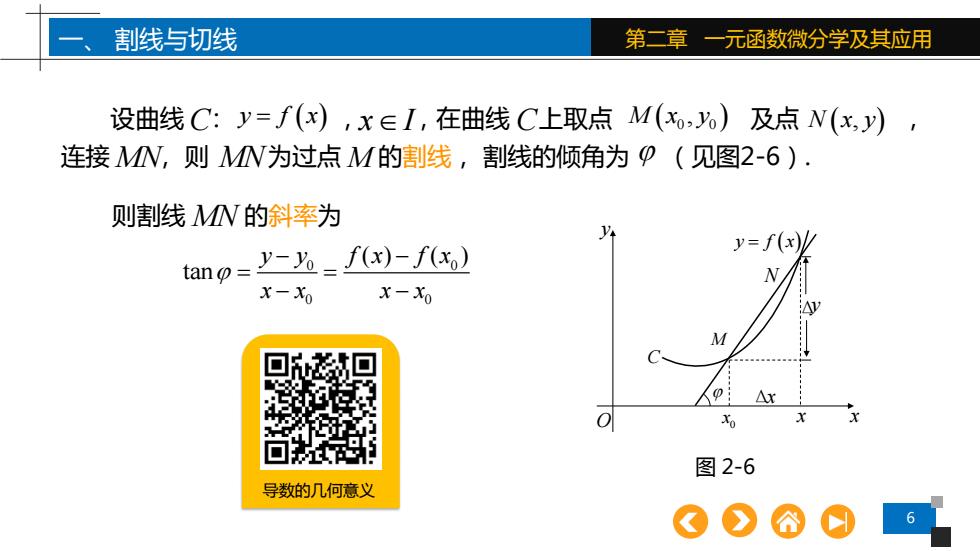
6 一、 割线与切线 第二章 一元函数微分学及其应用 设曲线 : , ,在曲线 上取点 及点 , 连接 , 则 为过点 的割线, 割线的倾角为 (见图2-6). C y f x = ( ) x I C M x y ( 0 0 , ) N x y ( , ) MN MN M 0 0 0 0 ( ) ( ) tan y y f x f x x x x x − − = = − − 则割线 MN 的斜率为 y O x C M N y f x = ( ) 0 x x Δy Δx 图 2-6 导数的几何意义
割线与切线 第二章一元函数微分学及其应用 当N→M,即x→x,时,如果割线趋于一极限位置,我们就把此极限 位置上的直线MT称为曲线在M点处的切线 y=f(x)/ 此刻切线的斜率即为k=limy-必=lim f(x)-f(x) →0X-X0x→0 x-Xo M 从上面的例子可以看出,在求切线斜率的过 程中,需要用到极限 lim f(x)-f(x.) x→x0 X-Xo 图2-6
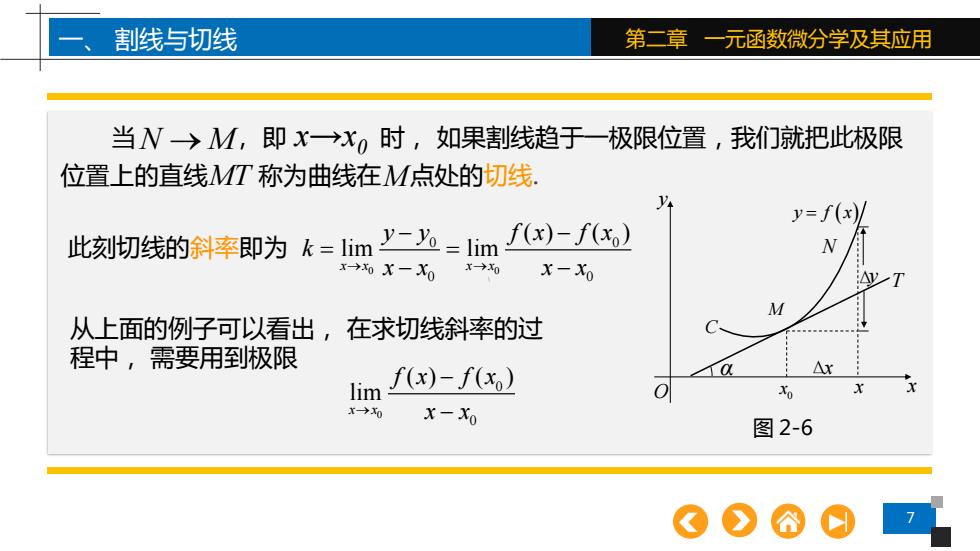
7 一、 割线与切线 第二章 一元函数微分学及其应用 0 0 0 0 0 0 ( ) ( ) lim lim x x x x y y f x f x k → → x x x x − − = = − − 从上面的例子可以看出, 在求切线斜率的过 程中, 需要用到极限 0 0 0 ( ) ( ) lim x x f x f x → x x − − 当 , 即 时, 如果割线趋于一极限位置,我们就把此极限 位置上的直线 称为曲线在 点处的切线. x→x N M → 0 MT M 此刻切线的斜率即为 y O x C M N y f x = ( ) T α 0 x x Δy Δx 图 2-6

二 导数的定义 第二章一元函数微分学及其应用 定义 设函数y=f(x)在x,的某个邻域内有定义,当x在x,处增量为△x (x。+△x在该邻域内)时,相应地,函数有增量△y=f(x+△x)-f(x)· 如果 lim Ay lim f(x+Ar)-f(%)=limf(x)-f(x) Ar-→0△x △r0 △x →0 x-Xo 存在,则称该极限为y=f(x)在点x,处的导数,记为 f),l或 8
8 二、导数的定义 第二章 一元函数微分学及其应用 定义 设函数 在 的某个邻域内有定义,当 在 处增量为 ( 在该邻域内)时,相应地, 函数有增量 . y f x = ( ) 0 x x 0 x x 0 x x + = + − y f x x f x ( 0 0 ) ( ) ( ) ( ) 0 0 0 0 0 0 0 ( ) ( ) lim lim lim x x x x y f x x f x f x f x → → → x x x x + − − = = − 存在,则称该极限为 y f x = ( ) 在点 x0 处的导数,记为 f x ( 0 ) , 0 x x y = 0 d d x x y x , = 或 0 d ( ) d x x f x x = 如果

导数的定义 第二章一元函数微分学及其应用 这时也称函数y=∫(x)在点x,处可导 如果该极限不存在,称函数y=∫(x)在点x,处不可导. 特别地,如果m化=0时,也称函数y=f()在点x处的导数为无旁大 △r0△x
9 二、导数的定义 第二章 一元函数微分学及其应用 这时也称函数 y f x = ( ) 在点 处可导. 0 x 如果该极限不存在,称函数 y f x = ( ) 在点 处不可导 . 0 x 特别地,如果 时,也称函数 在点 处的导数为无穷大. 0 lim x y → x = y f x = ( ) 0 x

二 导数的定义 第二章一元函数微分学及其应用 例如,对于函数y=x2,在点x=0处(见图2-7), lim y =lim (0+△x)}-0 =lim△x=0,极限存在 Ar→0△x △x0 △x △x0 图2-7 y=x 而对于函数yx,在点x=0处(见图2-8), lim Ay=lim 0+Ax-101-lim IAxl ar0△r 极限不存在. △x Ar0△x 由此可知,函数yx在x=0处不可导,而y=x2 图2-8 在x=0处导数为零,即 =0 10
10 二、导数的定义 第二章 一元函数微分学及其应用 例如,对于函数 在点 处(见图2-7), 2 y x = , x = 0 0 lim x y → x ( ) 2 0 0 0+ 0 = lim lim 0 x x x x → → x − = = ,极限存在. y x O 图 2-7 而对于函数 y x =| |, 在点 x = 0 处(见图2-8), 0 lim x y → x 0 0 |0+ | | 0 | | | = lim lim x x x x → → x x − = ,极限不存在. O x y 图 2-8 y x =| | 2 y x = 由此可知,函数 y x =| | 在 x=0 处不可导, 2 y x = x=0 0 d 0 d x x y x = = 而 在 处导数为零,即