
补例利用对称性简化计算 P1869(2). axdd Ω x2+y2+z2+1 其中积分区域2={x,y,川x2+y2+z2≤1. 解:积分域关于xoy坐标面对称 且被积函数是z的奇函数, +y++=0, x2+y+z2+1 0.5 0.5
补例 利用对称性简化计算 2 2 2 2 2 2 1 1 z x y z ln( ) dxdydz x y z + + + + + + 其中积分区域 2 2 2 = + + {( , , ) | } x y z x y z 1 . 解: 积分域关于xoy坐标面对称 且被积函数是 z 的奇函数, 2 2 2 2 2 2 1 0 1 ln( ) . z x y z dxdydz x y z + + + = + + + P186 9(2)
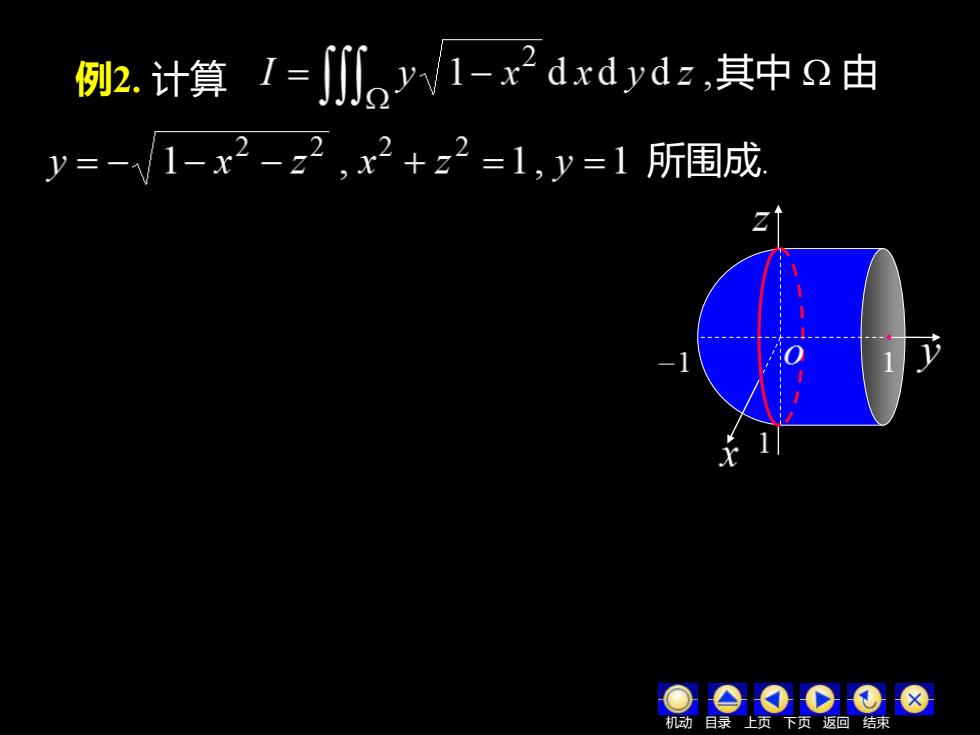
例2.计算I=j川0yW1-x2 dxdydz,其中2由 y=-1-x2-z2,x2+z2=1,y=1所围成 机动目录 上页下页返回结束
例2. 计算 所围成. 其中 由 机动 目录 上页 下页 返回 结束