二、三重积分的计算一化为三次积分 J∬。fx,)ay 1、利用直角坐标系计算三重积分. 方法1.投影法(“先一后二”) =(x,y) 如图:S:乙=(x,y), S S2:7=z2(x,y), (1)将闭区域2向x0y面上投影, (x,y) 得闭区域D; (2)过D内任一点(x,y)作垂直 于x0y面的直线, 与曲面S、S,交点的竖坐标 (x,y)∈D, 分别为(x,八2(x) 从而2: (x,y)≤3≤32(x,y)
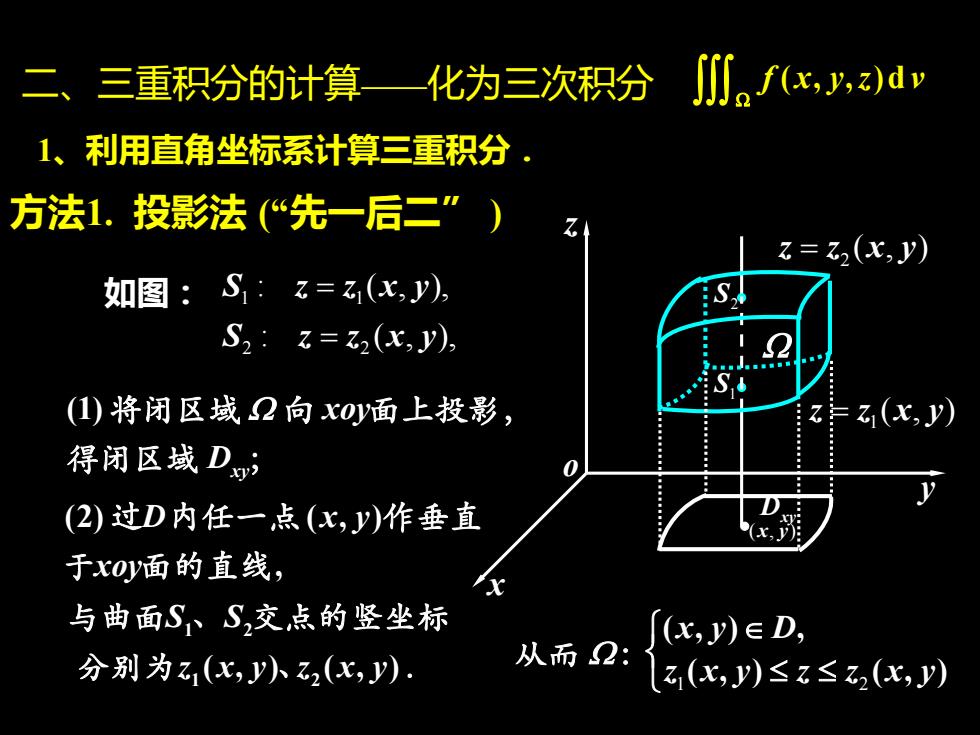
1、利用直角坐标系计算三重积分. 二、三重积分的计算——化为三次积分 x y z o S2 S1 Dxy ( , ) x y (1) xy xoy D 将闭区域 向 面上投影, 得闭区域 ; 1 1 2 2 : ( , ), : ( , ), S z z x y S z z x y = = (2) ( , ) , D x y xoy 过 内任一点 作垂直 于 面的直线 1 2 1 2 ( , ) ( , ) S S z x y z x y 与曲面 、 交点的竖坐标 分别为 、 . 从而 : 1 2 ( , ) , ( , ) ( , ) x y D z x y z z x y f x y z v ( , , )d 如图: 1 z z x y = ( , ) 2 z z x y = ( , ) 方法1. 投影法 (“先一后二” )

⊙)计算/x=Fx) z=2(x,) ④计算∬F(x,y)do D 即 ∬f(x,y,z)w= F(x,y) 7二 0 x施 do. y=y2(x) =∬F(x,y)do y=y(x) =Fc,海 2 f(x,y,z)d
2 1 ( , ) ( , ) ( , , ) z x y z x y f x y z dz [ ] . Dxy = d f x y z dv ( , , ) = 即 x y z o D 1 z z x y = ( , ) 2 z z x y = ( , ) a b 1 y y x = ( ) 2 y y x = ( ) ( , ) x y F x y ( , ) 2 1 ( , ) ( , ) ( , , ) z x y z x y f x y z dz (3) 计算 = F x y ( , ) (4) 计算 ( , ) . Dxy F x y d ( , ) . Dxy = F x y d 2 1 ( ) ( ) ( , ) . b y x a y x = dx F x y dy 2 2 1 1 ( ) ( , ) ( ) ( , ) ( , , ) . b y x z x y a y x z x y = dx dy f x y z dz

注:这是平行于z轴且穿过闭区域2内部的直线与闭区域 2的边界曲面S相交不多于两,点情形. 若积分域较复杂,可将它分成若干区域
z S 这是平行于 轴且穿过闭区域 内部的直线与闭区域 的边界曲面 相交不多于 注: 两点情形. 若积分域较复杂, 可将它分成若干区域

例1.计算三重积分川。xdxdyd=,.其中2为三个坐标 面及平面x+2y+:=1所围成的闭区域 0≤z≤1-x-2y 解:2:0≤y≤2(1-x) 0≤x≤1 xdxdyd= -xdx 1-x-2y)d 0(x-2x2+x3r= 48 练习:P167题 6 8
例1. 计算三重积分 d d d , 其中 为三个坐标 x x y z x + 2 y + z = 1 所围成的闭区域 . 1 x y z 1 2 1 解: : x d x d y d z − = − − (1 ) 0 1 0 2 1 d (1 2 )d x x x x y y −x− y z 1 2 0 d = − + 1 0 2 3 ( 2 )d 4 1 x x x x 0 z 1− x − 2 y 0 (1 ) 2 1 y − x 0 x 1 48 1 = 面及平面 练习: 机动 目录 上页 下页 返回 结束 P167题 6

补充:利用对称性化简三重积分计算 1、积分区域关于坐标面的对称性: 2、被积函数在积分区域上的关于三个变量的 奇偶性。 一般地,当积分区域2关于x0y平面对称时, (1)若被积函数f(x,y,z)是关于z的奇函数,则三重积分为零; (2)若被积函数f(x,y,z)是关于z的偶函数,则三重积分为Q 在x0y平面上方的半个闭区域的三重积分的2倍
补充:利用对称性化简三重积分计算 1、积分区域关于坐标面的对称性; 2、被积函数在积分区域上的关于三个变量的 一般地,当积分区域关于xoy平面对称时, (1)若被积函数 f ( x, y,z)是关于z的奇函数,则三重积分为零; (2)若被积函数 f ( x, y,z)是关于z的偶函数,则三重积分为 在xoy平面上方的半个闭区域的三重积分的 2 倍. 奇偶性.