《线性代数》课程PPT教学课件（同济第五版）第4章 向量组的线性相关性 4.5 线性方程组的解的结构

现对比+1，xn取下列n一r组数： X+1 x1=-b1+1-.-b1m-,xm 分别代入 x,=-b1x,+1-b,m-,x 上页

现对 x r+1 ,  , x n 取下列 n− r 组数：               + + n r r x x x  2 1      = − − − = − − − + − + − r r r r,n r n r ,n r n x b x b x x b x b x    1 1 1 1 1 1 1 分别代入 , .               1 0 0  ,               0 1 0  ,               = 0 0 1  

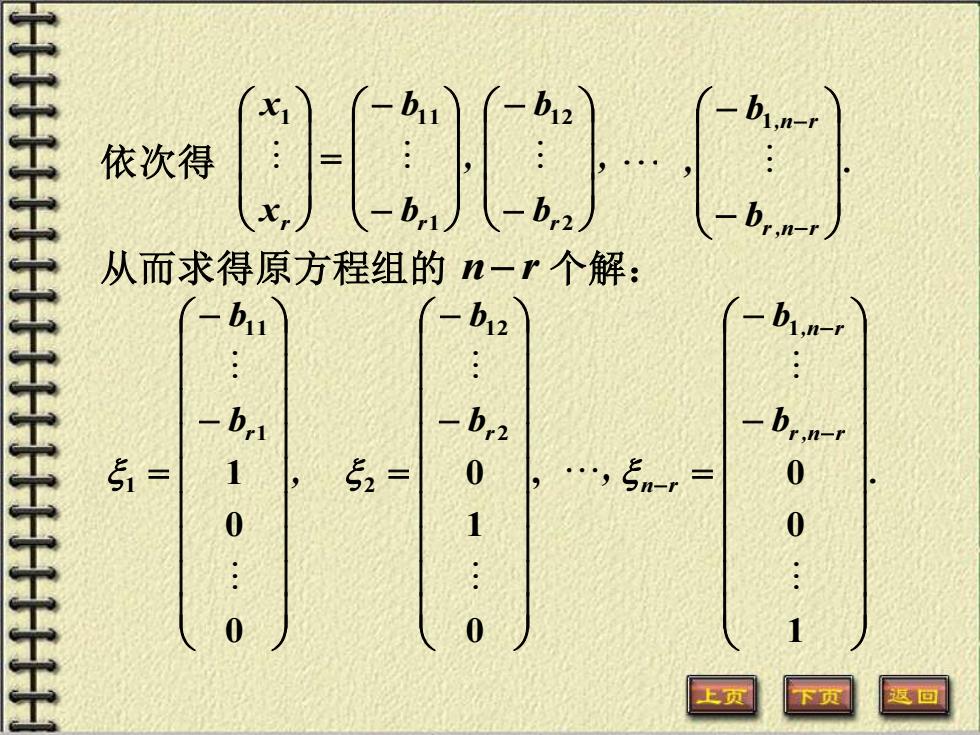
依次得 a 从而求得原方程组的n一r个解： b11 b1,n- b b,2 b:n 51= 52= 5m-= :0 0 1 上页 区回

依次得           xr x  1 , b b r                       − − = 0 0 1 1 11 1    , 0 1 0 2 12 2                       − − =   br b  . b b r,n r ,n r n r                       − − = − − − 1 0 0 1    从而求得原方程组的 n− r 个解： . b b , r,n r ,n r           − − − −  1 , b b r           − − 2 12 ,  b b r           − − = 1 11   

下面证明51,52，.，5m-,是齐次线性方程组解空 间的一个基 (1)证明51,52，5n线性无关 由于n-r个n-r维向量 00: 线性无关， 所以n-r个n维向量51,52，.，5m-r亦线性无关

下面证明 是齐次线性方程组解空 间的一个基． n r , , ,  1  2   −                                           1 0 0 , , 0 1 0 , 0 0 1     由于 n − r 个 n − r 维向量 线性无关， 所以 n − r 个 n 维向量 n r 亦线性无关. , , ,  1  2   − (1) , , , . 证明 1  2   n 线性无关

(2)证明解空间的任一解都阿由51,52，.，5m- 线性表示 设x=5=(1·2,+1.n)为上述 方程组的一个解.再作5,52，5m,的线性组合， 7=,+151+九+252+.+九n5m-m 由于51,52，5，是Ax=0的解，故7也是4x=0的 解。 下面来证明5=n 回

. (2) , , , 1 2 线性表示 证明解空间的任一解都可 由     n−r ( ) .1 1 方程组的一个解 设 为上述 T x =  =   r r+   n , , , , 再作 1  2   n−r 的线性组合  = r+1 1 + r+2 2 ++  n n−r 由于 是 的解 故 也是 的 解 . n r , , ,  1  2   − Ax = 0 ,  Ax = 0 下面来证明 = 

7=+151+2,+252+.+n5m, _bn -b2 _b b, =九+1 ++2 0 +.+2 0 0 1 .: 0 0 由于与7都是方程Ax=0的解，而Ax=0又等价于

                      − − = + 0 0 1 1 11 1   r r b b                        − − + + 0 1 0 2 12 2   r r b b                        − − + + − − 1 0 0 1    r,n r ,n r n b b   = r+1 1 + r+2 2 ++  n n−r                       = + + n r r r c c      2 1 1 由于与都是方程Ax = 0的解,而Ax = 0又等价于