《线性代数》课程PPT教学课件（同济第五版）第3章 矩阵的初等变换与线性方程组 3.2 初等矩阵

矩阵的和等变换与依促方程组 第四节 初等矩阵 一、初等矩阵的概念 三 初等矩阵的应用 三、小结思考题 带助

一、初等矩阵的概念 矩阵的初等变换是矩阵的一种基本运算，应 用广泛 定义由单位矩阵E经过一次初等变换得到的方 阵称为初等矩阵： 三种初等变换对应着三种初等方阵 1.对调两行或两列； 2.以数k≠0乘某行或某列； 3.以数k乘某行（列）加到另一行（列）上去

定义 由单位矩阵 经过一次初等变换得到的方 阵称为初等矩阵. E 三种初等变换对应着三种初等方阵. 矩阵的初等变换是矩阵的一种基本运算，应 用广泛. 一、初等矩阵的概念       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1

1、对调两行或两列 对调E中第i,j两行，即(，)，得初等方阵 ←第i行 E(i,)= -第j行 上页 回

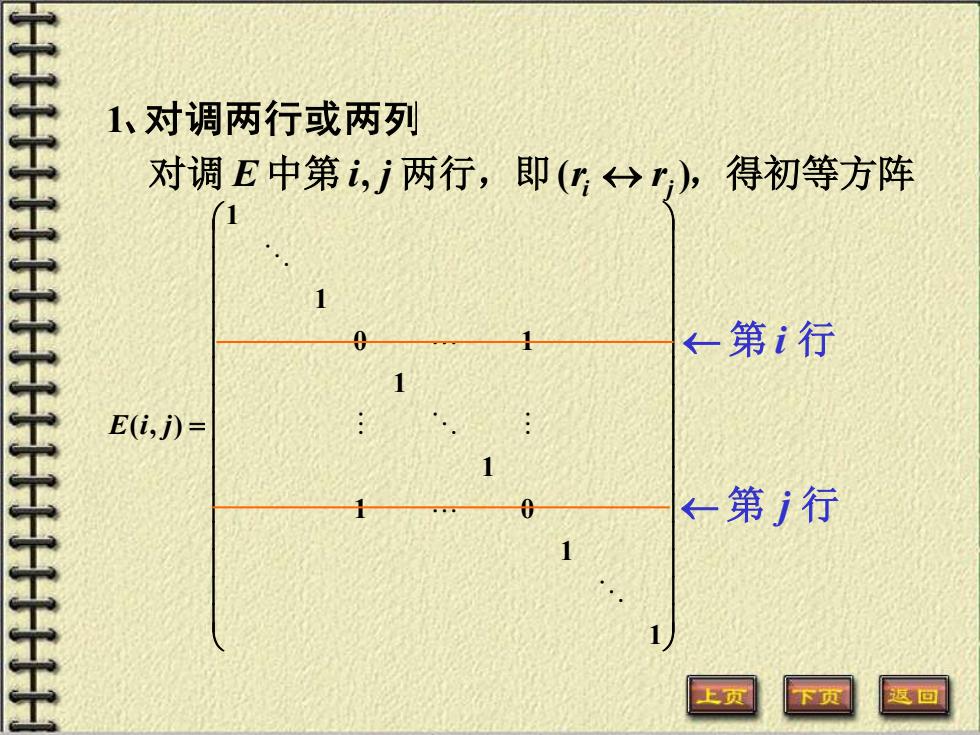
对调 E 中第 i, j 两行，即(ri  rj )，得初等方阵 1、对调两行或两列                                   = 1 1 1 0 1 1 0 1 1 1 ( , )        E i j  第 i 行  第 j 行

用m阶初等矩阵Enm(i,j)左乘A=(a)xn,得 011 12 《第i行 E(i,j)A= m ←-第j行 相当于对矩阵A施行第一种初等行变换： 把A的第i行与第j行对调（→r)

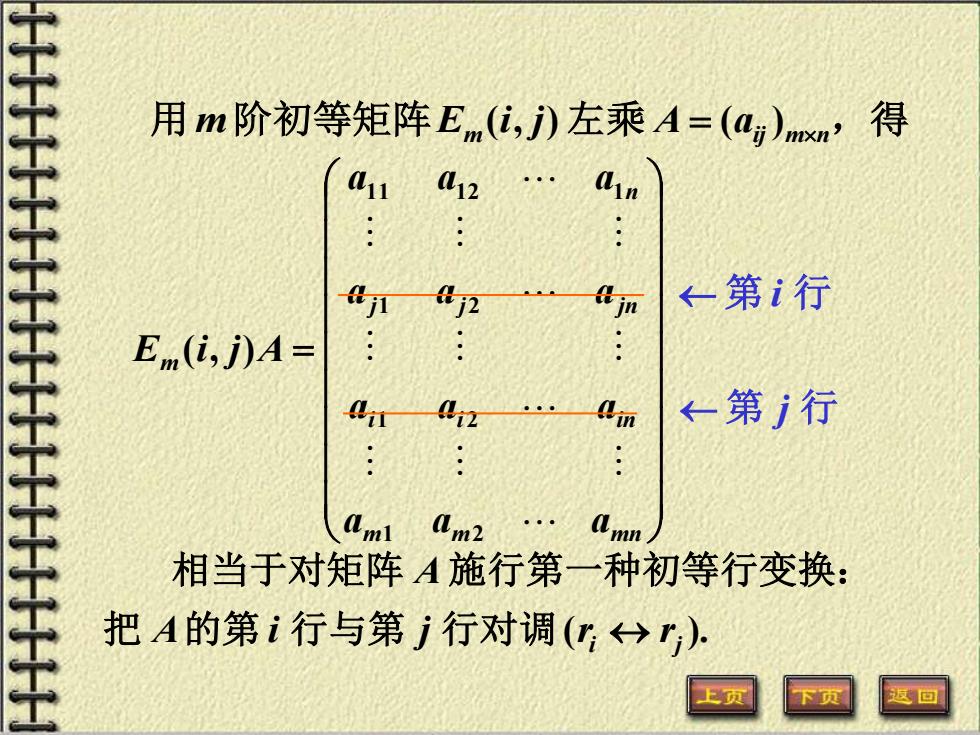
用m 阶初等矩阵Em (i, j) 左乘 A = (aij)mn，得                       = m m mn i i in j j jn n m a a a a a a a a a a a a E i j A              1 2 1 2 1 2 1 1 1 2 1 ( , )  第 i 行  第 j 行 ( ). i j A i j r r A 把 的第 行与第 行对调  相当于对矩阵 施行第一种初等行变换：

类似地， 以n阶初等矩阵En(i,j)右乘矩阵A, 41 41i 21 AE,(i,j)= 相当于对矩阵A施行第一种初等列变换： 把A的第i列与第j列对调(c:)cj) 上页 区回

以 阶初等矩阵 右乘矩阵 ， 类似地， n En (i, j) A               = m mj mi mn j i n j i n n a a a a a a a a a a a a AE i j              1 2 1 2 2 2 1 1 1 1 1 ( , ) ( ). i j A i j c c A 把 的第 列与第 列对调  相当于对矩阵 施行第一种初等列变换：