
《数学建模与数学实验》实验指导书 《数学建模与数学实验》实验指导书 基础实验一:matlab程序设计与作图 实验目的 熟悉MATLAB软件的用户环境:了解MATLAB软件的一般命令:掌握MATLAB向 量、数组、矩阵操作与运算函数:掌握MATLAB软件的基本绘图命令:掌握MATLAB语 言的几种循环、条件和开关选择结构,及其编程规范。 通过该实验的学习,使学生能灵活应用MATLAB软件解决一些荷单问题,能借助 MATLAB软件的绘图功能,对函数的特性进行探讨,广泛联想,大胆猜想,发现进而证实 其中的规律。 实验内容 1.MATLAB软件的数组操作及运算练习: 2.直接使用MATLAB软件进行作图练习: 3.用MATLAB语言编写命令M文件和函数M文件 实验步臻 1.在D盘建立一个自己的文件夹: 2.开启软件平台一MATLAB,将你建立的文件夹加入到MATLAB的搜素路径中: 3.利用帮助了解函数max,min,sum,mean,sort,.length,rand,size和diag的功能和用 法: 4.开启MATLAB编辑窗口,键入你编写的M文件(命令文件或函数文件): 5.保存文件(注意将文件存入你自己的文件夹)并运行: 6.若出现错误,修改、运行直到输出正确结果 7.写出实验报告,并浅谈学习心得体会。 实验要求与任务 根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的一问题一算 法与编程一→计算结果或图形→心得体会) 「3117 「11-1 1.已知矩阵A=212,B=2-10 123 101 第1页
《数学建模与数学实验》实验指导书 第1页 《数学建模与数学实验》实验指导书 基础实验一:matlab 程序设计与作图 实验目的 熟悉 MATLAB 软件的用户环境;了解 MATLAB 软件的一般命令;掌握 MATLAB 向 量、数组、矩阵操作与运算函数;掌握 MATLAB 软件的基本绘图命令;掌握 MATLAB 语 言的几种循环、条件和开关选择结构,及其编程规范。 通过该实验的学习,使学生能灵活应用 MATLAB 软件解决一些简单问题,能借助 MATLAB 软件的绘图功能,对函数的特性进行探讨,广泛联想,大胆猜想,发现进而证实 其中的规律。 实验内容 1.MATLAB 软件的数组操作及运算练习; 2.直接使用 MATLAB 软件进行作图练习; 3.用 MATLAB 语言编写命令 M 文件和函数 M 文件。 实验步骤 1.在 D 盘建立一个自己的文件夹; 2.开启软件平台——MATLAB,将你建立的文件夹加入到 MATLAB 的搜索路径中; 3.利用帮助了解函数 max, min, sum, mean, sort, length,rand, size 和 diag 的功能和用 法; 4.开启 MATLAB 编辑窗口,键入你编写的 M 文件(命令文件或函数文件); 5.保存文件(注意将文件存入你自己的文件夹)并运行; 6.若出现错误,修改、运行直到输出正确结果; 7.写出实验报告,并浅谈学习心得体会。 实验要求与任务 根据实验内容和步骤,完成以下具体实验,要求写出实验报告(实验目的→问题→算 法与编程→计算结果或图形→心得体会) 1. 已知矩阵 = 1 2 3 2 1 2 3 1 1 A , − − = 1 0 1 2 1 0 1 1 1 B

《数学建模与数学实验》实验指导书 要求:(1)屏幕输出A与B:(2)A的转置A:(3)求A+B的值:(4)求A-B的值:(5) 求4A:(6)求A×B:(7)求A. 2.有一函数xy=2+si0+2,写一程序,输入自变量的值,输出函数值。 3.用plot,fplot分别绘制函数=cos(tan(元x》图形 4绘制函数r=a1-sm ly=a(1-cos' 在1e[0,2]上的图形。 5.作出下列曲面的三维图形: x=(1+cosu)cosv, y=(1+cosu)sin v, z=sin u. ue(0,2π,ve(0,2) 6.建立一个M文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其 各位数字的立方和等于该数本身。例如:153是一个水仙花数,因为153=13+53+3。 A=0: a=fix(x/100)b-fix(x-a*100)/10),c=xa*100-b*10 ifx==a^3+b3+c3 A=[A.x] end end disp(A) 基础实验二:matlab函数拟合 实验目的:掌握用matlab进行函数拟合的方法。 实验内容: 根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型 (L0 gistic模型)中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。 表!美国人口统计数据 第2项
《数学建模与数学实验》实验指导书 第2页 要求:(1)屏幕输出 A 与 B;(2)A 的转置 A′;(3)求 A+B 的值;(4)求 A-B 的值;(5) 求 4A;(6)求 A×B;(7)求 A-1. 2. 有一函数 f(x,y)=x 2+sinxy+2y,写一程序,输入自变量的值,输出函数值。 3. 用 plot,fplot 分别绘制函数 y=cos(tan( x))图形。 4. 绘制函数 = − = − (1 cos ) ( sin ) 3 3 y a t x a t t 在 t [0,2 ] 上的图形。 5. 作出下列曲面的三维图形: = = + = + (0,2 ), (0,2 ) sin , (1 cos )sin , (1 cos ) cos , u v z u y u v x u v 6.建立一个 M 文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其 各位数字的立方和等于该数本身。例如:153 是一个水仙花数,因为 153=13+53+33。 A=[]; a=fix(x/100);b=fix((x-a*100)/10);c=x-a*100-b*10; if x==a^3+b^3+c^3 A=[A,x]; end end disp(A) 基础实验二:matlab 函数拟合 实验目的:掌握用 matlab 进行函数拟合的方法。 实验内容: 根据美国人口从 1790 年到 1990 年间的人口数据(如下表),确定人口指数增长模型 (Logistic 模型)中的待定参数,估计出美国 2010 年的人口,同时画出拟合效果的图形。 表 1 美国人口统计数据
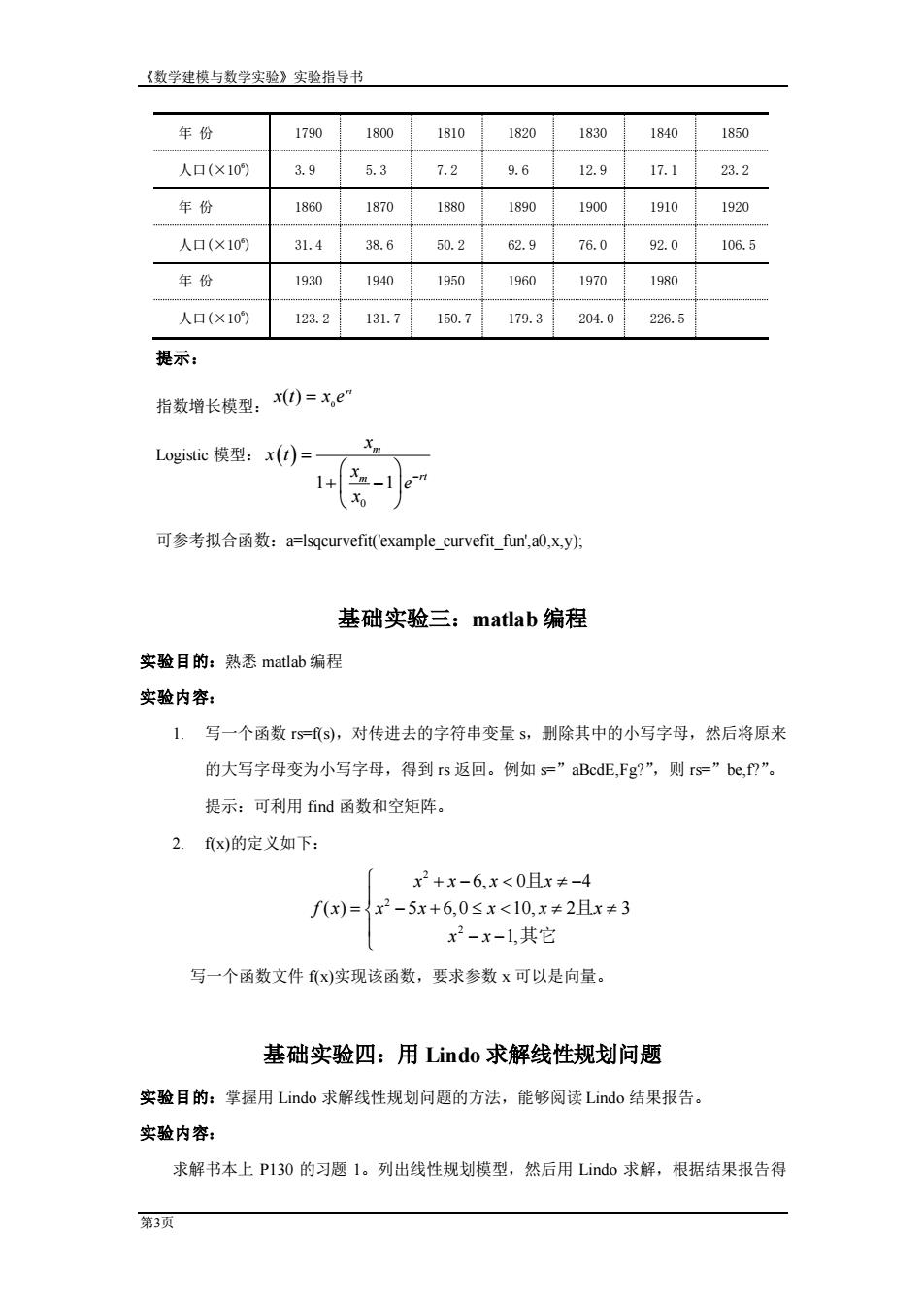
《数学建模与数学实验》实验指导书 年份 1790 1800 1810 1820 1830 1840 1850 人口(×10) 3.9 5.3 7.2 9.6 12.9 17.123.2 年份 1860 1870 1880 1890 1900 1910 1920 人口(×10 31.4 38.6 50.2 62.976.0 92.0 106.5 年份 1930 1940 1950 1960 1970 1980 人口(×10 123.2 131.7 150.7 179.3 204.0 26.5 提示: 指数增长模型:0=x,e Logistic模型:x()= +-le x月 可参考拟合函数:a=-lsqcurvefit(example_curvefit_fun,aO,xy 基础实验三:matlab编程 实验目的:熟悉matlab编程 实验内容: 1.写一个函数SS),对传进去的字符串变量s,删除其中的小写字母,然后将原来 的大写字母变为小写字母,得到rs返回。例如s=”aBcd正,Fg?”,则rs”be,f?”。 提示:可利用find函数和空矩阵。 2.fx)的定义如下: x2+x-6,x<0且x≠-4 f(x)={x2-5x+6,0≤x<10,x≠2且x≠3 x2-x-1其它 写一个函数文件x实现该函数,要求参数x可以是向量。 基础实验四:用Lindo求解线性规划问题 实验目的:掌握用Lindo求解线性规划问题的方法,能够阅读Lindo结果报告。 实验内容: 求解书本上PI30的习题l。列出线性规划模型,然后用Lido求解,根据结果报告得 第3项
《数学建模与数学实验》实验指导书 第3页 年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106 ) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106 ) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106 ) 123.2 131.7 150.7 179.3 204.0 226.5 提示: 指数增长模型: rt x t x e0 ( ) = Logistic 模型: ( ) 0 1 1 m m rt x x t x e x − = + − 可参考拟合函数:a=lsqcurvefit('example_curvefit_fun',a0,x,y); 基础实验三:matlab 编程 实验目的:熟悉 matlab 编程 实验内容: 1. 写一个函数 rs=f(s),对传进去的字符串变量 s,删除其中的小写字母,然后将原来 的大写字母变为小写字母,得到 rs 返回。例如 s=”aBcdE,Fg?”,则 rs=”be,f?”。 提示:可利用 find 函数和空矩阵。 2. f(x)的定义如下: 2 2 2 6, 0 4 ( ) 5 6,0 10, 2 3 1, x x x x f x x x x x x x x + − − = − + − − 且 且 其它 写一个函数文件 f(x)实现该函数,要求参数 x 可以是向量。 基础实验四:用 Lindo 求解线性规划问题 实验目的:掌握用 Lindo 求解线性规划问题的方法,能够阅读 Lindo 结果报告。 实验内容: 求解书本上 P130 的习题 1。列出线性规划模型,然后用 Lindo 求解,根据结果报告得

《数学建模与数学实验》实验指导书 出解决方案。 提示: 模型可以如下建立: 设投资证券A,B,C,D,E的金额分别为x1,x2,x3,x4x5万元 max0.043x1+0.027x2+0.025x3+0.022x4+0.045x5 x2+x3+X4>=400 x1+x2+x3+x4+x5<=1000 (2x1+2x2+x3+x4+5x5)/x1+x2+x3+x4+x5)<=1.4 (9x1+15x2+4x3+3x4+2x5)/x1+x2+x3+x4+x5)<=5 使用Lindo的一些注意事项 1. “>”与“=”功能相同 2.变量与系数间可有空格(甚至回车),但无运算符 3.变量以字母开头,不能超过8个字符 4.变量名不区分大小写(包括关健字) 5.目标函数所在行是第一行,第二行起为约束条件 6.行号自动产生或人为定义,以“)”结束 7.“1”后为注释。 8.在模型任何地方都可以用“TTE”对模型命名 9.变量不能出现在一个约束条件的右端 10.表达式中不接受括号和逗号等符号 .表达式应化简,如2x1+3x2-4x1应写成-2x1+3x2 l2.缺省假定所有变量非负,可在模型“END”语句后用“FREE name'”将变量name的非 负假定取消 13.可在“END”后用“SUB”或“SLB”设定变量上下界。例如:“bx110”表示“x1<10” 14.“END”后对O-l变量说明:INTn或INT name 15.“END”后对整数变量说明:GINn或GIN name 基础实验五:用Lingo求解非线性规划问题 实验目的:掌握用Ligo求解非线性规划问题的方法。 第4页
《数学建模与数学实验》实验指导书 第4页 出解决方案。 提示: 模型可以如下建立: 设投资证券 A,B,C,D,E 的金额分别为 x1,x2,x3,x4,x5 万元. max 0.043x1+0.027x2+0.025x3+0.022x4+0.045x5 x2+x3+x4>=400 x1+x2+x3+x4+x5<=1000 (2x1+2x2+x3+x4+5x5)/(x1+x2+x3+x4+x5)<=1.4 (9x1+15x2+4x3+3x4+2x5)/(x1+x2+x3+x4+x5)<=5 使用 Lindo 的一些注意事项 1. “>”与“>=”功能相同 2. 变量与系数间可有空格(甚至回车),但无运算符 3. 变量以字母开头,不能超过 8 个字符 4. 变量名不区分大小写(包括关键字) 5. 目标函数所在行是第一行,第二行起为约束条件 6. 行号自动产生或人为定义,以“)”结束 7. “!”后为注释。 8. 在模型任何地方都可以用“TITLE”对模型命名 9. 变量不能出现在一个约束条件的右端 10. 表达式中不接受括号和逗号等符号 11. 表达式应化简,如 2x1+3x2-4x1 应写成-2x1+3x2 12. 缺省假定所有变量非负,可在模型“END”语句后用“FREE name”将变量 name 的非 负假定取消 13. 可在“END”后用“SUB”或“SLB”设定变量上下界。例如:“sub x1 10”表示“x1<=10” 14. “END”后对 0-1 变量说明:INT n 或 INT name 15. “END”后对整数变量说明:GIN n 或 GIN name 基础实验五:用 Lingo 求解非线性规划问题 实验目的:掌握用 Lingo 求解非线性规划问题的方法

《数学建模与数学实验》实验指导书 实验内容: 求解书本上P132的习题7。列出非线性规划模型,然后用Lig0求解,根据结果报告 得出解决方案。 提示 可参考书上钢管切割模型的例子,注意有所修改。比如目标函数应该为: m1n=(x1+0.1)*y1+(x2+0.2)*y2+(x3+0.3)*y3+(x4+0.4)*y4; y1,y2,y3,y4是0-1变量。 约束条件可为: x1*r11+x2*r12+x3*r13+x4*r14>=15;。·。 290*r11+315*x21+350*r31+455*r41<-y1*1850;··。 r11+x21+r31+r41<=y1*5。 x1*y1+x2*y2+x3*y3+x4*y4<=22 x1*y1+x2*y2+x3*y3+g4*y4>-19: x1<-y1*100:·。· 基础实验六:用Lingo求解大规模线性规划问题 实验目的:掌握用Ligo求解大规模线性规划问题的方法。 实验内容: 求解全国大学生数学建模竞赛O5年B题问题2:DVD的分配。会员每次租赁3张DVD,现 在给出网站手上的100种DVD的现有张数和当前需要处理的1000位会员的在线订单,如何对 这些DVD进行分配,才能使会员获得最大的满意度? 现有DVD张数和当前需要处理的会员的在线订单(表格格式示例 DVD编号 D001 D002 D003 D004 DVD现有数量 10 40 15 20 C0001 会员 C0002 0 在线 C0003 钉单 C0004 第5页
《数学建模与数学实验》实验指导书 第5页 实验内容: 求解书本上 P132 的习题 7。列出非线性规划模型,然后用 Lingo 求解,根据结果报告 得出解决方案。 提示: 可参考书上钢管切割模型的例子,注意有所修改。比如目标函数应该为: min =(x1+0.1)*y1+(x2+0.2)*y2+(x3+0.3)*y3+(x4+0.4)*y4; y1,y2,y3,y4是0-1变量。 约束条件可为: x1*r11+x2*r12+x3*r13+x4*r14>=15; 。 290*r11+315*r21+350*r31+455*r41<=y1*1850; 。 r11+r21+r31+r41<=y1*5; 。 x1*y1+x2*y2+x3*y3+x4*y4<=22; x1*y1+x2*y2+x3*y3+x4*y4>=19; x1<=y1*100; 。 基础实验六:用 Lingo 求解大规模线性规划问题 实验目的:掌握用 Lingo 求解大规模线性规划问题的方法。 实验内容: 求解全国大学生数学建模竞赛05年B题问题2:DVD的分配。会员每次租赁3张DVD,现 在给出网站手上的100种DVD的现有张数和当前需要处理的1000位会员的在线订单,如何对 这些DVD进行分配,才能使会员获得最大的满意度? 现有 DVD 张数和当前需要处理的会员的在线订单(表格格式示例) DVD 编号 D001 D002 D003 D004 . DVD 现有数量 10 40 15 20 . 会员 在线 订单 C0001 6 0 0 0 . C0002 0 0 0 0 . C0003 0 0 0 3 . C0004 0 0 0 0 . . . . . .