
第华章 导数与微分 高等数学少学时 例4变速直线运动的瞬时速度. 设某一物体作变速直线运动,在0,内走过的路程为s),物 体从t运动到。+△r0<t,t。+△t<t)的平均速度为 D=S(,+△)-s)△s △t △t 时间间隔越短,平均速度y越接近物体在时刻的瞬时速度,当 △t0时,如果上式的极限存在,则该极限为函数在时刻的瞬 时速度,记为 y lim s(t+△t)-s(to) △t→0 △t 也称v是函数s()在点的变化率. 北京邮电大学出版社 6
6 t 0运动到t 0 + t(0 t 0 ,t 0 + t t)的平均速度为 . ( ) ( ) 0 0 t s t s t t s t v = + − = . ( ) ( ) lim 0 0 0 t s t t s t v t + − = → 变速直线运动的瞬时速度. 体从 Δt→0时,如果上式的极限存在,则该极限为函数在时刻 t0的瞬 时速度,记为 也称v是函数s (t)在t0点的变化率. 例4 设某一物体作变速直线运动,在[0, t]内走过的路程为s (t),物 时间间隔越短,平均速度 越接近物体在t v 0时刻的瞬时速度,当
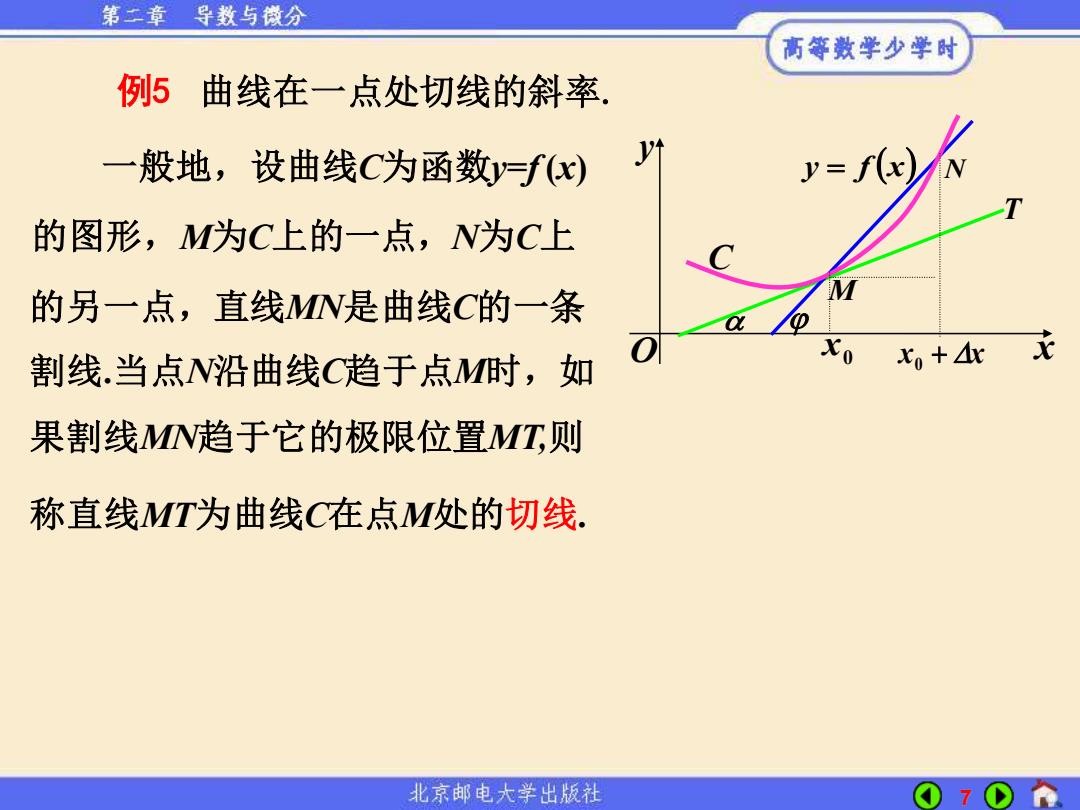
第华章 导数与微分 高等数学少学时 例5曲线在一点处切线的斜率. 一般地,设曲线C为函数y=f(x) y 的图形,M为C上的一点,N为C上 的另一点,直线MN是曲线C的一条 割线.当点W沿曲线C趋于点M时,如 0x+衣 果割线MN趋于它的极限位置MT,则 称直线MT为曲线C在点M处的切线. 北京邮电大学出版社 07
7 例5 曲线在一点处切线的斜率. 一般地,设曲线C为函数y=f (x) 的另一点,直线MN是曲线C的一条 O x y M N T x + x 0 x0 y = f (x) C 的图形,M为C上的一点,N为C上 割线.当点N沿曲线C趋于点M时,如 果割线MN趋于它的极限位置MT,则 称直线MT为曲线C在点M处的切线

第章 导数与微分 高等数学少学时 设M,N的坐标分别为(x,f(x)(x+△x,f(x+△),割线 MN的倾角为p,则割线的斜率为 f(x+△x)-f(x) △x 当点N沿曲线C趋于点M时(此时△x→0),如果上式的极限存 在,记为k,即 k=lim f(x,+△x)-f(xo) △x→0 △x 则极限值k就是切线MT的斜率这里=tana,a为切线MT的倾角.k 是函数y=f(x)在x处的变化率 北京邮电大学出版社
8 ( , ( )),( , ( )), 设M,N的坐标分别为 x0 f x0 x0 + x f x0 + x MN的倾角为φ,则割线的斜率为 割线 . ( ) ( ) tan 0 0 x f x x f x + − = 当点N沿曲线C趋于点M时(此时Δx→0),如果上式的极限存 在,记为k,即 , ( ) ( ) lim 0 0 0 x f x x f x k x + − = → 则极限值k就是切线MT的斜率.这里k= tanα, α为切线MT的倾角.k 是 函数y=f (x)在x0处的变化率