
(1)-(2): 2y2(x)-2x4-x2+y(x)=0 即 (y(x)-x2)2y(x)+2x2+1)=0,由此得y(x)=x2或 )=-x2-】,把)=x代入①和2)满足方程, 2 而y=-x2-】不满足方程(1)和(2,故公共解为=x2 3.求微分方程y+y2-y=0的直线积分曲线。 解:设y=心+b(其中,b为常数)为所给方程的解 将y及y'=a代入所给方程得 而 返回 结束
首页 上页 返回 下页 结束 铃 2 4 2 2 ( ) 2 ( ) 0 y x x x y x − − + = 2 2 ( ( ) - )(2 ( ) 2 1) 0 y x x y x x + + = , 2 由此得 y x x ( ) = 或 2 2 1 ( ) , ( ) 1 2 2 y x x y x x = − − = 把 代入 ( ) 和 ( ) 满足方程, 2 2 1 (2) 2 而y x y x = − − = 不满足方程(1)和 ,故公共解为 设y ax b a b = + (其中 , 为常数)为所给方程的解 即 (1) (2) : − 2 3. 求微分方程 y xy y + = - 0的 直线积 分 曲 线。 解: 将 y y a 及 = 代入所给方程得

a"x=ax-a+b (2) 比较(2)两端同次幂的系数,得 解:a=0b=0或a=1b=1 故所求直线方程为y=0或y=x+1 3.试建立分别具有下列性质的曲线所满足的微分方程: (1)曲线上任一点的切线与该点的向径夹角为. 解:设所求曲线方程为=y(x),过其上任一点 M(x,y)作切线MT及向径OM如图,则显然o=p-O 首页 上页 返回 下页 结束 铃
首页 上页 返回 下页 结束 铃 故所求直线方程为 y y x = = + 0 1 或 (1)曲线上任一点的切线与该点的向径夹角为. M x y MT OM ( , ) - 作切线 及向径 如图,则显然 = 设所求曲线方程为y y x = ( ),过其上任一点 2 a x ax a b = − + (2) 比较(2)两端同次幂的系数,得 a b a b = = = = 0 0 1 1 或 2 0 a a b a = − = , 3.试建立分别具有下列性质的曲线所满足的微分方程 : 解: 解:
记k=tanc=tanx(p-B), 则 k=_ anθ-tanp (1) 1+tan0.tan tan6=X,anp=光 M(,y) 代入(1)得 0 y'. tana= x=xy'-y 1+. x+y 首而 返回 下 结束 铃
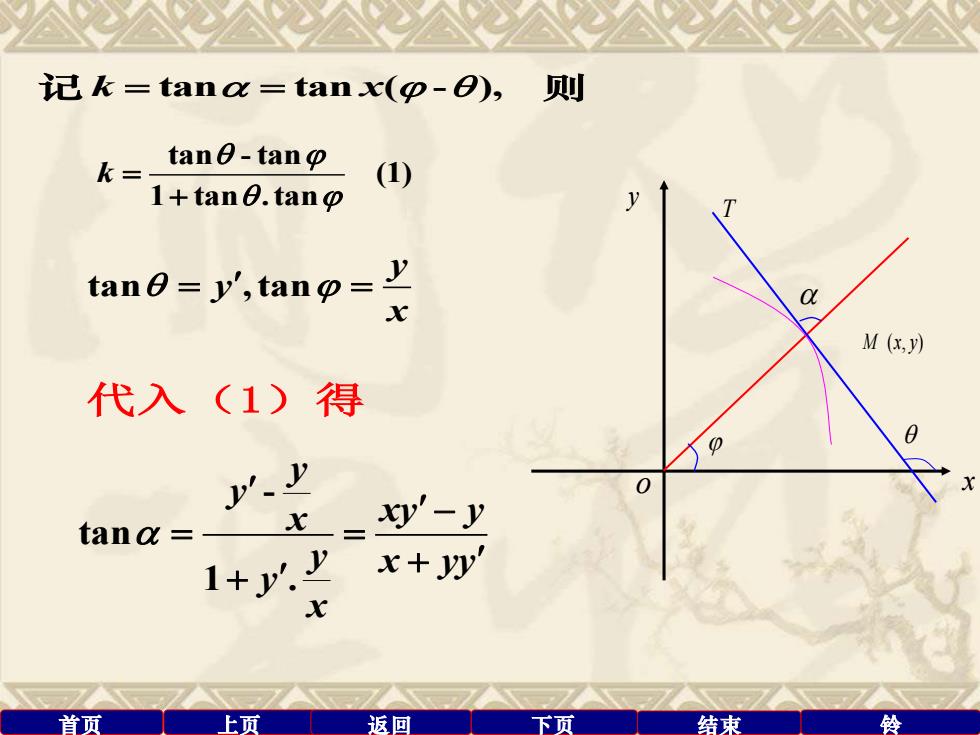
首页 上页 返回 下页 结束 铃 记 k x = = tan tan ( - ), 则 tan - tan (1) 1 tan . tan k = + tan , tan y y x = = - tan 1 . y y x xy y y x yy y x − = = + + 代入(1)得 M x y ( , ) T x y o

从而,我们得到所求曲线所满足的微分方程: y'=y+ 5.求微分方程的通解。 x-ky 东-(c+n+++8*1 (1) 解:将上试写成: 少=x2+2x+16y2+8y+8y+3 =(x+4y)+2(x+4y)+3(2) 令x+4y=w,则少=(血-1),代入2)整理得 dx 4 dx =42+8u+13 (3 dx 首页 上页 返回 下页 结束
首页 上页 返回 下页 结束 铃 从而,我们得到所求曲线所满足的微分方程: 5.求微分方程的通解 . 将上试写成: 2 2 2 16 8 8 3 dy x x y y xy dx = + + + + + ( ) ( ) 2 = + + + + x y x y 4 2 4 3 (2) 1 ( 4 2) dy du dx dx 则 = ( -1),代入 整理得 2 4 8 13 (3) du u u dx = + + ( ) ( ) 2 2 1 4 1 8 1 dy x y xy dx = + + + + + (1) - y kx y x ky + = 令x y u + = 4 , 解:

分离变量积分」 du =x+C 4u2+8u+13 du 2(u+1) -arctan 3 arctan 2u+0=6x+6c, 回到(x,y)变量, 整理 3 得(1)的通解为 tan(6x+c)=子(c+4y+1) 其中c为任意常数, 6.求解微分方程 少_y-2x2 (1) dx 2.9y5+x2y2 而 而 返回 结束
首页 上页 返回 下页 结束 铃 2 4 8 13 du x c u u = + + + 分离变量积分: 2 2 2 1 1 1 2( 1) arctan 4 8 13 4 6 3 3 ( 1) ( ) 2 du u du u u u + = = + + + + 2( 1) arctan 6 6 3 u x c + = + , ( ) ( ) 2 tan 6 4 1 3 x c x y + = + + 其中c为任意常数. 6.求解微分方程 6 2 5 2 2 2 (1) 2 dy y x dx xy x y − = + 回到(x y, )变量,整理 得(1)的通解为