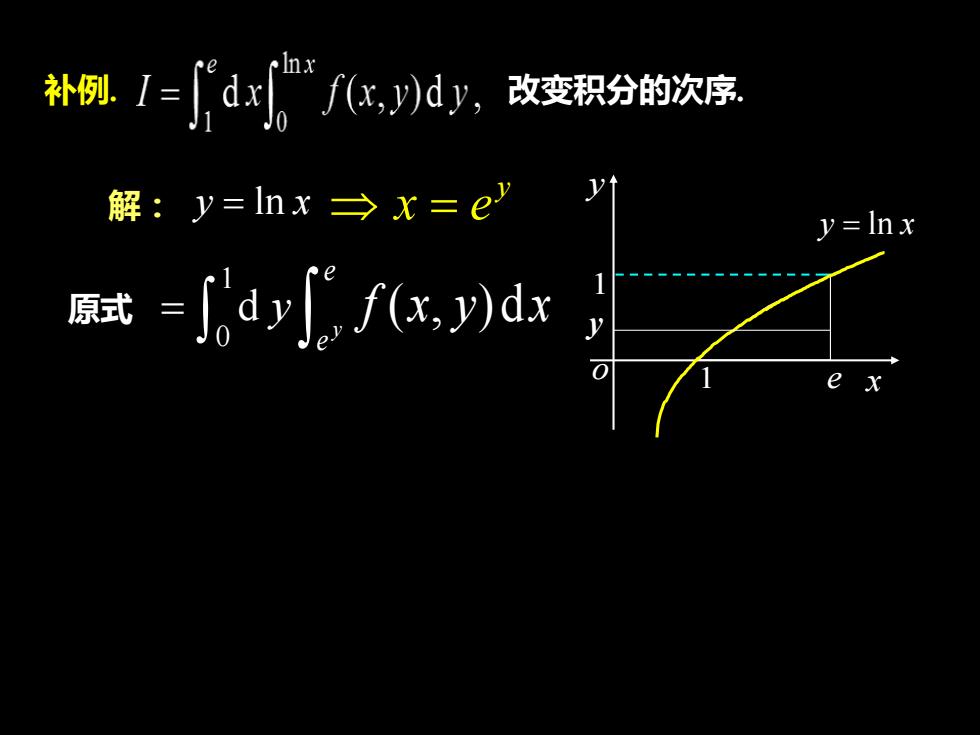
补例. I={~dx""f(x,y)dy,改变积分的次序.yt解: y=lnx=x=ejy= lnxf(x,y)dxdy原式VO
解: y x = ln 原式 补例. 改变积分的次序. 1 0 = d y y = x e 1 y o 1 e x y x = ln y e e y f (x, y) dx

例5.交换下列积分次序?2V28I = [,dx[2 f(x, y)dy+dxf(x, y)dy解:积分域由两部分组成J0≤y≤/8-x20≤V6DD22------.2≤x≤2~/20≤x≤2VExDD将D=Di+D2视为Y-型区域,则022/2 x[ /2y≤x≤/8- y20≤y≤2I = [f,f(x,y)dxdy= Jf(x, y)dxdy自灵返回结束机动-质
例5. 交换下列积分次序 − = + 2 2 8 0 2 2 2 2 0 2 0 d ( , )d d ( , )d x x I x f x y y x f x y y 解: 积分域由两部分组成: , 0 2 0 : 2 2 1 1 x y x D 8 2 2 x + y = D2 2 2 y o 2 x D1 2 2 1 y = x 2 − 2 2 2 0 8 : 2 2 x y x D 将 D = D1 + D2 D : 视为Y–型区域 , 则 2 2y x 8 − y 0 y 2 = D I f (x, y)d x d y − 2 8 2 ( , )d y y f x y x = 2 0 dy 机动 目录 上页 下页 返回 结束