
第六章定积分及其应用 6.1定积分的概念及性质 6.2定积分的计算方法 6.3非正常积分 6.4定积分的应用
第六章 定积分及其应用 6.1 定积分的概念及性质 6.2 定积分的计算方法 6.3 非正常积分 6.4 定积分的应用

6.2定积分的计算方法 回顾:定积分的概念 ∫2fx)dx=im∑f5)△x,· d→0 i=1 ·用定积分的定义直接去求积分和的极限是十分困难的。 。 不定积分和定积分是两个完全干的概念,但是牛顿和 莱布尼茨发现这两个不同概念之间存在着深刻的内在 联系,即所谓的微积分基本定理, ·由此开辟的求定积分的新途径一牛顿莱布尼茨公式, 使积分学和微分学一起构成变量数学的基础学科一一 微积分学
6.2 定积分的计算方法 ⚫ 用定积分的定义直接去求积分和的极限是十分困难的。 ⚫ 不定积分和定积分是两个完全干的概念,但是牛顿和 莱布尼茨发现这两个不同概念之间存在着深刻的内在 联系,即所谓的微积分基本定理, ⚫ 由此开辟的求定积分的新途径——牛顿-莱布尼茨公式, 使积分学和微分学一起构成变量数学的基础学科—— 微积分学. 回顾:定积分的概念 ( ) d lim ( ) . 1 0 = → = n i i i d b a f x x f ξ x
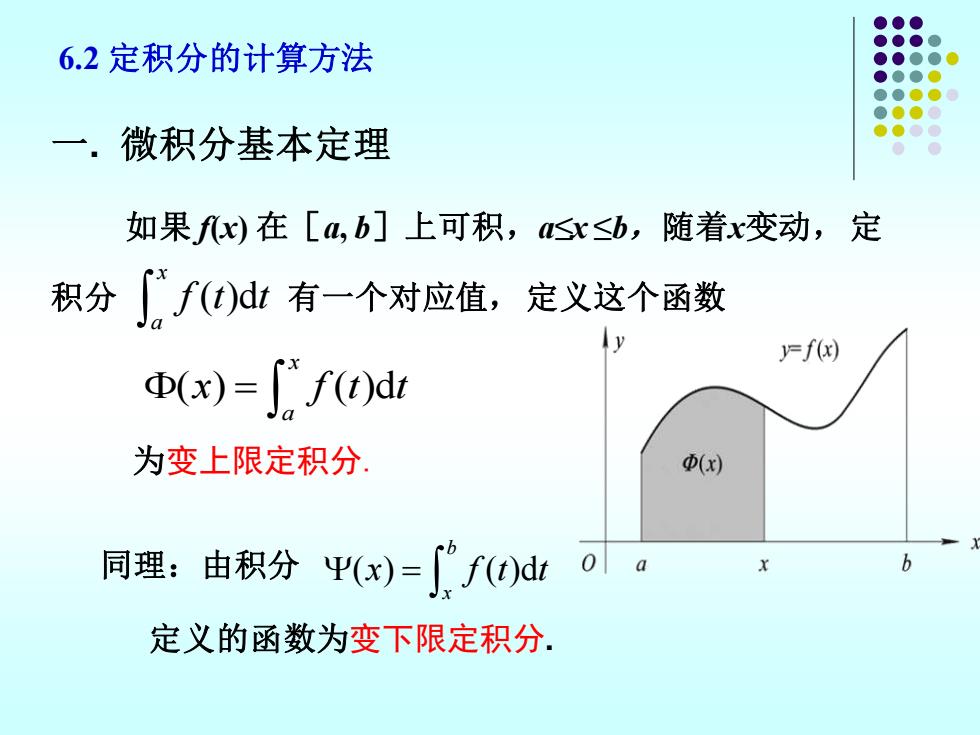
6.2定积分的计算方法 一.微积分基本定理 如果fx)在[4,b]上可积,sx≤b,随着x变动,定 积分f()dt有一个对应值,定义这个函数 Ff树 (x)=["f()di 为变上限定积分 (x) 同理:由积分平(x)=心f)dtoa b 定义的函数为变下限定积分:
6.2 定积分的计算方法 一. 微积分基本定理 如果 f(x) 在[a, b]上可积,a≤x ≤b,随着x变动,定 积分 ( )d 有一个对应值,定义这个函数 x a f t t ( ) ( )d x a = x f t t 为变上限定积分. ( ) ( )d b x = x f t t 同理:由积分 定义的函数为变下限定积分

6.2定积分的计算方法 定理1如果fx)在[a,b]上连续,则变上限积分函数 Φ(x)=fu 在[a,1]上可导,且D'(x)=f(x)(a≤≤b) 即Φ(x)是被积函数f(x)在a,b]上的一个原函数,并且 ①D(x)在[a,b]上连续
6.2 定积分的计算方法 定理 1 如果f(x)在[a, b]上连续,则变上限积分函数 x f t t x a ( ) ( )d = 在 [a, b] 上可导,且 = ( ) ( ) x f x (a≤x≤b) ( ) ( ) [ , ] ( ) [ , ] . x f x a b x a b 即 是被积函数 在 上的一个原函数,并且 在 上连续

6.2定积分的计算方法 Φ'(x)=f(x) 定理1的证明 证 这里要求Φx)的导数,我们就按照导数的定义来求 解.(x)在x+x处的函数值为 (x+Ax)=f(Xlr 由此得函数的增量 △D=Φ(x+Ax)-Φ(x)=fuh-fud -f+f-ffd =∫“f0)d
6.2 定积分的计算方法 证 这里要求Φ(x)的导数,我们就按照导数的定义来求 解. Φ(x)在x+Δx处的函数值为 Φ x x f t t x x a ( ) ( )d + + = 由此得函数的增量 = ( ) ( ) x f x 定理1的证明 = (x + x) −(x) f t dt f t dt x a x x a = − + ( ) ( ) f t dt f t dt f t dt x a x x x x a = + − + ( ) ( ) ( ) ( ) x x x f t dt + =