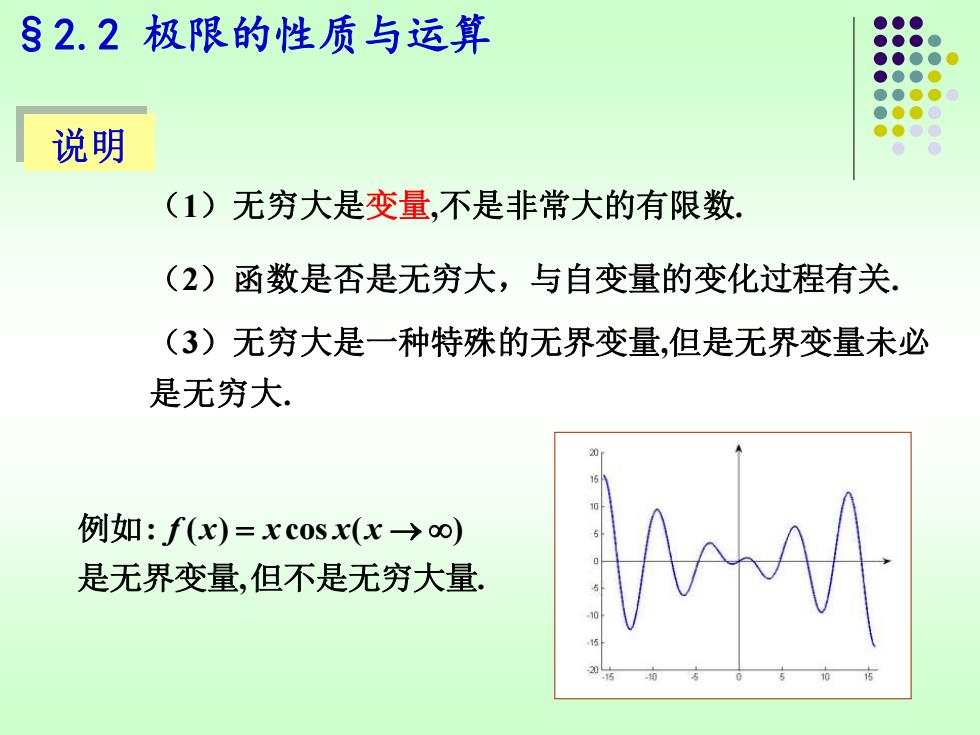
§2.2极限的性质与运算 说明 (1)无穷大是变量,不是非常大的有限数 (2)1 函数是否是无穷大,与自变量的变化过程有关 (3)无穷大是一种特殊的无界变量,但是无界变量未必 是无穷大 例如:f(x)=xc0sx(x→∞) 是无界变量,但不是无穷大量
§2.2 极限的性质与运算 说明 (1)无穷大是变量,不是非常大的有限数. (3)无穷大是一种特殊的无界变量,但是无界变量未必 是无穷大. : ( ) cos ( ) , . 例如 f x x x x = → 是无界变量 但不是无穷大量 (2)函数是否是无穷大,与自变量的变化过程有关
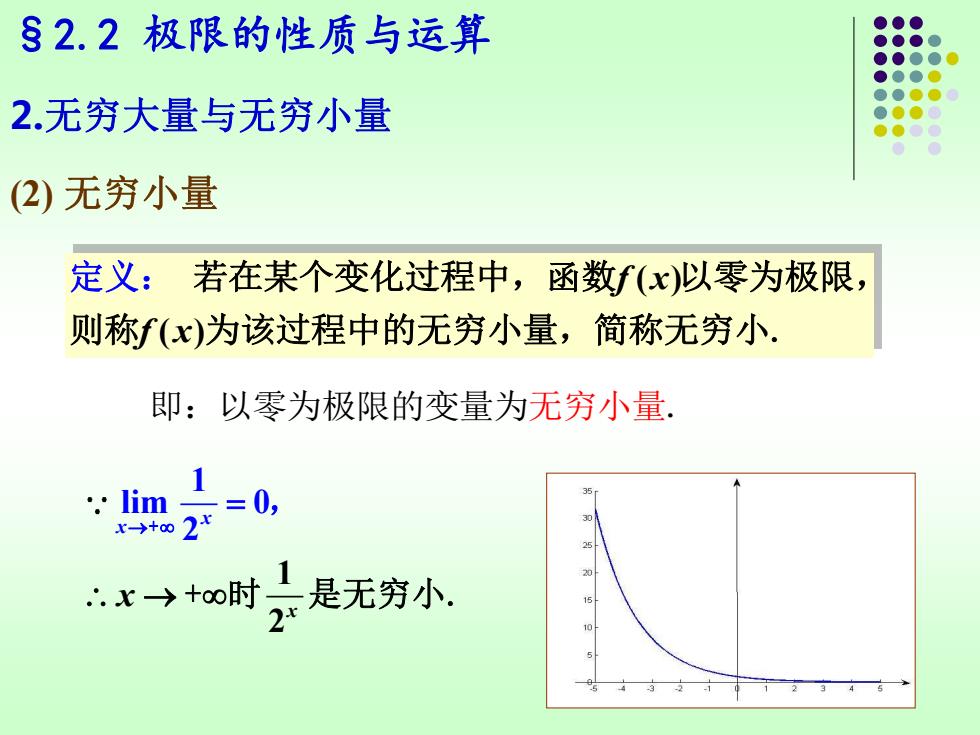
§2.2极限的性质与运算 2.无穷大量与无穷小量 (2)无穷小量 定义:若在某个变化过程中,函数f(x)以零为极限, 则称f(x)为该过程中的无穷小量,简称无穷小. 即:以零为极限的变量为无穷小量, .lim=0, x→+o时是无穷小. 2 345
§2.2 极限的性质与运算 ( ) ( ) f x f x 若在某个变化过程中,函数 以零为极限, 则称 为该过程中的无穷小量,简称 定义: 无穷小. 即:以零为极限的变量为无穷小量. 2.无穷大量与无穷小量 (2) 无穷小量 1 lim 0 1 2 2 x x x x → = → + , + 时 是无穷小

§2.2极限的性质与运算 limsinx=0,∴.当x→0时,函数sinx是无穷小. x->0 ".lim二=0, x-→0X 函数二是当x→o时的无穷小. X 注:数列作为函数的特例,也有无穷大和无穷小. 例如n→o时,2n是无穷大,是无穷小 lim-=0 n-→on
§2.2 极限的性质与运算 0 limsin 0, x x → = → 当x x 0 sin 时,函数 是无穷小. 1 lim 0, x→ x = 1 x x → 函数 是当 时的无穷小. x y 1 = o x y x y 1 = 1 n n2 . n → 数列作为函数的特例,也有无穷大和无穷小. 例如 时, 是无穷大, 注 是无穷小 : 1 lim 0 n→ n =