第六章定积分及其应用 6.1定积分的概念及性质 6.2定积分的计算方法 6.3非正常积分 6.4定积分的应用
第六章 定积分及其应用 6.1 定积分的概念及性质 6.2 定积分的计算方法 6.3 非正常积分 6.4 定积分的应用
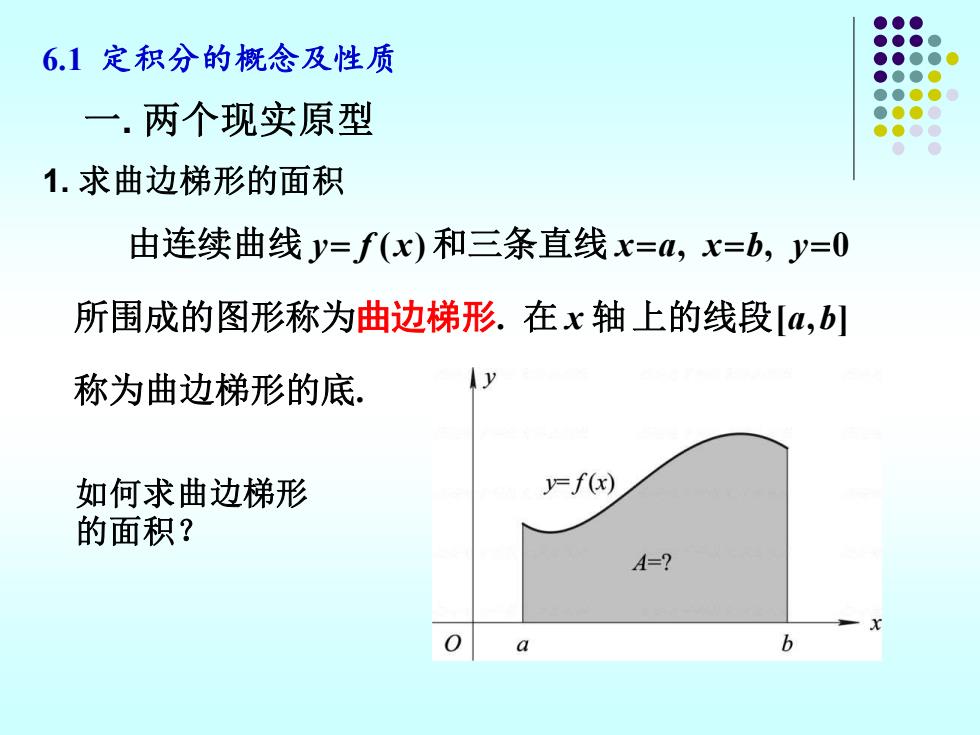
6.1定积分的概念及性质 一.两个现实原型 1.求曲边梯形的面积 由连续曲线y=f(x)和三条直线x=M,x=b,y=0 所围成的图形称为曲边梯形.在x轴上的线段[,b 称为曲边梯形的底。 如何求曲边梯形 y=f(x) 的面积? A=? 0 b
6.1 定积分的概念及性质 由连续曲线 y= f ( x)和三条直线 x=a, x=b, y=0 所围成的图形称为曲边梯形. 在 x 轴上的线段[a,b] 称为曲边梯形的底. 一. 两个现实原型 1. 求曲边梯形的面积 如何求曲边梯形 的面积?
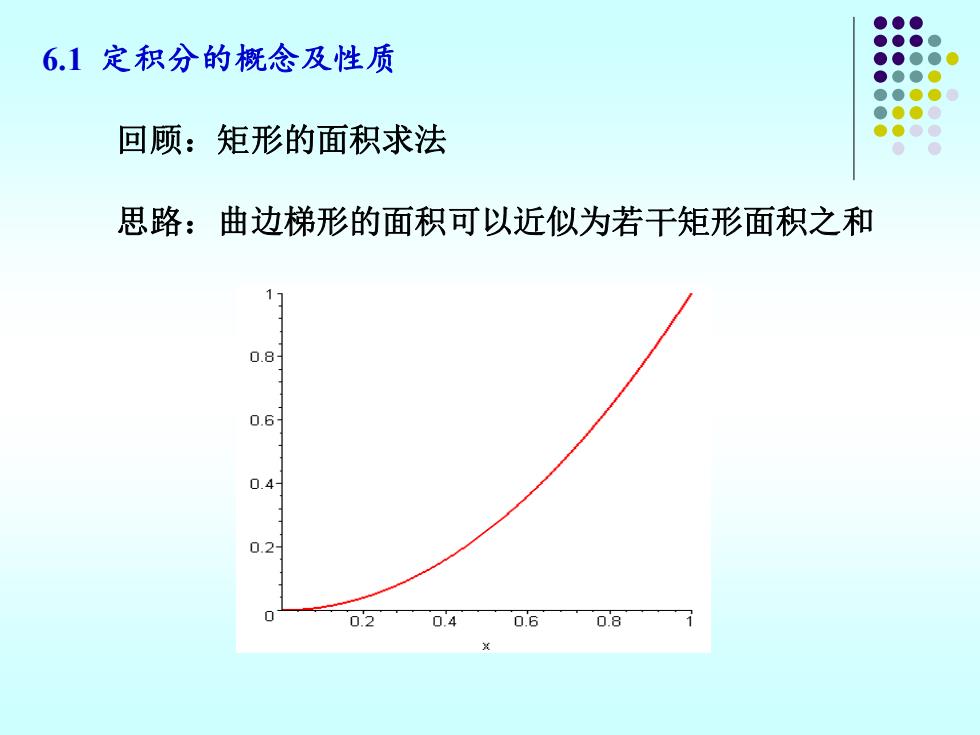
6.1定积分的概念及性质 回顾:矩形的面积求法 思路:曲边梯形的面积可以近似为若干矩形面积之和 0.8 0.6 0.4 0.2 0.2 04 0.6 0.8
6.1 定积分的概念及性质 回顾:矩形的面积求法 思路:曲边梯形的面积可以近似为若干矩形面积之和

6.1定积分的概念及性质 设y=f(x)在[a,b]上连续,且f(x)≥0,求以曲线88 y=f(x)为曲边,底为[a,b]的曲边梯形的面积A. (1)划分 任取分点:a=x0<1<x2<<x-1<x<<x-<Xn=b, 把区间[a,b]分为n个小区间:[i-1,xi(i=1,2,n), [xi-1,xi]的长度记为△xi=xi-xi-1(i=1,2,.,n)为 直线x=xi(i=1,2,.,n-1),把整个曲边梯形 分成个小曲边梯形,其中第i个小曲边梯形的面 积记为△4i(i=1,2,n)
6.1 定积分的概念及性质 设 y= f ( x)在[a,b]上连续,且 f ( x)0,求以曲线 y= f ( x)为曲边,底为[a,b]的曲边梯形的面积 A . 任取分点:a x x x x x x x b = 0 1 2 i−1 i n−1 n = , 把区间[a,b] 分为n个 小区间:[ , ]( 1, 2, , ), xi−1 xi i= n [ , ] ( 1, 2, , ), xi −1 xi 的长度记为xi = xi − xi −1 i = n 直线 x = xi ( i=1, 2, , n−1 ) ,把整个曲边梯形 分成n个 小曲边梯形,其中第 i 个 小曲边梯形的面 积记为 A ( i 1, 2, , n ) i = . (1)划分
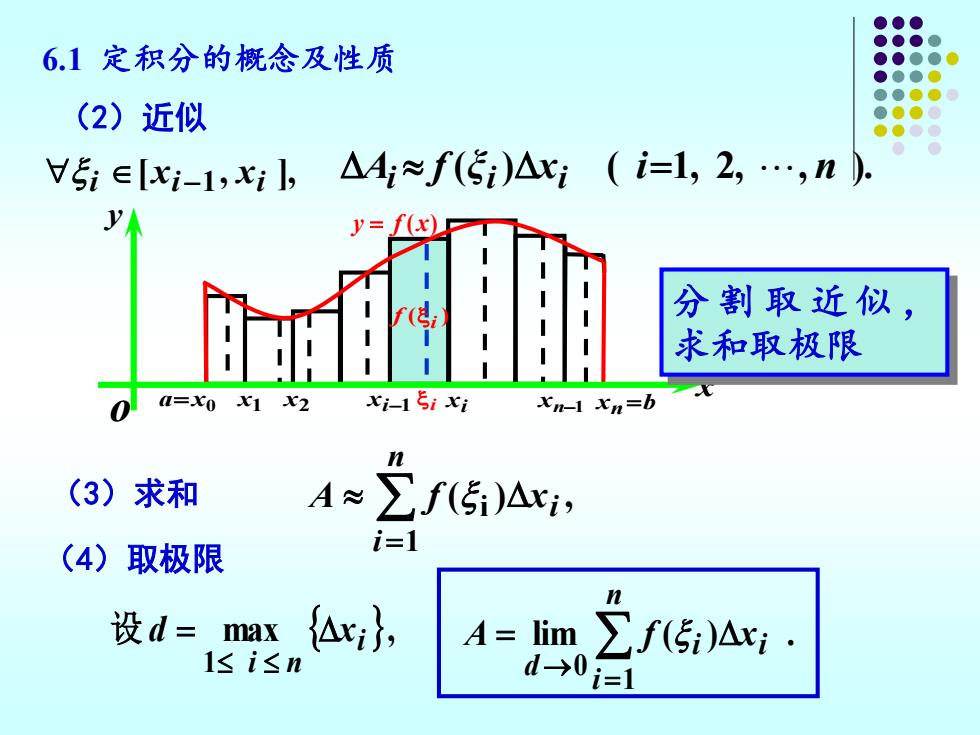
6.1定积分的概念及性质 (2)近似 V5i∈xi-1,x,△4;≈f(5i)△xi(i=l,2,.,n). y=(x) 分割取近似, 求和取极限 Q=X0 X1 x2 xi-1ξixi Xn-1 xn=b (3)求和 A≈∑f(5i)Axi, (4)取极限 i=1 设d= max x}, 4=lim ∑f5)△x lsi≤n d→ i=1
6.1 定积分的概念及性质 [ , ], i xi −1 xi A f (ξ ) x ( i 1, 2, , n ). i i i = (3)求和 (2)近似 lim ( ) . 1 0 → = = n i i i d A f x (4)取极限 max , 1 i i n d = x 设 ( ) , 1 i = n i i A f x i ( )i f o a= x0 x1 x2 xi−1 xi xn−1 xn =b y x y = f (x) 分 割 取 近 似 , 求和取极限