
若x =a,取△r>0,则同理可证Φ(a)= f(a);若x= b,取△x< 0,则同理可证Φ'(b)= f(b)定理2(原函数存在定理)设函数f(x)在区间[a,b|上连续,则积分上限函数Φ(x)=~f(t)dt就是f(x)在区间[a,b)|上的一个原函数定理的重要意义:(1)肯定了连续函数的原函数是存在的(2)初步揭示了积分学中的定积分与原函数之间的联系
定理2(原函数存在定理) 定理的重要意义: (1)肯定了连续函数的原函数是存在的. (2)初步揭示了积分学中的定积分与原函数之 间的联系. ( ) [ , ] ( ) ( ) ( ) [ , ] x a f x a b x f t dt f x a b = 设函数 在区间 上连续,则积分上限函数 就是 在区间 上的一个原函数. x a x a f a , 0 ( ) ( ) + 若 = = 取 ,则同理可证 ; x b x b f b , 0 ( ) ( ). − 若 = = 取 ,则同理可证

例:求下列函数的导数[,tf(t)dt , xf(t)dt , f*(x-t)f(t)dtso-层ar rom-I roa+()dx补充:如果f(t)连续,a(x),b(x)可导X则 Fi(x)=Jn*) f(t)dt的导数为F(x)==.(" ()dt = [b(x)1b(x)dx
( ) 1 ( ) ( ) ( ) ( ) ( ) b x a f t a x b x F x f t dt = 如果 连续, , 可导, 则 的导数为 d ( ) d x a xf t dt x d ( ( ) ) d x a x f t dt x = 补充: ( ) 1 ( ) ( ) [ ( )] ( ) b x a d F x f t dt f b x b x dx = = ( ) , ( ) , ( ) ( ) x x x a a a tf t dt xf t dt x t f t dt − 例:求下列函数的导数 ( ) ( ) x a = + f t dt xf x

DX证: 令u= b(x),则F;(x)= Jb(") f(t)dt=]" (t)dtlu=b(x)d.. F*(x) = ~J" (t)dt.:b(x)dxd= f(u)b'(x) = f[b(x)]b'(x)F: () - m, (0t= -Ia()2()类似的dcb(x)F'(x) =f(t)dt = f[b(x)]b'(x)- f[a(x)]a'(x)dxJa(x)xF,(x) =( I, + s)提示:f(t)dt
提示: ( ) ( ) 3 ( ) ( ) ( ) c b x a x c F x f t dt = + ( ) 3 ( ) ( ) ( ) [ ( )] ( ) [ ( )] ( ) b x a x d F x f t dt f b x b x f a x a x dx = = − 2 ( ) ( ) ( ) [ ( )] ( ) b a x d F x f t dt f a x a x dx = = − 类似的 1 ( ) ( ) ( ) u a d d F x f t dt b x du dx = = = f u b x f b x b x ( ) ( ) ( ) ( ) 证: ( ) 1 ( ) ( ), ( ) ( ) [ ( ) ] b x u u b x a a u b x F x f t dt f t dt 令 = = = 则 =

cosx例1 求lim2x-0十这是分析:型不定式,应用洛必达法则0ddecosx解dtdx JidxJcosx.(cosx)' = sinxe-cos*x-cos~xesinx·e-cos'xdtcosx= limlim2x2ex-0x-0
例1 求 lim . 2 1 cos 0 2 x e dt x t x − → 解 − 1 cos 2 x t e dt dx d , cos 1 2 − = − x t e dt dx d (cos ) 2 cos = − − e x x sin , 2 cos x x e − = 2 1 cos 0 2 lim x e dt x t x − → x x e x x 2 sin lim 2 cos 0 − → = . 2 1 e = 0 0 分析:这是 型不定式,应用洛必达法则
Pus'.arctan(1 + t)dt jdu0lim练习求极限dx-0x(1 - cos x)Cu221xarctan(1 + t)dt JduJo解 原式=2limI-cosx2tx-→02arctan(1 + t)dt= 2lim 0d3x?x-02arctan(1+x) ·2xlim32xx-→02元元634
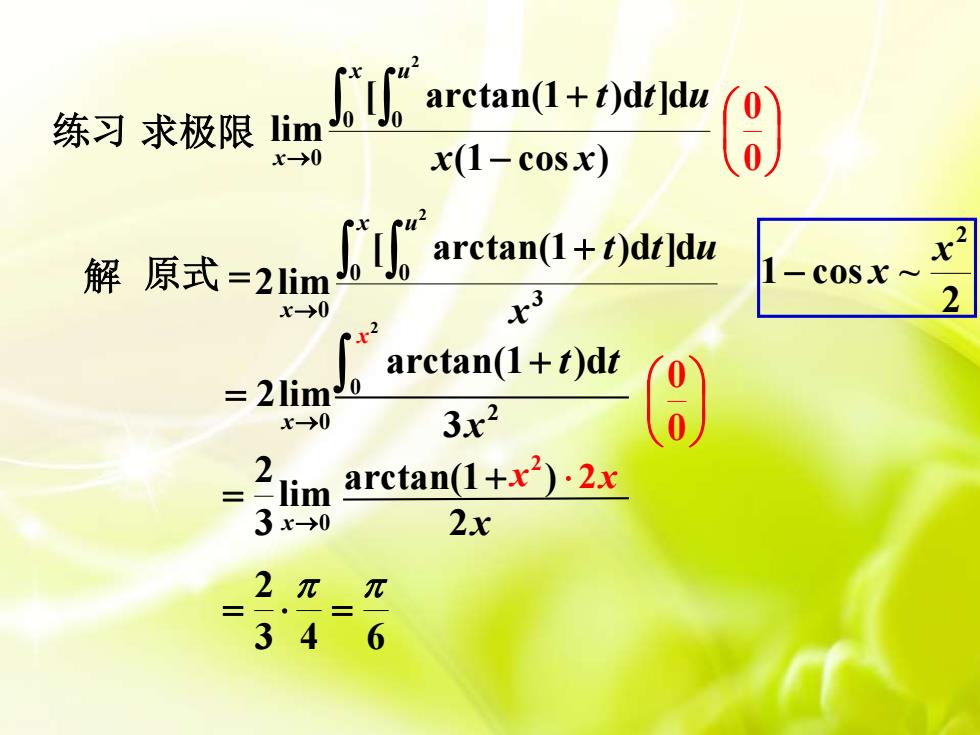
练习 解 求极限 (1 cos ) [ arctan(1 )d ]d lim 0 0 0 2 x x t t u x u x − + → 0 0 原式 = 3 0 0 0 [ arctan(1 )d ]d 2lim 2 x t t u x u x + → 0 2lim → = x 2 1 cos ~ 2 x − x 2 0 arctan(1 )d x + t t 2 3x 0 lim 3 2 → = x 2x arctan(1+ ) 2 x 2x 3 4 6 2 = = 0 0