
导期 【思考辨析】 判断正误.(正确的画“√,错误的画“×) ()点到直线的距离就是点和直线上任意一点之间的距离.( (2)若直线与平面平行,则直线到平面的距离即为直线上的任意 点到平面的距离.() (3)两平行平面的距离即为其中一平面上任意一点到另一平面的 距离() (4若空间两点已定,则它们之间的距离是定值.() (5)若直线与平面α湘交,则直线到平面a的距离无法确定.(
导航 【思考辨析】 判断正误.(正确的画“ ”,错误的画“×”) (1)点到直线的距离就是点和直线上任意一点之间的距离.( × ) (2)若直线与平面平行,则直线到平面的距离即为直线上的任意一 点到平面的距离.( ) (3)两平行平面的距离即为其中一平面上任意一点到另一平面的 距离.( ) (4)若空间两点已定,则它们之间的距离是定值.( ) (5)若直线l与平面α相交,则直线l到平面α的距离无法确定.( × )
导期 课堂·重难突破 探究一两点之间的距离及点到直线的距离 【例1】在二面角a-L-B中,ABCa,且AB⊥l, CDcf,CD⊥I,B,C∈L,且AB,CD的夹角为 60°,若AB=BC=CD=1,求A与D两点间的 距离 分析:A与D两点间的距离就是AD的模,即利用向量数量积的 性质|a=Vaa求向量的长度
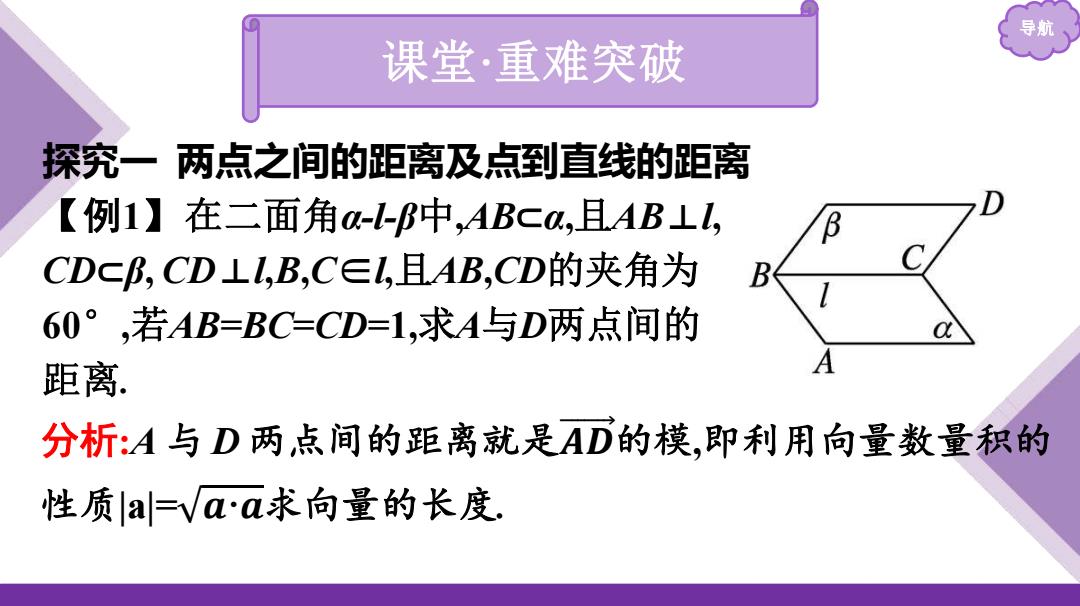
导航 课堂·重难突破 探究一 两点之间的距离及点到直线的距离 【例1】在二面角α-l-β中,AB⊂α,且AB⊥l, CD⊂β, CD⊥l,B,C∈l,且AB,CD的夹角为 60° ,若AB=BC=CD=1,求A与D两点间的 距离. 分析:A 与 D 两点间的距离就是𝑨 𝑫 的模,即利用向量数量积的 性质|a|= 𝒂·𝒂求向量的长度

导航、 解:,AB⊥L,.AB.BC=0. .CD⊥L,∴.BC.CD=0. .AB与CD的夹角为60°, .<AB,CD>=60°或<AB,CD>=120°. .AD =AB+BC+CD
导航 解:∵AB⊥l,∴𝑨 𝑩 ·𝑩 𝑪 =0. ∵𝑪 𝑫 ⊥l,∴𝑩 𝑪 ·𝑪 𝑫 =0. ∵AB 与 CD 的夹角为 60°, ∴<𝑨 𝑩 ,𝑪 𝑫 >=60°或<𝑨 𝑩 , 𝑪 𝑫 >=120°. ∵𝑨 𝑫 = 𝑨 𝑩 + 𝑩 𝑪 + 𝑪 𝑫

导 ADD=(AB+BC+CD)2= AB2+BC2+CD2+2AB-BC+2BC-CD+2AB-CD- 1+1+1+0+0+2 ABCDIc0S<AB,CD>= 2(<AB,CD>=60), V2(<AB,CD>=120). '.A与D两点间的距离为2或√2
导航 ∴|𝑨 𝑫 |= |𝑨 𝑫 | 𝟐 = (𝑨 𝑩 + 𝑩 𝑪 + 𝑪 𝑫 ) 𝟐 = |𝑨 𝑩 | 𝟐 + |𝑩 𝑪 | 𝟐 + |𝑪 𝑫 | 𝟐 + 𝟐𝑨 𝑩 ·𝑩 𝑪 + 𝟐𝑩 𝑪 ·𝑪 𝑫 + 𝟐𝑨 𝑩 ·𝑪 𝑫 = 𝟏 + 𝟏 + 𝟏 + 𝟎 + 𝟎 + 𝟐|𝑨 𝑩 ||𝑪 𝑫 |𝐜𝐨𝐬 < 𝑨 𝑩 ,𝑪 𝑫 > = 𝟐( < 𝐀 𝐁 ,𝐂 𝐃 >= 𝟔𝟎°), 𝟐( < 𝐀 𝐁 ,𝐂 𝐃 >= 𝟏𝟐𝟎°). ∴A 与 D 两点间的距离为 2 或 𝟐