导航 3.做一做:如图,正方体ABCD-A1B,C1D1的棱长为1,E是上底面 AB,C1D1的中心,则点E到平面ABC,D,的距离是 D C E。 A B B
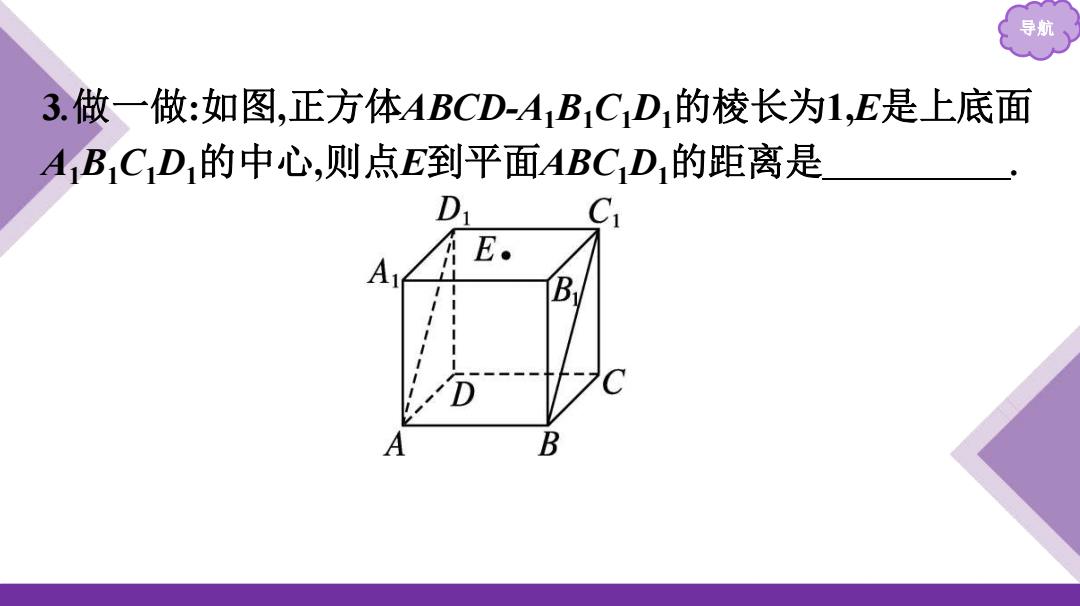
导航 3.做一做:如图,正方体ABCD-A1B1C1D1的棱长为1,E是上底面 A1B1C1D1的中心,则点E到平面ABC1D1的距离是

解析:如图,以D为坐标原点,以DA,DC,DD方向分别为x 轴、y轴、z轴正方向建立空间直角坐标系,则 D A E。 D0,00,410,0,E(321)4i(10,1 则A正=(221),DA(1,01 由题意知DA1为平面ABCD1的一个法向量 '.点E到平面ABCD1的距离 d-IAE-DAil 答案号 DAil 4
导航 解析:如图,以 D 为坐标原点,以𝑫 𝑨 , 𝑫 𝑪 , 𝑫𝑫𝟏 方向分别为 x 轴、y 轴、z 轴正方向建立空间直角坐标系,则 D(0,0,0),A(1,0,0),E 𝟏 𝟐 , 𝟏 𝟐 ,1 ,A1(1,0,1), 则𝑨 𝑬 = - 𝟏 𝟐 , 𝟏 𝟐 ,1 ,𝑫𝑨𝟏 =(1,0,1). 由题意知𝑫𝑨𝟏 为平面 ABC1D1的一个法向量, ∴点 E 到平面 ABC1D1的距离d=|𝑨 𝑬 ·𝑫𝑨𝟏 | |𝑫𝑨𝟏 | = 𝟏 𝟐 𝟐 = 𝟐 𝟒 . 答案: 𝟐 𝟒

导 四、相互平行的直线与平面之间、相互平行的平面与平面之 间的距离 【问题思考】 1.若直线I平面a,P∈L,Q∈L,则P,Q到平面a之间的距离有什 么关系? 提示:相等 2.若平面aI平面B,点P,Q是平面a内的任意两点,点P,Q到平面 的距离有什么关系? 提示:相等
导航 四、相互平行的直线与平面之间、相互平行的平面与平面之 间的距离 【问题思考】 1.若直线l∥平面α,P∈l,Q∈l,则P,Q到平面α之间的距离有什 么关系? 提示:相等. 2.若平面α∥平面β,点P,Q是平面α内的任意两点,点P,Q到平面 β的距离有什么关系? 提示:相等

3.填空:当直线与平面平行时,直线上一点到平面的距离 称为这条直线与这个平面之间的距离;当平面与平面平行时, 一个平面内一点到另一个平面的距离称为这两个平行平 面之间的距离.一般地,与两个平行平面同时 的直线,称为 这两个平面的公垂线,公垂线夹在平行平面间的部分,称为这 两个平面的公垂线段显然,两个平行平面之间的距离也等于 它们的 的长 直线与平面之间的距离和平面与平面之间的距离,都可以归 结成点到平面的距离,因此同样可以通过空间向量来求得
导航 3.填空:当直线与平面平行时,直线上任意一点到平面的距离 称为这条直线与这个平面之间的距离;当平面与平面平行时, 一个平面内任意一点到另一个平面的距离称为这两个平行平 面之间的距离.一般地,与两个平行平面同时垂直的直线,称为 这两个平面的公垂线,公垂线夹在平行平面间的部分,称为这 两个平面的公垂线段.显然,两个平行平面之间的距离也等于 它们的公垂线段的长. 直线与平面之间的距离和平面与平面之间的距离,都可以归 结成点到平面的距离,因此同样可以通过空间向量来求得

导航 4.做一做:在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=4,则 BD,到平面ABCD的距离为;平面AA1D1D到平面BBC1C的 距离为·
导航 4.做一做:在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1 =4,则 B1D1到平面ABCD的距离为4 ;平面AA1D1D到平面BB1C1C的 距离为 1