
30、《高等数学》(第七版)上册习题全解所以当x-0时(1-cosx)2是比sinx高阶的无穷小3.当x-1时,无穷小1-×和(1)1-x3(2)-一(1-x2)是否同阶,是否等价?1-x11-x1解(1)(x→1),同阶,不等价3231+x+x2(1-x)(1+x+x2)-1-x21-41(x-→1).同阶,等价(2)111+x-(1 -x2)(1 -x)(1 +x)224.证明:当x-0时,有x2(1)arctan x~x;(2)secx2证(1)令x=tant即t=arctanx,当x-→0时,t0因为tarctanxlim-=lim=1r-otan tx1--0所以(x→0).arctan x~x(2)因为2sin2x-21 cos xlimsec x-1=lim=lim22t22cos xcosx222sin?x21limlincos.所以→0)sec x325.利用等价无穷小的性质,求下列极限:(1) limtan 3xsin (x")(2)lim(nm为正整数);2x-0(sin x)"(3) liman x-sin xsin x-tan x(4)lim-sinxt-(+x2-1)(/1+sin x-1)3x3tan3x解(1) lim= lim22x1-02x1-00,n>m.sin (x")xn=lim(2)lim1,n=m,(sinx)m0xmo,n<m

31第一章函数与极限x221tan x-sin xsec x-(3)lim=lim= lim202sinxsin2x注,在作等价无穷小的代换求极限时,可以对分子或分母中的一个或若干个因子作代换,但不能对分子或分母中的某个加项作代换例如,本题中若将分子中的tanx、sinx均换成x,那么分子成为0,得出极限为0,这就导致错误的结果sin x -tan xsin x(1-sec x)=lim(4)lim12.1(i+x2-1)(1+sinx-1)sinx322=lim3t66.证明无穷小的等价关系具有下列性质:(1)α~α(自反性);(2)若α~β,则β~α(对称性):(3)若α~ββ~,则α~(传递性).证(1)因为lim%=1,所以α~α;αB=1,即β~α;(2)因为α~β,即lim=1,所以lim上BdB=1.所以O(3)因为α~ββ~,即lim=1,limβyβQaxaB=1,即α~lim= lim.lim=limββyYy习题1-8函数的连续性与间断点1.设y=(x)的图形如图1-11所示,试指出(x)的全部间断点,并对可去间断点补充或修改函数值的定义,使它成为连续点JA图1-11
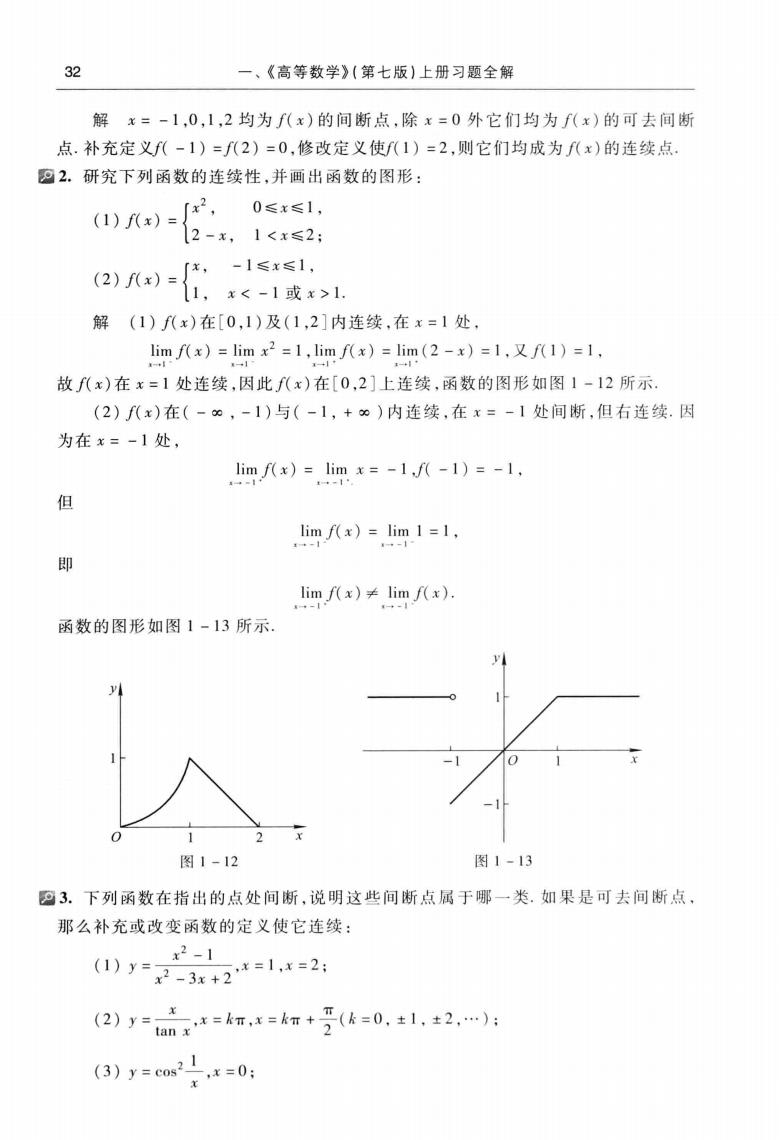
32、《高等数学》(第七版)上册习题全解解x=-1,0,1,2均为f(x)的间断点.除x=0外它们均为f(x)的可去间断点.补充定义f(-1)=f(2)=0,修改定义使f(1)=2,则它们均成为f(x)的连续点2.研究下列函数的连续性,并画出函数的图形:x20≤x≤1,(1) f(x):[2-x,1<x≤2;一x一,(2) F(x)=[,x<-1或x>11解(1)f(x)在[0,1)及(1,2]内连续,在x=1处,limf(x)=limx2=1,limf(x)=lim(2-x)=1,又f(1)=1,故f(x)在x=1处连续,因此f(x)在[0,2]上连续,函数的图形如图1-12所示(2)f(x)在(-0,-1)与(-1,+80)内连续,在x==1处间断,但右连续.因为在x=-1处,limf(x)=limx=-1,f(-1)=-1,但lim f(x) = lim 1=1,即limf(α)+limf(x),函数的图形如图1-13所示川yx-1o1012图1-13图1-123.下列函数在指出的点处间断,说明这些间断点属于哪一类.如果是可去间断点,那么补充或改变函数的定义使它连续:x?-1(1) y=+2-3x+2*x=1,x=2;3(h=0,±1,±2,);,x=T,x=kT+(2) y:tanx2(3) y= cos? |,x=0;x

33第一章函数与极限[x-1,x≤],(4) x=1[3 -x,x>1,解(1)对x=1,因为f(1)无定义.但x2 -1(x-1)(x+1)=limx+1lim=lim-2-2-3x+21-(x-2)(x-1)1x-2所以,x=1为第一类间断点(可去间断点),重新定义函数:x2-1x+1,2,2-3x+2fi(x)=-2.x=1,则f(x)在x=1处连续因为limf(x)=0,所以x=2为第二类间断点(无穷间断点)xX=lim-=1,所以x=0为第一类间断点(2)对x=0,因为(0)无定义,limotan x1-0X(可去间断点),重新定义函数:xAx+k,+tanx2(keZ),fi(x) =[1.x=0则f(x)在x=0处连续,Y对x=k(k=±1,±2,..),因为lim,所以x=k元(k=±1,±2,.)为tanx第二类间断点(无穷间断点)×_=0,而函数在k+号处无定义,所以×=对x=k+(keZ),因为lim2kwglanx2晋(heZ)为第一类间断点(可去间断点),重新定义函数:k+-2+x*h,kn+2tanxf2(x)=(heZ),T0,x=km+-2(keZ)处连续则J2(x)在x=+2(3)对x=0,因为1limcos2及1imcos2一均不存在,所以×=0为第二类间断点。X.l(4)对x=1,因为lim(x)=lim(3-x)=2,limf(x)=lim(x-1)=0,即左、右极限存在,但不相等,所以x=1为第一类间断点(跳跃间断点):注在讨论分段函数的连续性时,在函数的分段点处,必须分别考虑函数的左连续性和右连续性,只有函数在该点既左连续,又右连续,才能得出函数在该点

34一、《高等数学》(第七版)上册习题全解连续1-x2h4.讨论函数(x)=limx的连续性,若有间断点,则判别其类型*1+r2n解1xI>1.-x,1 - x2#f(x)=lim0,1x=1,1+x2mxx,1x1<1.在分段点x=-1处,因为limf(x)=lim(-x)=1,limf(x)= lim x=-1,limf(x)≠limf(x)所以x=一1为第一类间断点(跳跃间断点)在分段点x=1处,因为limf(x)=limx=1,limf(x)=lim(-x)=-1,limf(x)+limf(x)所以x=1为第一类间断点(跳跃间断点)。5.下列陈述中,哪些是对的,哪些是错的?如果是对的,说明理由:如果是错的,试给出一个反例(1)如果函数f(x)在a连续,那么(x)1也在a连续:(2)如果函数1f(x)1在a连续,那么f(x)也在a连续解(1)对.因为If(x)l-lf(a)Il≤lf(x)-f(a)l-→0(x-→a),所以|(x)1也在a连续(2)错.例如I.x≥0f(x)1,x<0.则1f(x)1在x=0处连续,面/(x)在x=0处不连续*6.证明:若函数f(x)在点xo连续且f(xo)≠0,则存在xo的某一邻域U(xo),当xEU(x)时(x)¥0xo)>08>0x证若(xo)>0,因为f(x)在xo连续,所以取=xo),即U(x0,)时,有1f(x)-f(x0)1<(x)(x)0<-(x0)