
26 第一章基■本■概■念 b+d<1. a+c 这不是M的一个关系,因为例如由于 鼎-41 故分照子,但是,之=子而 号-音<1 故又有子R子,即又有宁R子 这就是说,之与子是不是符合所规定的法则,是不确定 的. 下面要讨论一种特殊的关系,叫做等价关系 定义2如果集合M的一个关系R满足以下条件 I°对M中任意元素a都有aRa;(反身性) 2°如果aRb,必有bRa(对称性) 3°如果aRb,bRc,必有aRc,(传递性) 则称这个关系是M的一个等价关系· 等价关系常用符号~表示.当~b时,称a与b等价 由上节末直接可知,同构关系就是所有代数系统间的一个等 价关系 例5法则 aRb al b 虽是整数集Z的一个关系,但不是等价关系.因为虽然反身性 与传递性都成立,但对称性不成立,例如2|6,但682,即 26,但6. 例6令M为全校学生的集合,规定 aRb a与b同在一系」
b a R d c b+ d a + c < 1 . 这不是 M 的一个关系, 因为例如由于 1 + 3 2 + 2 = 4 4 = 1, 故 1 2 珚R 3 2 . 但是, 1 2 = 2 4 , 而 2 + 3 4 + 2 = 5 6 < 1, 故又有 2 4 R 3 2 , 即又有 1 2 R 3 2 . 这就是 说, 1 2 与 3 2 是不是 符合 所规 定的 法则, 是 不确 定 的 . 下面要讨论一种特殊的关系, 叫做等价关系 . 定义 2 如果集合 M 的一个关系 R 满足以下条件: 1° 对 M 中任意元素 a 都有 aRa; ( 反身性) 2° 如果 aRb, 必有 bRa; (对称性) 3° 如果 aRb, bRc, 必有 aRc, ( 传递性) 则称这个关系是 M 的一个等价关系 . 等价关系常用符号~表示 . 当 a~ b 时, 称 a 与 b 等价 . 由上节末直接可知, 同构关系就是所有代数系统间的一个等 价关系 . 例 5 法则 aRb a | b 虽是整数集 Z 的一个关系, 但不是等价关系 . 因为虽然反身性 与传递性都成立, 但对称性不成立, 例如 2 | 6, 但 6 8 2 . 即 2 R6, 但 6珚R2 . 例 6 令 M 为全校学生的集合, 规定 aRb a 与 b 同在一系 . 26 第一章 基■本■概■念

§6等价关系与集合的分类 27 这显然是M的一个等价关系· 例7令Z是整数集,任意取定一个正整数n,并规定 aRb a=b(mod n), 即a与b同用n除其余数相等,这显然是Z的一个等价关 系 定义3若把集合M的全体元素分成若干互不相交的子集 (即任二互异子集都无公共元素),则称每个这样的子集叫做M 的一个类;类的全体叫做M的一个类. 集合的分类与集合的等价关系间有密切的联系· 定理1集合M的一个分类决定M的一个等价关系 证对集合M的元素规定以下关系: aRba与b同在一类. 这显然是M的一个等价关系. 定理2集合M的一个等价关系决定M的一个分类. 证下面利用M的等价关系~来作出M的一个分类 任取a∈M,与a等价的一切元素作成M的一个子集,这个 子集记为泰.由于a~a,故 aE璇 因此,M中每个元素都一定属于一个类 下面再证每个元素只属于一个类. 设a∈陈a∈聊则 ab,ac. 任取x∈派则x~b.于是由上可得 b a,ac, 从而x~c即x∈聊.于是珔聊 同理可证聊珠.因此,琦=聊 这样,便把M的全体元素分成了互不相交的子集,因此, 这是M的一个分类
这显然是 M 的一个等价关系 . 例 7 令 Z 是整数集, 任意取定一个正整数 n, 并规定 aRb a≡b( mod n) , 即 a 与 b 同 用 n 除其 余 数 相 等, 这 显 然 是 Z 的 一 个 等 价 关 系 . 定义 3 若把集合 M 的全体元素分成若干互不相交的子集 (即任二互异子集都无公共元素 ) , 则称每个这样的子集叫做 M 的一个类; 类的全体叫做 M 的一个 类 . 集合的分类与集合的等价关系间有密切的联系 . 定理 1 集合 M 的一个分类决定 M 的一个等价关系 . 证 对集合 M 的元素规定以下关系: aRb a 与 b 同在一类 . 这显然是 M 的一个等价关系 . 定理 2 集合 M 的一个等价关系决定 M 的一个分类 . 证 下面利用 M 的等价关系~来作出 M 的一个分类 . 任取 a∈ M, 与 a 等价的一切元素作成 M 的一个子集, 这个 子集记为珔a . 由于 a~ a, 故 a∈珔a, 因此, M 中每个元素都一定属于一个类 . 下面再证每个元素只属于一个类 . 设 a∈珔b, a∈珋c, 则 a~ b, a~c . 任取 x∈珔b, 则 x~b . 于是由上可得 b~ a, a~c, 从而 x~ c, 即 x∈珋c . 于是珔b 珋c . 同理可证珋c 珔b . 因此, 珔b =珋c . 这样, 便把 M 的全体元素分成了互不相交的子集, 因此, 这是 M 的一个分类 . §6 等价关系与集合的分类 27

38 第一章基■本■概■念 证毕) 例8求由等价关系 aRb a=b(mod 4) 所决定的整数集Z的分类. 解由于任何整数用4除所得余数只能是0,1,2,3,故 由此可得Z的一个分类.它把Z分成四个类,它们是 {…,-8,-4,0,4,8,…}, …,7,-3,1,5,9…}, {…,-6,-2,2,6,10,…}, f…,-5,-1,3,7,11,… 如果用疑表示整数m所在的类,则以上四个类可表示成 0,1,2,3, 称它们是4为模的剩余类(或同余类).显然,两个整数a与b 同在一类,即菇-琢当且仅当4整除a与b的差 更一般的,可讨论以任意正整数n为模的剩余类 这种剩余类在以后各章还将作进一步讨论. 习题16 L.设M为整数集,规定 aRb 4|a+b. 问:R是否为M的一个关系?是否满足反身性、对称性和传递性? 2.设M是实数集.问以下各关系是否为M的等价关系? 1)aRb a≤b3)aRb a=b: 2)aRb ab0;4)aRb d+B≥0 3.试指出上题中等价关系所决定的分类 4.分别举出三个例子各满足等价关系中的两个条件,而另一个条件不 满足· 5.设M是任意非空集合,并令 R=((a.b)l a,bE M
(证毕) 例 8 求由等价关系 aRb a≡b( mod 4 ) 所决定的整数集 Z 的分类 . 解 由于任何整数用 4 除所得余数只能是 0 , 1, 2, 3, 故 由此可得 Z 的一个分类 . 它把 Z 分成四个类, 它们是 {…, - 8 , - 4 ,0 ,4 ,8 ,…} , {…, - 7 , - 3 ,1 ,5 ,9 ,…} , {…, - 6 , - 2 ,2 ,6 ,10, …}, {…, - 5 , - 1 ,3 ,7 ,11, …} . 如果用 珡m 表示整数 m 所在的类, 则以上四个类可表示成 0, 1, 2, 3, 称它们是 4 为模的剩余类( 或同余类 ) . 显然, 两个整数 a 与 b 同在一类, 即珔a =珔b 当且仅当 4 整除 a 与 b 的差 . 更一般的, 可讨论以任意正整数 n 为模的剩余类 . 这种剩余类在以后各章还将作进一步讨论 . 习题 1.6 1. 设 M 为整数集 , 规定 aRb 4 | a+ b . 问 : R 是否为 M 的一个关系 ? 是否满足反身性、对称性和传递性 ? 2. 设 M 是实数集 . 问以下各关系是否为 M 的等价关系 ? 1 ) aRb a≤b; 3) aRb a= b; 2 ) aRb ab≥0 ; 4) aRb a 2 + b 2 ≥0 . 3. 试指出上题中等价关系所决定的分类 . 4. 分别举出三个例子各满足等价关系中的两个条件 , 而另一个条件不 满足 . 5. 设 M 是任意非空集合 , 并令 R = {( a, b) | a, b∈ M} . 28 第一章 基■本■概■念

§6等价关系与集合的分类 29 证明:M的一个关系决定R的一个子集;反之,R的任一个子集决定M的 一个关系,且不同的关系决定R的两个不同的子集. 6.设A,B为集合M的任二非空子集,A与B'分别为A与B在M中 的余集,证明: 1)A-B=A0B'; 2)(AU B)-(An B)=(A-B)U(B-A) =(AU B)n(A'UB). 7.设中是集合X到集合Y的任意一个映射,A与B分别为X与Y的 非空子集.证明: 1)中'((4))A,且当中为单射时等号成立; 2)(中'(B)B,且当中为满射时等号成立 8设中是集合X到集合Y的一个映射,而A与B是X的任二非空子 集.证明: 1)MAUB)=A)U中(B): 2)AnB)A)nφ(B). 9.设o与t分别为集合A到B以及集合B到C的映射证明: 1)若0,t都是单射,则o是单射:反之,若0是单射,则。是单 射 2)若o,t都是满射,则o是满射;:反之,若0是满射,则T是满 射 10.设o是集合A到集合B的一个映射.证明: 1)o是单射 存在B到A的映射T,使to=1M; 2)0是满射 存在B到A的映射T,使oT=1B.其中14,1B 分别为集合A,B的恒等映射. 11.设o是集合A到集合B的一个映射.证明: 1)o是单射 对任意集合X到A的任意映射,互,若有 =05,必有1=5: 2)0是满射 对任意集合Y与B到Y的任意映射,飞,若有 西0=飞0,必有= 12.设A是一个非空集合,P(A)是A的幂集,即由A的一切子集作
证明 : M 的一个关系决定 R 的一个子集 ; 反之 , R 的任一个子集决定 M 的 一个关系 , 且不同的关系决定 R 的两个不同的子集 . 6. 设 A , B 为集合 M 的任二非空子集 , A′与 B′分别为 A 与 B 在 M 中 的余集 . 证明 : 1 ) A - B = A∩ B′; 2 ) ( A∪ B) - ( A∩ B) = ( A - B) ∪ ( B - A) = ( A∪ B) ∩ ( A′∪ B′) . 7. 设φ是集合 X 到集合 Y 的任意一个映射 , A 与 B 分别为 X 与 Y 的 非空子集 . 证明 : 1 ) φ- 1 (φ( A) ) A, 且当 φ为单射时等号成立; 2 ) φ(φ- 1 ( B) ) B, 且当 φ为满射时等号成立 . 8. 设φ是集合 X 到集合 Y 的一个映射 , 而 A 与 B 是 X 的任二非空子 集 . 证明 : 1 ) φ( A∪ B) = φ( A)∪φ( B) ; 2 ) φ( A∩ B) φ( A)∩φ( B) . 9. 设σ与τ分别为集合 A到 B 以及集合 B到 C的映射 .证明: 1 ) 若σ, τ都是单射 , 则 τσ是单射 ; 反之 , 若 τσ是单射 , 则 σ是单 射 ; 2 ) 若σ, τ都是满射 , 则 τσ是满射 ; 反之 , 若 τσ是满射 , 则 τ是满 射 . 10. 设σ是集合 A 到集合 B 的一个映射 . 证明 : 1 ) σ是单射 存在 B 到 A 的映射τ, 使τσ= 1A ; 2 ) σ是满射 存在 B 到 A 的映射 τ, 使στ= 1B . 其中 1A , 1 B 分别为集合 A , B 的恒等映射 . 11. 设σ是集合 A 到集合 B 的一个映射 . 证明 : 1 ) σ是单射 对任意集合 X 到 A 的任意映射 τ1 , τ2 , 若有στ1 =στ2 , 必有τ1 =τ2 ; 2 ) σ是满射 对任意集合 Y 与 B 到 Y 的任意映射τ1 , τ2 , 若有 τ1σ=τ2σ, 必有τ1 =τ2 . 12. 设 A 是一个非空集合 , P( A) 是 A 的幂集 , 即由 A 的一切子集作 §6 等价关系与集合的分类 29
30 第一章基■本■概■念 成的集合.证明:在P()与A间不存在双射 提示:反证法.若有双射中,可考虑 A=((M)ME P(A),(M)EM
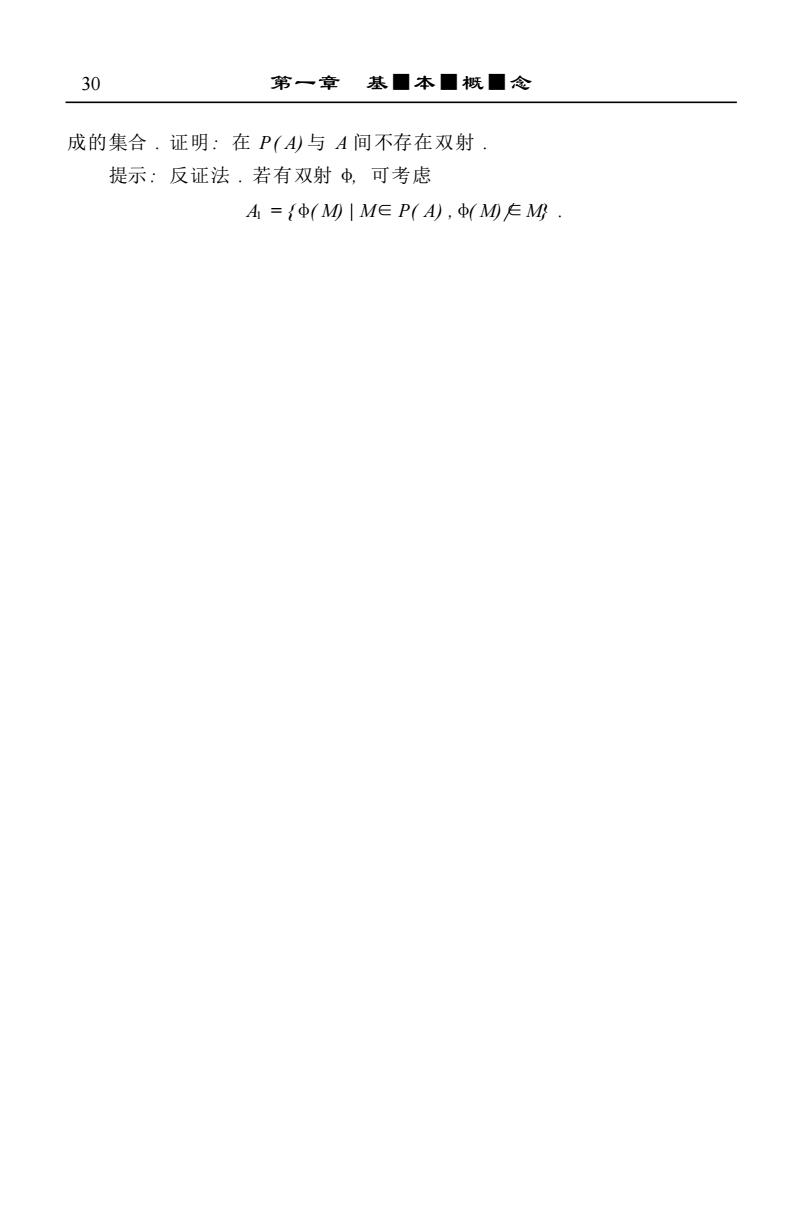
成的集合 . 证明 : 在 P( A) 与 A 间不存在双射 . 提示 : 反证法 . 若有双射 φ, 可考虑 A1 = {φ( M) | M∈ P( A) ,φ( M)/∈M} . 30 第一章 基■本■概■念