
14 线性代数·复变面数·展率统计习延全解(下爵)● 第一章率论的基本板念·习题全解 15 (2P(B=Pa,)-P(aP(a1a)=是×音-品-希 B:构成一个划分.A=“从乙袋中取得白球”,由全概率公式 (3)P(C)=P(AA:U AA)-P(AA)+P(AA:)+ P(A)-P(AIB)P(B)+P(AIB:)P(B:) P((AA:)(AA)) P(A)P(A:A)+P(A)P(A:A)+0 0°19(2) 第一只盒子装有5只红球,4只白球第二只盒子装有4只红球 -是×号+品×号-将 5只白球.先从第一只盒子中任取2只球放入第二只盒子中去,然后从第二只众 (4)P(D)=P(A2UA1A2)=P(A:A)+P(A1) 子中任取一只线,求取到白球的概率 P(A不)(A1A2) 解 设B一“从第一个套中取到只白球”d一0,12.则BB,B构吸 P(A)P(A:IA)+P(A)P(A)-o 一个划分,设A■“从第二个盒中取得白球”,则由全概率公式知 P(A)=P(AIB)P(B)+P(AB)P(B)+P(AIB:)P(B:) 1 -品×+品×号= 22.18某人忘记了电话号码的最后一个数字,因而他意地拔号,求他 -音·得+品+品得 - 姿号不超过三次而装遵所需电话的概率,若已知最后一个数字是奇数,那么此 250设一人群中有37.5%的人血型为A型,20.9%为B型,33.7为为 概率是多少? O型,7.9%为AB型,已知能允许输血的血型配对如下表,珑在在人群中任选一 解法1 设一“第次接通电话”(=1,2,3),A一“拨号不超过3次接 人为血者,再任选一人为需要输血者,阿输血阻成功的概率是多少? 通所需电话”,则A一A:U石A:U瓦AA,故所求概率 P(A)P(A)+P(AiA:)+P(Ai A,) 受血者 血者A型B型AB型O型 -品+是×号+品×8×是-高 AB型 解法2“拨号不超过3次就接通”的对立事件是“竣号3次都未接通”,于 0型 是 P(A)=1-P(不)-1-P(A) √:允许输血 ×:不允许输血 =1-P(不)P(不引)P(引本A) -1-品×8×日=品 设A,AA,A4分别为A,B,O,AB型输血,B,B,B,B,分别为 A,B,AB,O敌受血,则 设B一“已知最后一个数字悬奇数,不超过3次我通”,划 P(输血成功)-P(A1UAUA,UA)n(B1UB:UBUB,) P(B)=1-P(-1-号×是×号=是 =P(ABU.UA1B4UAB,U.UA:B:UAB1U 23°0授中有10个球,9个是白球,1个是红球,10个人依次从袋中各取一 UAB,UA,B1U.UA,B,) 球,每人取一球后不再放回授中,同第一人,第二人,.后一人取得红球的 -P(A:B)+P(A B)+P(A:B:)+P(A:B)+ 概率各是多少? P(A B)+P(A B)+P(A B)+P(A0 解此事件可归结为10个人排好位置,把10个球排好后每人分一个,所 =P(A)·P(B)+P(A)·P(B,)+P(A:)·P(B)+ 以红球在每个位置等可能地出魂,都为 P(A:)·P(B)+P(A)·P(B)+P(A)·P(B)+ P(A)·P(B)+P(A)=61.98% 分段提示第2419(1)一第3734题,用全概率公式、贝叶斯公式、事 0.20某种产品的商标为“MAXAM”,其中有2个字母脱落,有人捡起随 件的玻立性、解“全”与“贝”题,对“划分”婴有灵敏的感觉“独”可由实际本身 意放回,求放回后仍为“MAXAM"的概率, 判断,本压记忆,“职的摄一框的积”, 解字母股落2个共有五种情况,税下"M,X”或“A,X”成“M,A”或“A, 24°19(1)设有甲,乙两授,甲袋中装有:只白球、m只红球,乙袋中装有 N只白球、M只红球,今从甲授中任意取一只球放入乙授中,再从乙楼中任意取 A"或“M,M"分别用A1,A,A,A4,A,表示,则A,一12,5构成分:设且 =“放曰结果正晚”, 一只球,问取到白球的率是多少? 脱落的基本事件总敷为C一10, 要点从题中“嗅出”刻分,把“全”公式写出来,剩下就前单了。 解(1)设B1=“从甲按中取到白球”,B一“从甲袋中取得红球“,则B P(A)=P(A)-0P(A)-P(A)P(As)=1

16 线性代数·复变函数·展率统计习通全解(下卧)物 第一章率论的基本之·习题全解 17 P(Bla)-d=12,3,P(B1A)=1i=4.5 0.98×号 由全版率公式P(B-2P(A)P(BA) 00x音+a1x子~器 29.24有两箱同种类的零件,第一箱装50只,其中10只一等品:第二箱 -是×(品+品+)+1×(品+)-号 装30只,其中18只一等品,今从两箱中任桃出一箱,格后从该箱中致零件两次, 26°21已知男人中有5%是色直患者,女人中有0.25%是色官患者,今 每次任取一只,作不放目抽样,试求(1)第一次取到的零件是一等品的氯率:(2) 从男女人数相等的人群中随机地挑选一人,恰好是色盲惠者,问此人是男性的 第一次取到的学件是一等品的条件下,第二次取到的也是一等品的概半, 图率县多巾 解设B=“零件取白第4箱“,/一1,2: 要点“条件互倒”联想“见”:公式右边一中转/全:抓住刻分:死记贝叶 A=“第j次取出一等品”=12 斯公式不如章塑其推导过程 (1)求P(A)=? 设A一“色盲患者“,B=“男性”,则五=“女性”,B与B为划分,由贝 B1构成划分,由金餐率公式有 P(A)-P(A:IB)P(B)+P(A:B:)P(B:) =(10/50)×1/2)+(18/30)×(1/2)=2/E =a5×Q5+05义0.0z5-器 (2)求P(A:A)=? 0.22一学生接连参加同一课程的两次考试,第一次及格的概率为P,若 PCA:lA)-Pf 第一次及格,则第二次及格的率也为P若第一次不及格,则第二次及格的复 率为/2.(1)若至少有一次及格则他能取得某种资格,求他取得该资格的概 由(1)知:P(A)-,以下求P(AA)= 率,(2)若已知他第二次已轻及格,求他第一次及格的餐率。 B1,B构成划分,由全版率公式有 解没A一第次及络”,广三12 P(AA:)=P(AA:IBi)P(B:)+P(AA:IB:)P(B:) =[(10/50)×(9/49)]×1/2)+[18/30)×(17/29)]×(1/2) =0.19423 (1DP(AA:U④A:UA:A) =P(A)P(A:IA)+P(Ai)P(A:I )P(A)P(A) 于是Pa)-P=092=0486 28.25某人下午5:00下班,他所积熏的资料表明 =p·p+1-p)·号+p(1-p)-号p-号 到家时网5n35~539540-5445145-54495:30-5454迟于554 2PAlA)-PAPA+PCAP(A:l A而 P(ADP(A:Ap) a10 a25 a15 0.05 P。户 乘人车到 家的框率 a36 a35 20 a10 0.05 其中P(A)-P(AS)-P(A(AUA)=PCAA)+P(A,A:) =P(A)P(A:IA)+PC)P(A:IA) 某日他抛一枚硬币决定乘地铁还是乘汽车,结果他是5:47到家的,试求他 27心23将两信息分别编码为A和B传通出去,接收站收到时,A被误收 是乘地铁回家的餐半。 做B的服率为0.02.而面B被误收做A的餐率为0.01,信息A与信息B传送的频 解设B1一“乘地铁回家“,B1=“乘汽车回家”,A=“5145一549回 装程度为2:1,若楼收站收到的信息是A,问原发信息是A的景率是多少? 家.B,UB-S,BnB=,BB为划分.然硬币→P(B)=P() 解投B1=“发出信息A”.B=“发出信息B”,A=“收到信息为A”,则 0.5,由贝叶紧公式知 B,UB=S,B,B:=②,B,B为划分,由贝叶断公式 P()-F((B PAIB)·P(B P,A)=PA-+PAP(面 =0.45x0.5+0.2×0.5-
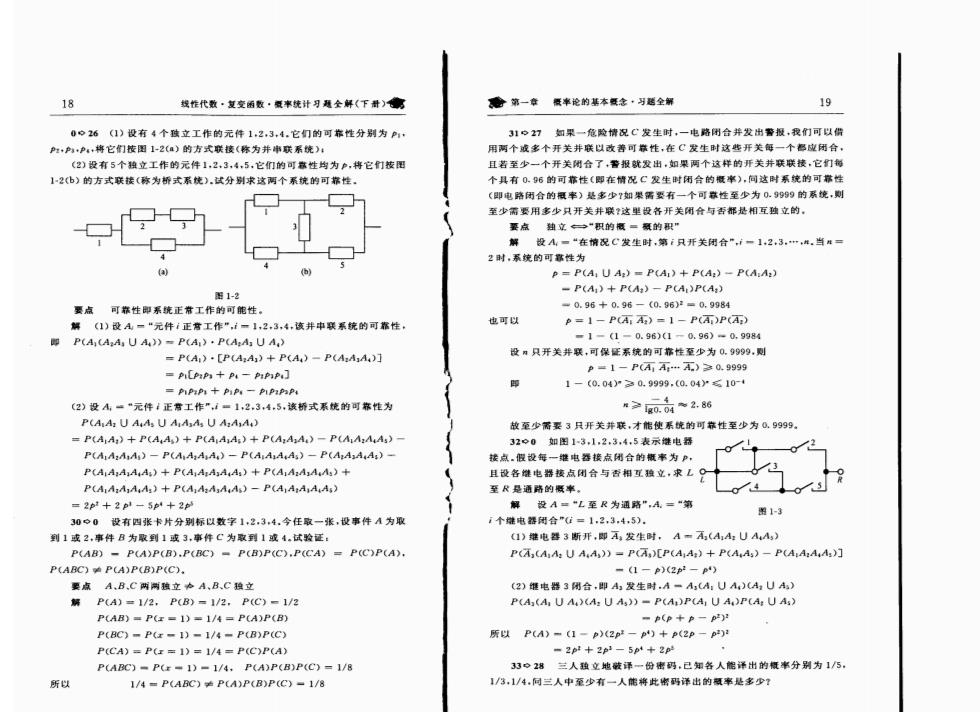
18 找性代数·复变函数·复率统计习避全解(下哥)像 意第一章 率论的基本念·习全解 19 026(1)设有4个独立工作的元件1.23,4.它们的可靠性分别为P1: 3127如果一危险情况C发生时,一电路闭合并发出警报,我们可以份 P1·产P,将它们按图1-2(a)的方式联接(称为并审联系统): 用两个或多个开关并联以改著可推性,在C发生时这些开关每一个都应闭合, (2)设有5个独立工作的元件1,2,3,4,5,它们的可靠性均为P,将它们按图 且若至少一个开关闭合了,报就发出,如果两个这样的开关并联联接,它们每 12(b)的方式联接(称为桥式系统)试分别求这两个系统的可靠性 个具有0.6的可靠性(即在情况C发生时闭合的概率),问这时系统的可靠性 (即电路闭合的概率)是多少?如果需要有一个可靠性至少为09999的系统,则 至少需要用多少只开关并联?这里设各开关闭食与否都是相互独立的, 要点轴立→“积的概=额的积” 解设A一“在慎况C发生时,第:只开关闭合”一1,2,3,当= 2时,系统的可富性为 p=P(A:U A:)P(A)P(A:)-P(A:A:) 图1-2 -P(A)+P(A)-P(A)P(A:) 要点可靠性即系统正常工作的可能性 -0.96+0.96-(0.96)2=0.9984 解(1)设A一“元件i正湾工作“,i一1,2,3,4,该并申联系统的可靠性, 也可以 P=1-P(AA)=1-P(不)P(A) 即P(A(AaA,UA)=P(A)·P(AAUA,) -1-(1-0.96)(1-0.96)-0,998 P(A).[P(A:A)+P(A)-P(A:AA)] 设m只开关并联,可保匠系统的可靠性至少为0.9999.则 p=1-P(AA-五)≥0.9999 PICPIPs+P-PiPiP] =PmP十P1一P的P 1~ (0.04)”≥0.9999.(0.0410- (2)设A=“元件4正霄工作”1=1,2,3,4.5,该桥式系统的可靠性为 >0.4*2.86 P(AIA:U A,U AAAs U A:AiA) 故至少需要3只开关并联,才能使系统的可靠性至少为0.9999 =P(AA:)+P(AA)+P(AAA:)+P(A:AA)-P(AA:AAs)- 32⊙0如图1-3,1,2,3,4,5表示鞋电得 P(AA:AA)-P(AAAA)-P(AAAAs)-P(A:AAA:)- 按点.假设每一维电器接点闭合的概事为P P(AIA:AAA)+P(AAAAA)F P(AIA:AAM:)+ 且设各继电器接点闭合与否相互独立,求L日 P(AA:AAA:)+P(AA:AAA)-P(AA:AAA) 至R是通路的概率。 4 =22+2p1-5p*+2 解设A=“L至R为通路”,A.=“第 1个继电器闭合”=1.2,34,5). 图1-3 30.0设有四张卡片分别标以数字1,23,4,今任取一张,投事件A为取 到1或2,事件B为取到1或3,事件C为取到1或4.试验证 ()继电器3断开,即A发生时,A=不(A1A:UA,A) P(AB)P(A)P(B).P(BC)-P(B)P(C).P(CA)P(C)P(A). P(A,(AA:U AA))=P(A)[P(AA:)+P(AA3)-P(AA:AA3)] P(ABC)P(A)P(B)P(C). =(1-P)(22-P4) 要点A.B,C两两独立A,B、C独立 (2)维电器3闭合,即A发生时.A一A,(A:UA)(A,UA) 解P(A)=1/2,P(B)=1/2,P(C)-1/2 P(A(A U A)(A:UA3))-P(A)P(A:UAP(A:U As) P(AB)-P(r -1)-1/4=P(A)P(B) -P(P+) P(BC)-P(x-1)-1/4-P(B)P(C) 质以P(A)-(1-p)(2p2-p)+p(2p-p2) P(CA)=P(=1)=1/4=P(C)P(A) =21十2p3一5p1+23 P(ABC)-P(x-1)-1/4,P(A)P(B)P(C)=1/8 33.2塔三人致立地译一份密码,已知各人帽译出的概常分别为1/5, 所以 1/4=P(ABC)P(A)P(B)P(C)-1/8 1/3,1/4.同三人中至少有一人能将此密码译出的减率是多少?

20 线性代数·复变函数·概率统计习题全解(下册)家 第一章 概率论的基本念·习题全解 21 罢点“至少”→对立事件。 -(2/5)3+(2/5)1+(1/5)1=17/125 解 三人能否得出相互独立,则三人都译不出的概率为 (4)投D一“这3个电话打的不相同的人”,在某一时间段打进3个电话,是 (1-1/5)(1-1/3)(1一1/5)-04,至少个择出的概率为1-0.4=0.6. 有瓶序的,则所求率为 0.29设第一只盒子中装有3只蓝球,2只绿球,2只白球,第二只意子中 P(D)=(2/5)×(2/5)×(1/5)+(2/5)×(1/5)×(2/5)+ 装有2只蓝球,3只绿球,4只白球,独立地分别在两只盒子中各取一只球 (2/5)×(2/5)×(1/5)+(2/5)×(1/5)×(2/5)+ (1)求至少有一只蓝球的概常:(2)求有一只蓝球一只白球的概率, (1/5)×(2/5)×(2/5)+(1/5)×(2/5)×(2/5) (3)已知至少有一只蓝球,求有一只蓝球一只白球的摄率, =6×(4/125)-24/125 解设AA:A分别表示在第一只盒子中取到蓝球绿球、白球B,B: (5)此小题是求3个电话都打给B的条件下,而B却都不在的条件展率,设 B,分别表示在第二只盒子中取到的盛球,绿球,白球。 E=“B都不在”,事件C,同(3),则所求条件概率为 (1)P(A:UB)P(A)+P(B)-P(AB) P(EC)-P(E)-(1/4)1-1/64 =3/7+2/9-3/7×2/9-35/63=5/9 34⊙3】袋中装有两只正品硬币,n只次品硬币(次品硬币的测面均印有因 (2)P(AB:U AB)=P(A B)+P(A;B) 徽),在较中任取一只,将它投掷r次,已知每次都得到国最,问这只硬币是正品 =3/7×4/9+2/7×2/9-16/63 的概率为多少? 解设B1=“任取一只,为正品”,B一“任取一只,为次品”,A一“将取到 030A,B.C三人在同一办公室工作.房间里有一廊电话.据统计知,打 的硬币抛n次,全为国数”,以下求P(BA)一? 给A,B.C的电话的领率分别为2/5,2/5,1/5.他们三人常因工作外出,A,B,C B,B:构成一个划分,可用贝叶断公式。 三人外出的展率分别为1/2,1/4,1/4.设三人的行动相互独立,求 (1)无人接电话的概率:(2)被呼叫人在办公室的报率。 PCA)-FAT 若某一时间段打进3个电话,求 (3)这3个电话打给问一个人的概率 (4)这3个电话打给不相同的人的概率: 032设一枚探水炸弹击沉一潜水艇的概率为1/3,击伤的概率为1/2, (5)这3个电话都打给B,而B却都不在的领率, 击不中的展率为1/6,并投击伤两次也会导致潜水艇下沉.求释4枚深水炸 解设A=“第i人被呼叫”,-1,2,3分别对应A,B,C,设B;=“第) 能击沉潜水艇的概率,(提示:先求出击不汽的展率,) 人在办公室",1=1,2,3分别对应A.B.C,则 解设A一“释救4枚炸弹,击沉潜水艇”,B=“释故4枚炸弹,均未击中 P(A)=2/5.P(A:)-2/5,P(A)-1/5 潜水艇,C一“释放4枚炸弹,恰有一枝击伤潜水”,则ABUC P(E)-1/2,P(B)=1/4,P(B)=1/4 由魏立性有P(B)=(1/6)·,P(C)=C!·(1/2)(1/6)1 P(B)=1/2.P(B)=3/A.P(B)-3/4 P(A)=1-P(A)=1-P(BUC)-1-P(B)-P(C) (1)无人接电话表明三人都外出了,所求概率为 =1-(1/6)·-C·(1/2)(1/6)=1283/1296 P(B,B,B)=P(B)P(瓦)P(B)-(1/2)×(1/4)×1/4)=1/32 35⊙0甲,乙、丙三人同时对飞机进行射击,三人击中的概率分别为0.4: (2) P(A B,U A:B:UAB)=P(A:B)+P(A:B:)+P(ABs) 0.5,0,7.飞机被一人击中而被击落的展率为02,被两人击中而被击落的低水 P(A)P(B)+P(A:)P(B:)+P(A)P(B) 为Q6,或三人都击中,飞机必定被击落,求飞机被击落的摄常, -(2/5)×(1/2)+(2/5)×(3/4)+(1/5)×(3/a)-13/20 解令A一“飞机被1人击中”一1,2,3,则 (3)设C一“3个电函都打给第4人“,=1,2,3分别对应A.B,C.所求瓶 A一A,不之m+不,A2不病+不,不2A辆 率为P(CUC2UC)-P(C)+P(C)+P(C) A:-AAz万+A,不A+A,AzA =[P(A)P+[P(A)P+[P(A)] A=AgA之A

22 线性代数·复变函数·概率统计习题全解(下册) 其中,A,表示被甲击中,A,表示设有被甲击中,依次类推,则有 P(A)P(A Az An)+P(A Az An)+P(A Az Ax)=0.36 P(A)=P(AAz万)+P(A万zA)+P(,AzA)=0.41 P(A)=P(A甲AzAw)-Q.14 第二章 随机变量及其分布 再令A一“飞机被击落”,则由全概率公式得 P(A)=P(AIA)P(A)+P(ALA:)P(A:)+P(AIA)P(A) =0.2×0.36+0.6×0.41+0.14×1=0.458 “人的是了不起的,只要专注干莱二率业二定会薇出使自已 36.33投根据以往记录的数据分析,某船只运输的某种物品损杯的情况 感到吃惊的成绩米。 共有三种:损坏2%(这一事件记为A1),损坏10%(事件A:,损坏90%(事件 A).且知P(A)-0.8,P(A)-0.15.P(A)=0.05.现在从已被运输的物品 马克·吐沮 中随机地取3件,发现这3件都是好的(这一事件记为B).试求P(A,|B), P(A:B),P(AlB)(这里设物品件数很多,取出一件后不影响取后一件是否为 商导学 好品的概率)。 要点由0.8十0.15+005=1,联想到A1,A:,A,为划分. 引微入概工程之一维篇 解验正划分的两条1“A1UA:UA3-5:2A1·A:一,A·A-, 人们不可能仅仅阀足于只用排列姐合和加诚乘除来计算概率,而这正是第 4·A,一可,由贝叶断公式 一章的局限所在,本章成功地实现了两大“空间站”:《概率论》与《微积分》的大 PCAI)RTAD RAFAFA) 对接随着求导、求积分等工具的介人《概率论》发生了脱胎换骨的大变化。 本章引进了一元微机分,下章将引进多元微积分,第二、三章的主题:引《微 (1一2%)1·0.8 -1-2%·0.8+1-10%·0,15+(1-90%)·0.05 积分》的水”来解《概率统计》的“渴”一简称引微入概工程. ✉0.8731 本章从1介绍随机变量.到§4出现了《微积分》的帮本公式,F(x) 同样可求 P(A:|B)≈0.1268,P(AlB)s5.798×10- F()=广fx)d及F"()-fx),"红旗集”通水了 37⊙34将A,B,C三个字母之一输入信道,输出为原学母的展率为a,而 这一杰出工作的完成,以人幻认识到随机变量这一概念为前摄条件。当S 输出为其他一字母的概率都是(1-)/2.今将字母申AAAA,BBBB,CCCC之 一输入信道,输入AAAA,BBBB,CCCC的率分别为:,P,P(十P:+ 一(正,反}时,是(正)或反dx均亲无意义.于是人们试图用指定买敏来标识 一1),已知输出为ABCA,问输人的是AAAA的概率是多少(设信道传输每个 样本点的方陆,使S与R相关联,终于找到了随机变量这个重要概念,陆机变量 学母的工作是相互独立的)? 是现代疑率论中最重要的概念。 解设事件B1,B,B分别为输人AAAA,BBBB,CCCC,面A为输出 随机变量的定义:由样本空S到实数集R的任一单值映射X=X(),均 ABCA,则B,B,B构成划分,由贝叶斯公式 可称作一个随机变量, P(AB)·P(B1) 只要符合定义,随机变量可以随意构造.由于事先不能确定5中一元素 PB,IAN-Pa·PBp+PABP(B)+PABD·PB万 一定出现.因而电不能事先确定X一X()一定收哪个实数.但是,一且给定 个具体的随机变量X=X()后,这种对应关暴本身是确定的,不随机 2·A+2m+2 本学科从此守上了随机变量这双“红舞鞋”,此后再也设聪下来, 请关注下面的文字, -2A1+aO(P4+P=3a-0+1-。 用X表示事件的方法:用X的像集所对应的原像集表示事件.因为【X(: ∈L)二S,所以{elX()∈表示随机事件,即用X的值城中的点集L二R所 对应的定义中的点集eX(e)∈L)来表示事件将{eX(e)∈L)简记为(X