
数学建模与数学实验 插值
数学建模与数学实验 插 值

实验目的 1.了解插值的基本内容, 实验内容 [1]一维插值 [2]二维插值 「3]实验作业
实验目的 实验内容 1.了解插值的基本内容. [1]一维插值 [2]二维插值 [3]实验作业
一维插值 一、插值的定义 二、插值的方法 拉格朗日插值 分段线性插值 三次样条插值 三、用MATLAB解插值问题 返回
拉格朗日插值 分段线性插值 三次样条插值 一 维 插 值 一、插值的定义 二、插值的方法 三、用MATLAB解插值问题 返回

二维插值 一、 二维插值定义 二、网格节点插值法 最邻近插值 分片线性插值 双线性插值 三、用MATLAB:解插值问题 网格节点数据的插值 散点数据的插值 返回
返回 二维插值 一、二维插值定义 二、网格节点插值法 三、用MATLAB解插值问题 最邻近插值 分片线性插值 双线性插值 网格节点数据的插值 散点数据的插值
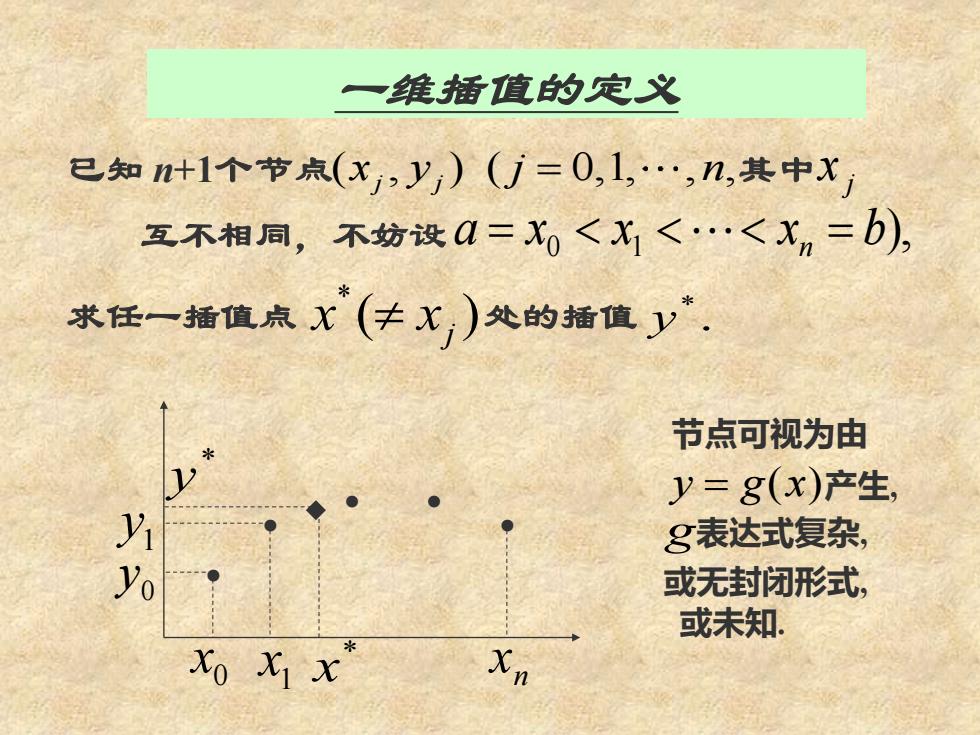
一维插值的定义 已知n+1个节点(x1,y)(j=0,1,.,n,其中xj 互不相同,不妨设a=X0<X1<<Xn=b), 求任一插值点X(卡X)处的插值y, 节点可视为由 1 y=8(x)产生, 8表达式复杂, Yo 或无封闭形式, 或末知 XO Xx Xn
一维插值的定义 已知 n+1个节点 ( , ) ( 0,1, , , j j x y j n = 其中 j x 互不相同,不妨设 ), 0 1 a x x x b = n = 求任一插值点 ( ) * j x x 处的插值 . * y • • • • • 0 x 1 x n x 0 y 1 y 节点可视为由 y = g(x) 产生, g 表达式复杂, 或无封闭形式, 或未知. ◆ * x * y