试验次数n 3000 5000 1万 2万 3万 国徽朝上 0.5040 0.5006 0.4879 0.4999 0.5046 频率 国徽朝下 0.4960 0.4994 0.5121 0.5001 0.4954 频率 试验次数n 5万 10万 100万 100万 1亿 国徽朝上 0.5021 0.4999 0.4999 0.5001 0.5000 频率 国徽朝下 0.4979 0.5001 0.5001 0.4999 0.5000 频率 可见当n→o时,fn(A)=P(A 7/21
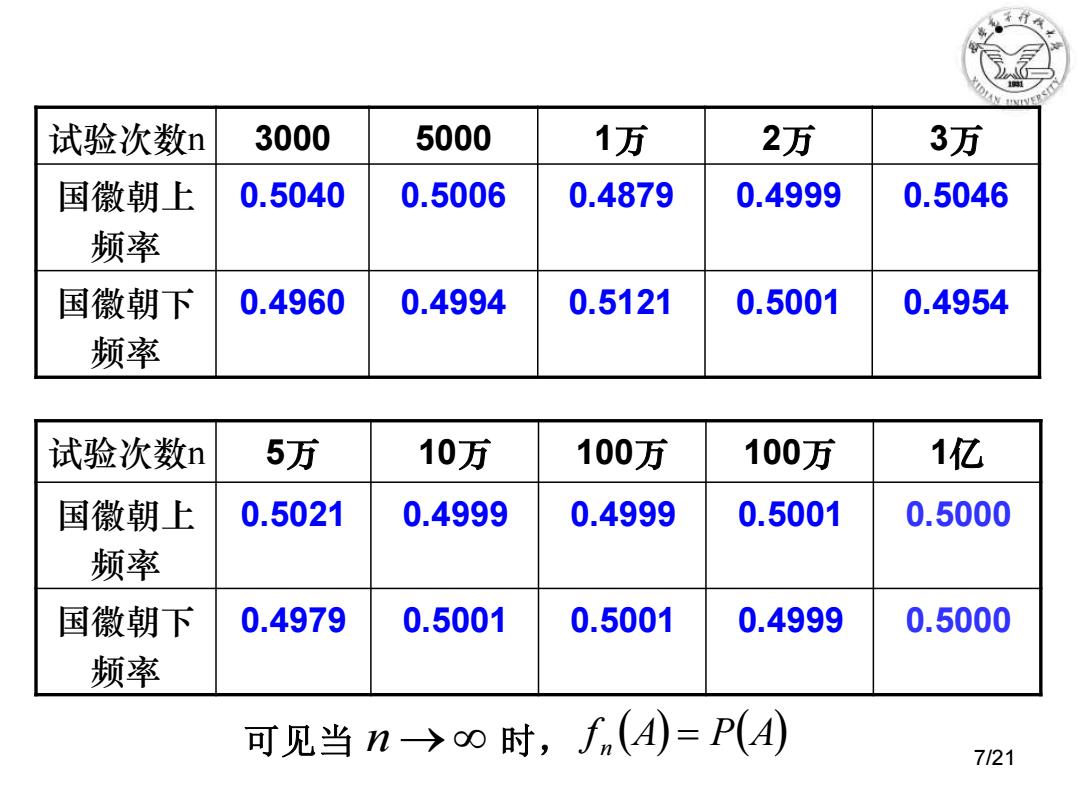
试验次数n 3000 5000 1万 2万 3万 国徽朝上 频率 0.5040 0.5006 0.4879 0.4999 0.5046 国徽朝下 频率 0.4960 0.4994 0.5121 0.5001 0.4954 试验次数n 5万 10万 100万 100万 1亿 国徽朝上 频率 0.5021 0.4999 0.4999 0.5001 0.5000 国徽朝下 频率 0.4979 0.5001 0.5001 0.4999 0.5000 f (A) P(A) 可见当 n → 时, n = 7/21

。实验3用频率估计自然对数e 。某班有个人,每人各有一支枪,这些枪外形一样。某次夜间紧急 集合,若每人随机地取走一支枪,求没有一个人拿到自己枪的概率? 解:记事件4为第个人拿到自已枪,事件A,为第个人没拿到自己枪, 易知: 。p4)=;Pa)=",=12,n n 0】 又记p为没有一个人拿到自己枪的概率。 以a瓦)=1-P04 由乘法公式可知 PlA)上P氏4PA)0s1<js )-4)r4)2ik) P444)广 8/21
实验3 用频率估计自然对数e ⚫ 某班有n个人,每人各有一支枪,这些枪外形一样。某次夜间紧急 集合,若每人随机地取走一支枪,求没有一个人拿到自己枪的概率? 解:记事件Ai为第i个人拿到自已枪,事件 为第i个人没拿到自己枪, 易知: ⚫ ; , ⚫ 又记 p0为没有一个人拿到自己枪的概率。 ⚫ 由乘法公式可知 ⚫ … … Ai ( ) n P Ai 1 = ( ) n n P Ai −1 = (i =1,2,,n) = = − = n i p P A A A P Ai 1 0 ( 1 2 n ) 1 ( ) ! 1 1 2 3 n P A A A An = ( ) ( ) ( ) ( ) ( i j n) n n P Ai Aj P Ai P Aj Ai − = = 1 1 1 ( ) ( ) ( ) ( )( ) ( i j k n) n n n P Ai Aj Ak P Ai Aj P A Aj A − − = = 1 1 2 1 k i 8/21