
2填空:如果一个函数,在其定义域内,对于自变量的不同取值航 区间,有不同的 ,则称其为分段函数 3做一做:函数gx4,0 x2+1,x≥1的定义域为 2x-1,x≥0则f2+-I- 2)已知函数)尸2-4x,x <0, 解析:)分段函数的定义域是各段自变量取值范围的并集, 所以函数fx)的定义域为(-oo,0)U[1,+oo) (2f2)+f-1)=(2×2-1)+2-4×(-1)1=9. 答案:(1)(-0,0)U[1,+∞)(2)9
导航 2.填空:如果一个函数,在其定义域内,对于自变量的不同取值 区间,有不同的对应方式,则称其为分段函数. 3.做一做:(1)函数 f(x)= 𝒙 𝟐 + 𝟏,𝒙 ≥ 𝟏, 𝟑𝒙-𝟒,𝒙 < 𝟎 的定义域为 . (2)已知函数 f(x)= 𝟐𝒙-𝟏,𝒙 ≥ 𝟎, 𝟐-𝟒𝒙,𝒙 < 𝟎, 则 f(2)+f(-1)= . 解析:(1)分段函数的定义域是各段自变量取值范围的并集, 所以函数f(x)的定义域为(-∞,0)∪[1,+∞). (2)f(2)+f(-1)=(2×2-1)+[2-4×(-1)]=9. 答案:(1)(-∞,0)∪[1,+∞) (2)9

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)分段函数各段上的自变量的取值范围的并集为R(×) (2)分段函数各段上的函数值集合的交集为@.(×) (3)分段函数的图象一定是不连续的.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)分段函数各段上的自变量的取值范围的并集为R.( ) (2)分段函数各段上的函数值集合的交集为⌀.( ) (3)分段函数的图象一定是不连续的.( ) × × ×

导航 课堂·重难突破 探究一分段函数求值问题 【例1】已知函数 x+1,X≤-2, fx)=x2+2x,-2<x<2, 2x-1,x≥2. )求-53)f()的值; (2)若f=3,求实数a的值
导航 课堂 ·重难突破 探究一分段函数求值问题 【例 1 】已知函数 f(x)= 𝒙 + 𝟏,𝒙 ≤ -𝟐, 𝒙𝟐 + 𝟐𝒙,-𝟐 < 𝒙 < 𝟐, 𝟐𝒙-𝟏,𝒙 ≥ 𝟐. (1) 求 f(-5),f(-√ 𝟑),f 𝒇 - 𝟓𝟐 的值; (2) 若 f(a)=3,求实数 a 的值
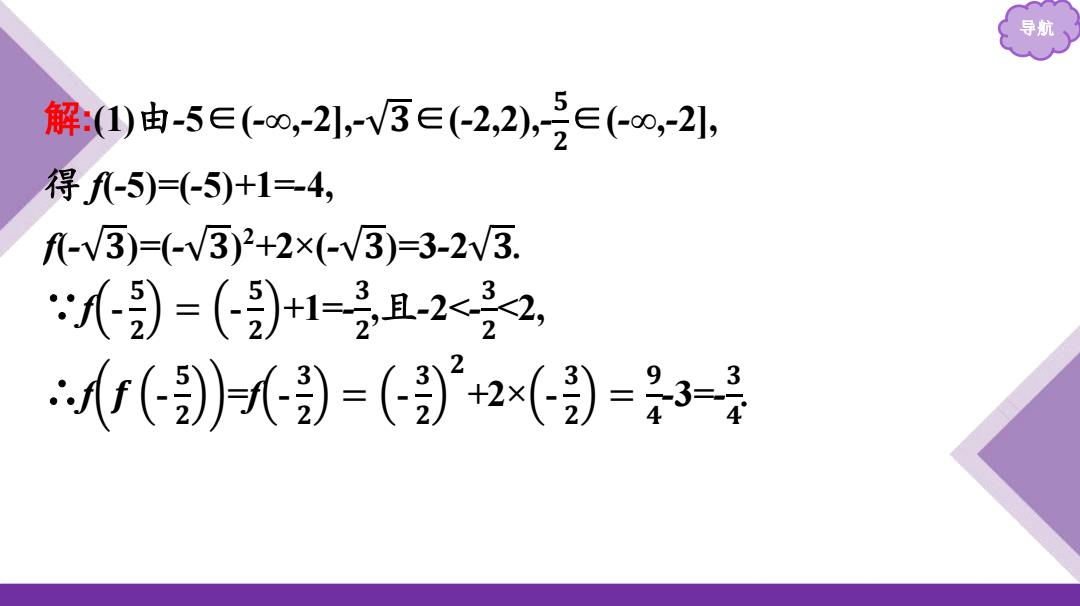
导航 解:(1)由-5∈(0,-2,-V3∈(-2,2),5∈(0,-2, 得-5)=(-5)+1=4, f-V3)=(V3)2+2×(V3)=3-2V3. “(-)=()+1=2且-2×32, f()到=(》+2x(》=3
导航 解:(1)由-5∈(-∞,-2],-√𝟑∈(-2,2),- 𝟓 𝟐 ∈(-∞,-2], 得 f(-5)=(-5)+1=-4, f(-√𝟑)=(-√𝟑) 2 +2×(-√𝟑)=3-2√𝟑. ∵f - 𝟓 𝟐 = - 𝟓 𝟐 +1=- 𝟑 𝟐 ,且-2<- 𝟑 𝟐 <2, ∴f 𝒇 - 𝟓 𝟐 =f - 𝟑 𝟐 = - 𝟑 𝟐 𝟐 +2× - 𝟑 𝟐 = 𝟗 𝟒 -3=- 𝟑 𝟒

导航 2)当≤-2时,a+1=3, 解得=2>-2,不合题意,舍去; 当-2<<2时,2+2a=3, 即2+2a-3=0. 解得=1或a=3. .1∈(-2,2),-3庄(-2,2), ∴.=1符合题意; 当≥2时,2-1=3,解得=2,符合题意. 综上可得,=1或=2
导航 (2) 当 a ≤ - 2 时 ,a+ 1 =3, 解得a= 2 >-2,不合题意 ,舍去 ; 当 - 2<a< 2 时 , a 2 + 2a=3, 即 a 2 + 2 a - 3 = 0 . 解得a= 1 或a=- 3 . ∵ 1 ∈ ( -2,2), - 3 ∉ ( -2,2), ∴a= 1符合题意 ; 当 a ≥ 2 时,2 a - 1 =3,解得a=2,符合题意 . 综上可得 ,a= 1 或a= 2