
定义1-5 设函数f(x)在区间x>a(a)0)上有定义 若当x→0时,函数f(x)无限趋向于某一常 数A,则称函数(x)当x趋于∞时以A为极限 记作Iimf(x)=A或f(x)→A(x→o): r-co 否则,称fx)当x趋于∞时发散, 或 limf(x)不存在. 陶 翻
lim . ( ) ( ) ( ) x f x A f x A x → = → → 或 lim ( ) x f x → 否则,称 f (x) 当x 趋于∞时发散, 或 不存在. 记作 定义1-5 设函数 在区间 上有定义, 若当 时,函数 无限趋向于某一常 数A,则称函数 当x 趋于∞时以A为极限, f (x) x → f (x) f (x) x a(a0)
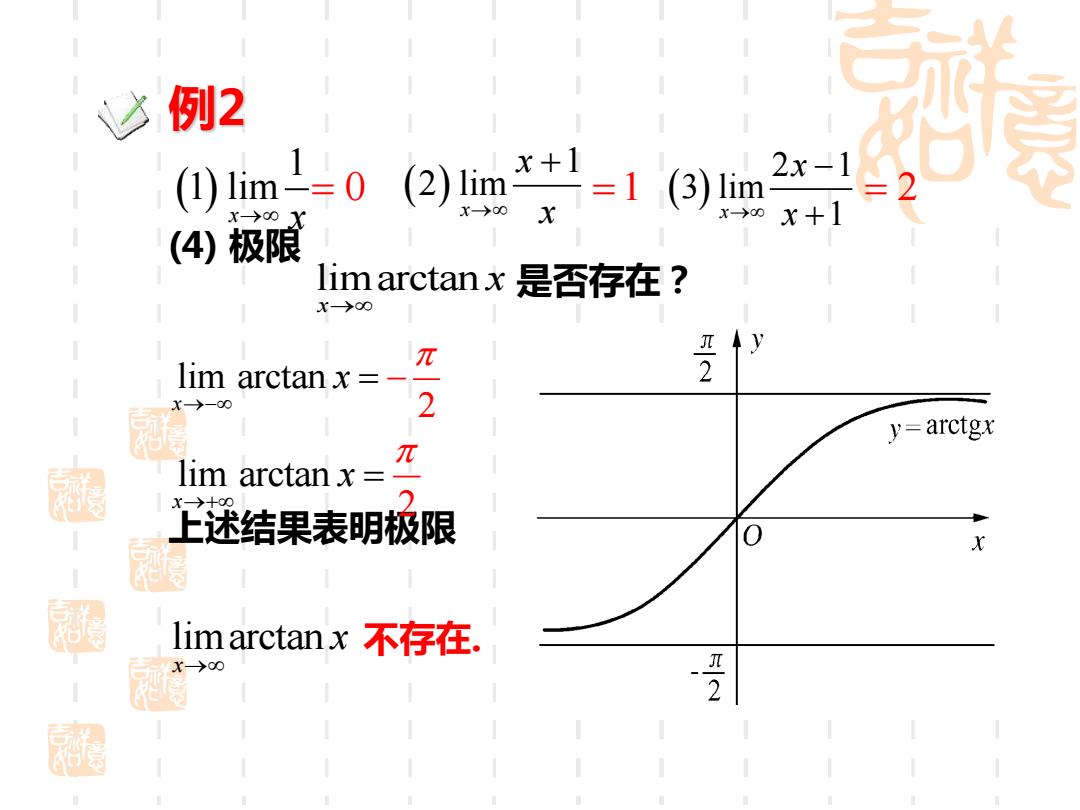
达 例2 002四'-1(- =2 x→0X X (4)极限 limarctanx是否存在? X>0∞ π y lim arctan x=- X-00 2 y=arctgx π lim arctan x 述结果表明极限 0 X limarctanx不存在. X→00 2
( ) 1 2 lim x x → x + ( ) 1 1 lim x→ x ( ) 2 1 3 lim x 1 x → x − + lim arctan x 2 x →− = − limarctan x x → 上述结果表明极限 不存在. lim arctan x 2 x →+ = limarctan x x → (4) 极限 是否存在? 例2 = 0 =1 = 2