
1 lim=0 n→on limg"=0(lq<1) (r lim 2n =+oo n→oo im(-1) n->o0 不存在
1 lim 0 n→ n = lim 0 1 . ( ) n n q q → = 1 lim 1 ( 1) 1 2 n n n→ + − = lim 2 n n → = + ( ) 1 lim 1 n n − → − 不存在

[几点说明] 1.数列的收敛与否与这个数列的增减性无关 常数列一定是收敛数列。limC=C n-→c0 2收敛数列一定有界,但有界数列不一定收敛。 3.收敛数列的轻限有的可以到堕的不能达到。 不存任 例如,常数列可以达到它的极限,但一般数列 都不能达到它们的极限。 im2-0a,-≠0 n-→on n 井
1.数列的收敛与否与这个数列的增减性无关 常数列一定是收敛数列。 # lim n C C → = [几点说明] 2.收敛数列一定有界,但有界数列不一定收敛。 3.收敛数列的极限有的可以达到有的不能达到。 例如,常数列可以达到它的极限,但一般数列 都不能达到它们的极限。 1 lim 0 n→ n = 1 0 n a n = ( ) 1 lim 1 n n − → − 不存在
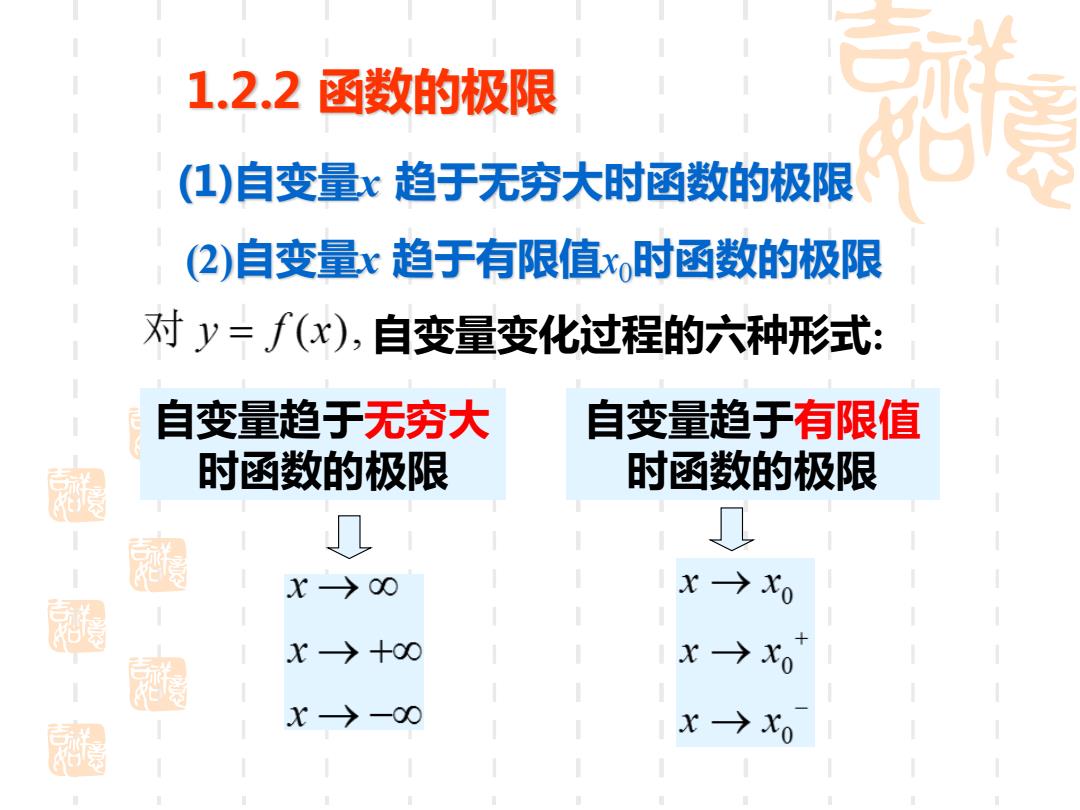
1.2.2函数的极限 (1)自变量x趋于无穷大时函数的极限 (2)自变量x趋于有限值x时函数的极限 对y=∫(x),自变量变化过程的六种形式: 自变量趋于无穷大 自变量趋于有限值 时函数的极限 时函数的极限 涵 X→00 x→x0 X→十00 x→xo X→一00 x→xo
1.2.2 函数的极限 (1)自变量x 趋于无穷大时函数的极限 (2)自变量x 趋于有限值x0时函数的极限 自变量趋于有限值 时函数的极限 自变量变化过程的六种形式: 自变量趋于无穷大 时函数的极限

(1)自变量x趋于无穷大时函数的极限 x→0(x→+0,x→-0) 考察函数 y= x+1 当x的绝对值趋于 履 无穷大时的变化趋势。 涵
(1)自变量x 趋于无穷大时函数的极限 考察函数 x 当x的绝对值趋于 x y +1 = 无穷大时的变化趋势
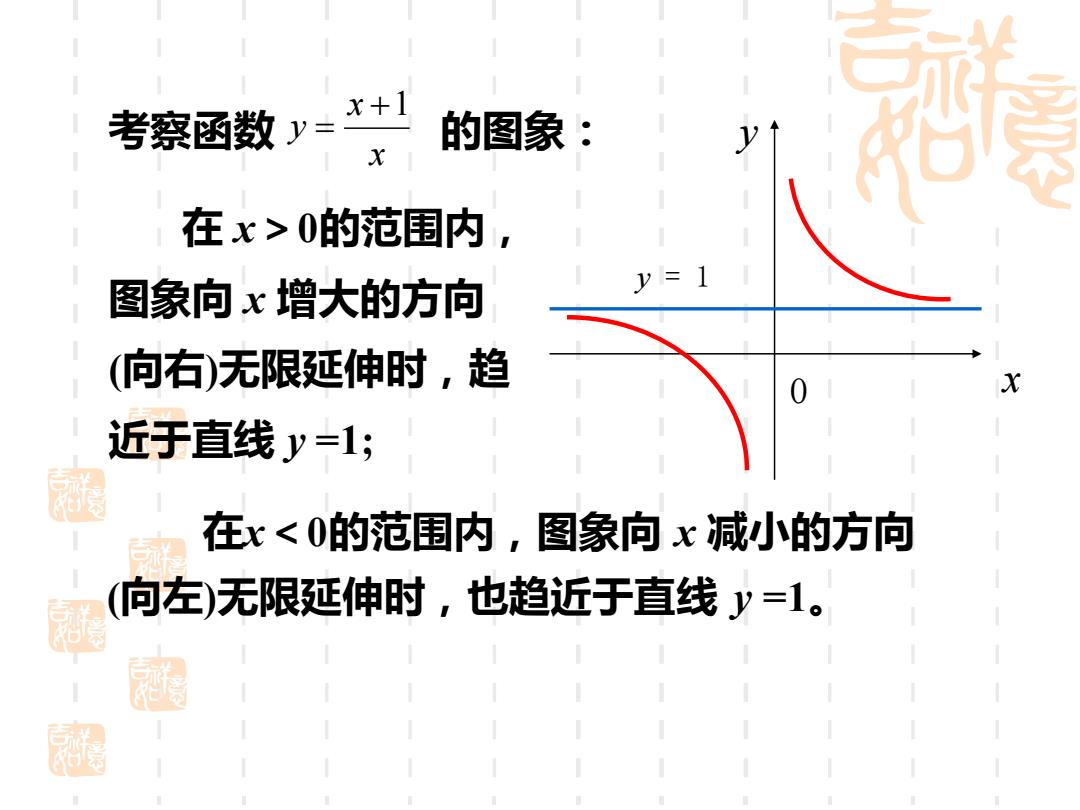
考察函数y-x+1 的图象: X 在x>0的范围内 图象向x增大的方向 y=1 (向右)无限延伸时,趋 x 近于直线y=1; 湿 在x<0的范围内,图象向x减小的方向 向左)无限延伸时,也趋近于直线y=1
在x<0的范围内,图象向 x 减小的方向 (向左)无限延伸时,也趋近于直线 y =1。 考察函数 x x y +1 = 的图象: y x y = 1 0 在 x>0的范围内, 图象向 x 增大的方向 (向右)无限延伸时,趋 近于直线 y =1;