《线性代数》课程教学课件（讲稿，B）§3.4 分块矩阵

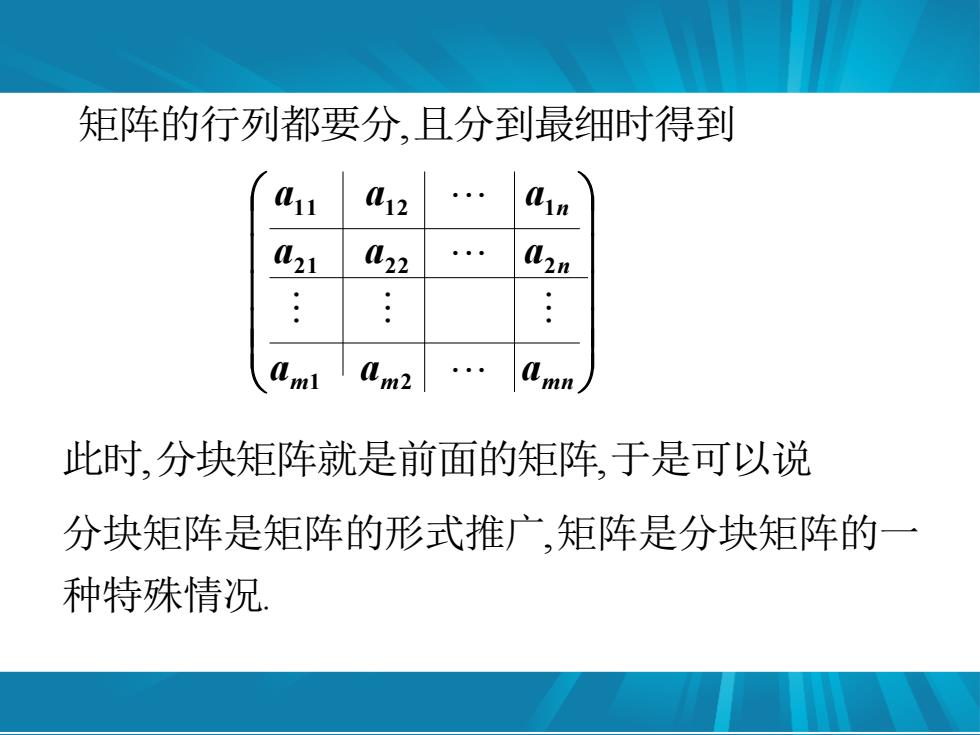
矩阵的行列都要分，且分到最细时得到 11 12 421 422 。 .: Ami am2 此时，分块矩阵就是前面的矩阵，于是可以说 分块矩阵是矩阵的形式推广，矩阵是分块矩阵的一 种特殊情况

              m m m n n n a a a a a a a a a       1 2 2 1 2 2 2 1 1 1 2 1 矩阵的行列都要分,且分到最细时得到 此时,分块矩阵就是前面的矩阵,于是可以说 . , 种特殊情况 分块矩阵是矩阵的形式推广 矩阵是分块矩阵的一

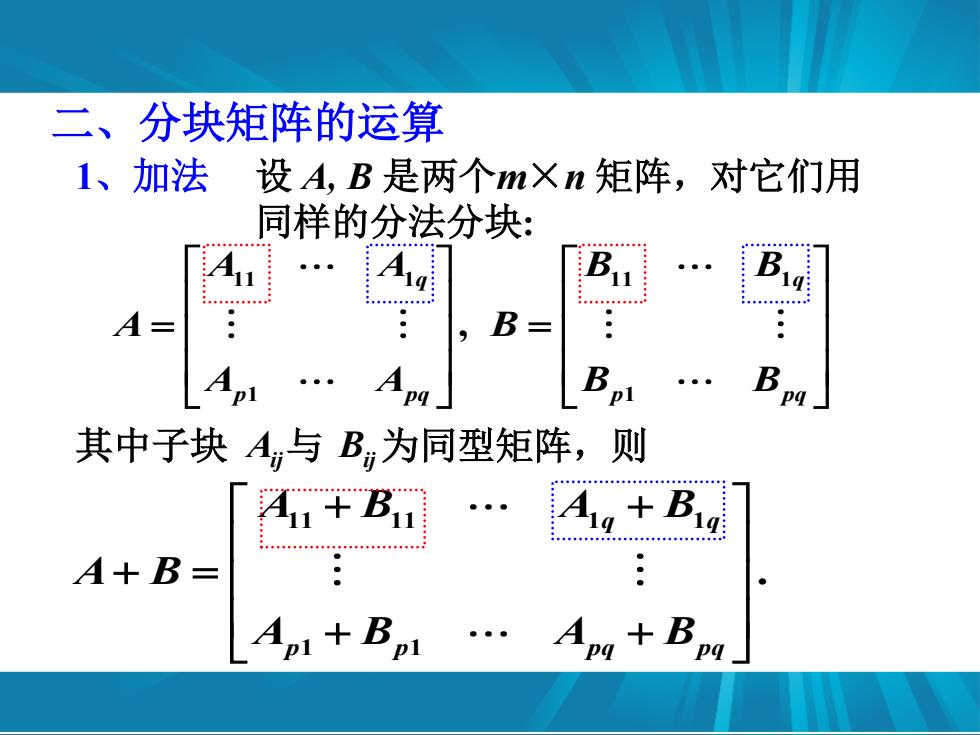
二、分块矩阵的运算 1、加法 设A,B是两个m义n矩阵，对它们用 同样的分法分块： A A=: 品A人 B= 其中子块A,与B为同型矩阵，则 1+B 4+B : A1+BpApg+Bpm

11 1 11 1 1 1 , q q p pq p pq A A B B A B A A B B                       1、加法 设 A, B 是两个m×n 矩阵，对它们用 同样的分法分块: 二、分块矩阵的运算 11 11 1 1 1 1 . q q p p pq pq A B A B A B A B A B                 其中子块 Aij 与 Bij 为同型矩阵，则

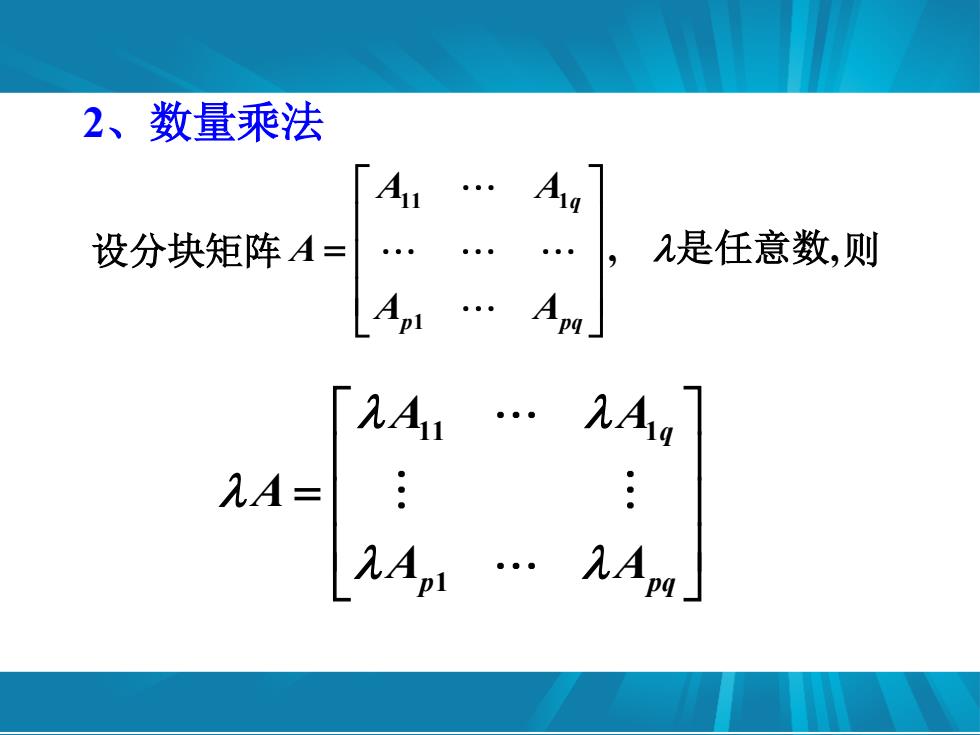
2、数量乘法 设分块矩阵A= 2是任意数，则 λA=

2、数量乘法 设分块矩阵 11 1 1 , , q p pq A A A A A             是任意数 则 11 1 1 q p pq A A A A A                

3、乘法 把矩阵A=(ax)x,B=(b)xp分块成 「A· A B1.B1g 及4 其中A1,A2,.,A的列数分别等于Bj3B2j)., B的行数，那末 C1 AB= 其中Cg=∑AwBg(i=1,.,pj=1,）

11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B                       其中 的列数分别等于 的行数 那末   11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q             其中     3、乘法 把矩阵 ( ) , ( ) A a B b   ik m s kj s p   分块成

说明： 1当左边分块矩阵的列的分块方法和右边分块矩阵的分 块方法相同时，两个分块矩阵才可以相乘 2.两个分块矩阵的乘积仍是分块矩阵，并且乘积分块矩 阵的行数等于左边分块矩阵的行数，乘积分块矩阵的列 数等于右边分块矩阵的列数 3.分块矩阵的第行第列子块C等于左边分块矩阵的第 行与右边分块矩阵第列的对应子块乘积之和 Ci=AnBy++Aip Bpi

Cij  Ai1 B1 j  AipBp j 说明: , . 1. 块方法相同时 两个分块矩阵才可以相乘 当左边分块矩阵的列的分块方法和右边分块矩阵的分 . , 2. , 数等于右边分块矩阵的列数 阵的行数等于左边分块矩阵的行数 乘积分块矩阵的列 两个分块矩阵的乘积仍是分块矩阵 并且乘积分块矩 . 3. 行与右边分块矩阵第 列的对应子块乘积之和 分块矩阵的第 行第 列子块 等于左边分块矩阵的第 i j i j Cij