西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第四章 时变电磁场

合KA#apW.A=-u8洛仑兹条件Ot0-A72A--UJOt?达朗贝尔方程（DalangbaierEguation）apP7p-at-这是非齐次波动方程T讨论与引伸1）洛仑兹条件（Luo lunciCondition）的重要意义确定了 V·A 的值，与B=V×A 共同唯一确定A;·简化了动态位与场源之间的关系，使得A单独由J决定，单独由r决定，给解题带来了方便：洛仑兹条件是电流连续性原理的体现。2）若场不随时间变化，波动方程蜕变为泊松方程V'p=-p/V’A=-W

 A  J 2 2) 若场不随时间变化，波动方程蜕变为泊松方程 • 简化了动态位与场源之间的关系，使得A单独由J决定，j单独由r决定， 给解题带来了方便； • 洛仑兹条件是电流连续性原理的体现。 1） 洛仑兹条件（Luo lunci Condition)的重要意义     /  2 这是非齐次波动方程 达朗贝尔方程 (Dalangbaier Eguation)                    2 2 2 2 2 2 t t J A A t       A  洛仑兹条件 • 确定了  A 的值，与 B   A 共同唯一确定A；

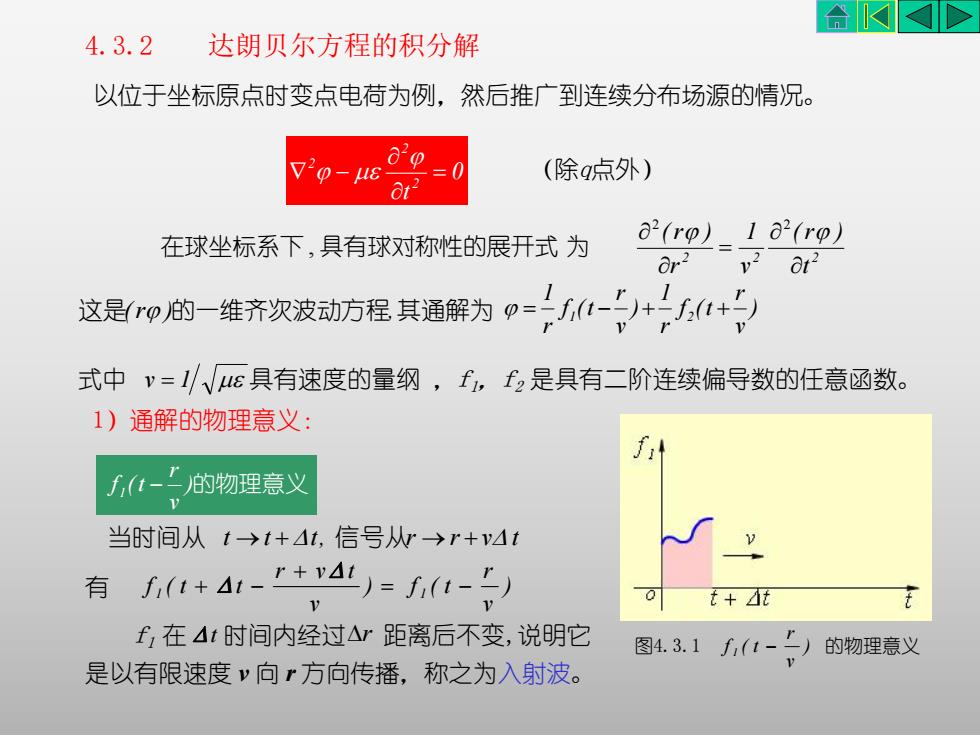
AD4.3.2达朗贝尔方程的积分解以位于坐标原点时变点电荷为例，然后推广到连续分布场源的情况。ap（除q点外）=0-at?a?(rp).1 a?(rp)在球坐标系下，具有球对称性的展开式为ar22at这是(rg)的一维齐次波动方程其通解为 =f(t-)+=f(t+)式中v=l/us具有速度的量纲，fi，fz是具有二阶连续偏导数的任意函数。1）通解的物理意义Jitf(t--的物理意义当时间从t→t+At，信号从r→r+么t有 J(141-+)= J(1-0tt+Atfi在4t时间内经过△r距离后不变，说明它图4.3.1f（t-=）的物理意义是以有限速度向方向传播，称之为入射波

4.3.2 达朗贝尔方程的积分解 以位于坐标原点时变点电荷为例，然后推广到连续分布场源的情况。 0 t 2 2 2         2 2 2 t (r ) v 1 r (r )        2 2 在球坐标系下 , 具有球对称性的展开式 为 ) v r f (t r 1 ) v r f (t r 1   1   2  1）通解的物理意义： )的物理意义 v r f (t 1  当时间从 t t  t, 信号从r  r  v t f1 在 时间内经过 距离后不变,说明它 是以有限速度 v 向 r 方向传播，称之为入射波。  t r 这是(r )的一维齐次波动方程,其通解为 式中 v  1  具有速度的量纲 ，f1，f2 是具有二阶连续偏导数的任意函数。 （除q点外） ) v r ) f ( t v r v t f ( t t 1  1      有  图4.3.1 ) 的物理意义 v r f ( t 1 

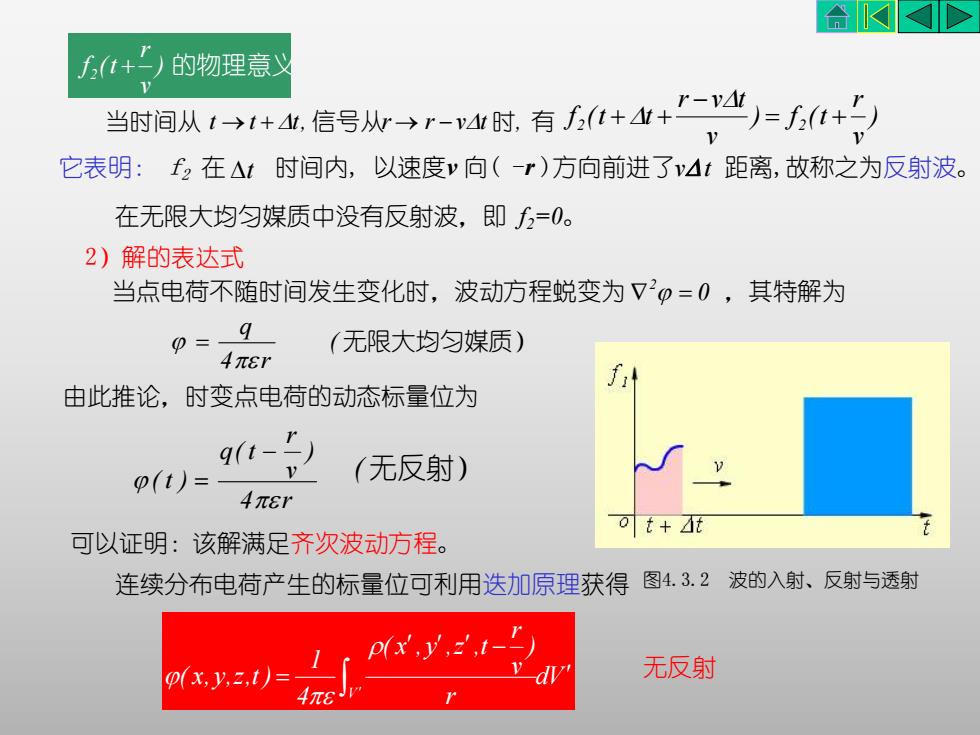
合KAf(t+-)的物理意义当时间从 1→I+4,信号从→r-v4时, 有 (1+4+V)=f(1+1它表明：f，在△t时间内，以速度v向（-r）方向前进了v△t距离，故称之为反射波在无限大均匀媒质中没有反射波，即f=0。2）解的表达式当点电荷不随时间发生变化时，波动方程蜕变为√=0，其特解为0=q（无限大均匀媒质）4元rJit由此推论，时变点电荷的动态标量位为q(t-（无反射）1@(t)=4元ot+Zt可以证明：该解满足齐次波动方程连续分布电荷产生的标量位可利用选加原理获得图4.3.2波的入射、反射与透射p(x,y,=,t-无反射dyp(x,y,z,t)=4元

) 的物理意义 v r f (t 2  当时间从 t t  t, 信号从r r vt 时, 有 ) v r ) f (t v r v t f (t t 2  2       ( 无限大均匀媒质） 4 r q    由此推论，时变点电荷的动态标量位为 可以证明：该解满足齐次波动方程。 在无限大均匀媒质中没有反射波，即 f2=0。 它表明： f2 在 t 时间内, 以速度v 向( -r )方向前进了vt 距离,故称之为反射波。 4 r ) v r q( t ( t )     ( 无反射） 2）解的表达式 连续分布电荷产生的标量位可利用迭加原理获得 dV r ) v r ( x , y ,z ,t 4 1 ( x, y,z,t ) V            无反射 图4.3.2 波的入射、反射与透射 当点电荷不随时间发生变化时，波动方程蜕变为  2  0 ，其特解为

AD若激励源是时变电流源时，仿上述方法推导，得到A的表达式J(xy,zt-r)（无反射）A(x,y,z,t)=H[ydv4元1当场源不随时间变化时，蜕变为恒定磁场中的磁失位A。讨论与引伸·达朗贝尔方程解的形式表明：t时刻的响应取决于(1--）时刻激励源的情况。故又称A、为滞后位（RetardedPotential）。·电磁波是以有限速度传播的，这个速度称为波速v=lusm/s·电磁波在真空中的波速与光速相等。光也是一种电磁波。为何将达朗贝尔方程中的v=1/us定义为速度？·它具有速度的量纲；且通解中的f（t-一）经过么后得以保持不变，必有自dr变量不变, 即 t-二= const → r=v(t-const)→=Vdt它表明：f是一个以速度沿方向前进的波

当场源不随时间变化时，蜕变为恒定磁场中的磁矢位A。 • 电磁波在真空中的波速与光速相等。光也是一种电磁波。 为何将达朗贝尔方程中 的v  1  定义为速度 ? • 达朗贝尔方程解的形式表明：t 时刻的响应取决于 时刻激励源的情况。 故又称 A、 为滞后位（Retarded Potential）。 ) v r (t   它表明： f1是一个以速度 v 沿 r方向前进的波。 若激励源是时变电流源时，仿上述方法推导，得到A的表达式 dV r ) v r ( x , y ,z ,t 4 ( x, y,z,t ) V         J A   （无反射） • 电磁波是以有限速度传播的，这个速度称为波速 v1  m/s • 它具有速度的量纲；且通解中的 经过 后得以保持不变，必有自 变量不变，即 v dt dr const r v(t const ) v r t        ) v r f (t 1  t 

KD4.4：坡印亭定理和坡印亭失量·电磁能量符合自然界物质运动过程中能量守恒和转化定律一一坡印亭定理：·坡印亭矢量是描述电磁场能量流动的物理量。4.4.1#坡印亭定理（PoyntingTheorem）在时变场中，电、磁能量相互依存，总能量密度为w=w+wm=-D.E+-B.H22W =J, wdV= J(D.E+B.H)dv体积V内储存的能量为设体积元储存能量wdV随时间的变化率为a(wdV)_[(D.E+B·H)dvatatl22D+H.)dV=[E-(V×H-J)-H:(VE)v=(E.0at+Hat利用矢量恒等式V（E×H）=H·（VxE）-E·（V×H）(wdV)-[(V(E×H)+E-J)v则有at取体积分，得.wdV=-f,(ExH).ds-E.JdvtJ

4.4 坡印亭定理和坡印亭矢量 • 电磁能量符合自然界物质运动过程中能量守恒和转化定律——坡印亭定理； • 坡印亭矢量是描述电磁场能量流动的物理量。 4.4.1 坡印亭定理（Poynting Theorem） 在时变场中，电、磁能量相互依存，总能量密度为    DE  BH 2 1 2 1 w we wm               )dV 2 1 2 1 ( t t ( wdV ) wdV D E B H 设体积元储存能量 随时间的变化率为 )dV  ( ) ( )dV t t ( E H J H E B H D E                利用矢量恒等式 (EH ) H(E)E(H ) dV 2 1 V W wdV V V 体积 内储存的能量为   （D E  B H） ( ( ) )dV t (wdV )    EH  EJ   则有 取体积分，得            V S V wdV ( ) d dV t E H S E J